ECC圆锥曲线

简介概括

非对称加密算法—ECC加密算法

椭圆曲线密码学(Elliptic Curve Cryptography,缩写:ECC)是一种基于椭圆曲线数学的公开密钥加密算法

ECC的主要优势是它相比RSA加密算法使用较小的密钥长度并提供相当等级的安全性,ECC的另一个优势是可以定义群之间的双线性映射,基于Weil对或是Tate对;双线性映射已经在密码学中发现了大量的应用,例如基于身份的加密

原理解释

1.基础概念

1.1椭圆曲线

椭圆曲线是一种特殊的数学曲线,其方程通常表示为:y^2=x^3+ax+b

为了确保这个方程表示的曲线没有奇点(即曲线是平滑的,没有自交点或尖点),需要满足一个特定的条件,这个条件是通过计算曲线的判别式得到的,对于椭圆曲线y^2=x^3+ax+b,其判别式Δ为:Δ=-16(4a^3+27b^2)

为了使曲线没有奇点,判别式Δ必须不等于零;因此,我们有:-16(4a^3+27b^2<sup></sup>)≠0

由于-16是一个非零常数,所以这个条件可以简化为:4a^3<sup></sup>+27b^2≠0以确保曲线是平滑的,没有奇点

1.2椭圆曲线上的点

椭圆曲线上的点P是满足上述方程的坐标(x,y),此外,还定义了一个无穷远点O,它在椭圆曲线的加法运算中起到零元的作用

• 对于椭圆曲线上的任意点P,有:P+O=O+P=P
• 无穷远点O是椭圆曲线加法群的单位元

对于阶的定义

• 如果椭圆曲线上一点P,存在最小的正整数n使得数乘nP=0∞,则将n称为P的阶;若n不存在,则P是无限阶的
• 简单来说阶表示了从基点G开始,通过不断加法运算,最终回到无穷远点O所需的步数

1.3椭圆曲线的加法运算

椭圆曲线上的点可以通过几何方法进行加法运算,具体规则如下

• 点加:对于两个不同的点P和Q,如果它们不共线,则它们的和R=P+Q是通过P和Q的直线与椭圆曲线的第三个交点的对称点
• 倍点:如果P=Q,则2P是通过P的切线与椭圆曲线的交点的对称点
• 无穷远点:任何点P与无穷远点O的和仍然是P,即P+O=P

1.4椭圆曲线离散对数问题(ECDLP)

椭圆曲线密码算法的安全性基于椭圆曲线离散对数问题的计算困难性,给定椭圆曲线上的点G和P,已知P=kG(其中k是一个正整数),求解k是关键

(后续题目涉及该思想)

2.ECC加密过程

2.1密钥生成

1.选择椭圆曲线参数

• 选择一个椭圆曲线E,其方程为y^2=x^3+ax+b
• 选择一个基点G,它是椭圆曲线上的一个生成元,其阶为n(即nG=O)

2.生成私钥和公钥

• 私钥:随机选择一个整数d(私钥),满足1<d<n
• 公钥:计算Q=dG,其中Q是公钥

2.2加密过程

假设A要向B发送消息M,B的公钥为Q<sub>B</sub>,其基点为G,则加密过程如下

1.选择随机数

• A随机选择一个整数k,满足1<k<n

2.计算椭圆曲线点

• 计算C1=kG
• 计算C2=M+kQB,其中M是消息点(需要将消息映射到椭圆曲线上的一个点)

3.发送密文

• A将密文(C1,C2)发送给B

2.3解密过程

B收到密文(C1,C2)后,解密过程如下

1.计算共享密钥点

• B使用自己的私钥d<sub>B</sub>,计算d<sub>B</sub>C1=d<sub>B</sub>(kG)=k(d<sub>B</sub>G)=kQB

2.恢复消息点

• 由于C2=M+kQB,B可以通过M=C2-kQB恢复消息点M

3.示例

import numpy as np
import matplotlib.pyplot as plt
import matplotlib

# 设置 Matplotlib 使用支持中文的字体
matplotlib.rcParams['font.family'] = 'SimHei'  # 或 'Microsoft YaHei'
matplotlib.rcParams['font.size'] = 12
matplotlib.rcParams['axes.unicode_minus'] = False  # 正确显示负号


# 定义椭圆曲线方程
def elliptic_curve(x, a, b, p):
    return (x ** 3 + a * x + b) % p


# 椭圆曲线上的点加法
def point_addition(P, Q, a, p):
    if P == Q:
        # 计算切线斜率
        lam = (3 * P[0] ** 2 + a) * pow(2 * P[1], -1, p) % p
    else:
        # 计算割线斜率
        lam = (Q[1] - P[1]) * pow(Q[0] - P[0], -1, p) % p

    x3 = (lam ** 2 - P[0] - Q[0]) % p
    y3 = (lam * (P[0] - x3) - P[1]) % p
    return (x3, y3)


# 椭圆曲线参数
a = 2
b = 2
p = 23  # 有限域模数
G = (16, 5)  # 基点
n = 19  # 基点的阶

# 计算倍点
points = [G]
for i in range(2, n):
    points.append(point_addition(points[-1], G, a, p))

# 绘制椭圆曲线
x = np.linspace(-3, 20, 400)
y = np.sqrt(elliptic_curve(x, a, b, p))

plt.figure(figsize=(10, 6))
plt.plot(x, y, label='y^2 = x^3 + 2x + 2 (mod 23)', color='blue')
plt.plot(x, -y, label='y^2 = x^3 + 2x + 2 (mod 23)', color='blue')

# 绘制点
for i, point in enumerate(points):
    plt.scatter(point[0], point[1], color='green', s=50, zorder=5)
    plt.text(point[0], point[1], f'{i + 1}G', fontsize=10, ha='right')

# 标记基点 G
plt.scatter(G[0], G[1], color='red', s=100, zorder=5)
plt.text(G[0], G[1], 'G (16, 5)', fontsize=12, ha='right')

# 标记无穷远点 O
plt.scatter([], [], color='black', s=100, zorder=5)
plt.text(0, 0, 'O (无穷远点)', fontsize=12, ha='right')

# 设置图形属性
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid(color='gray', linestyle='--', linewidth=0.5)
plt.title('椭圆曲线：y^2 = x^3 + 2x + 2 (mod 23)')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.xlim(-3, 20)
plt.ylim(-20, 20)

# 显示图形
plt.show()

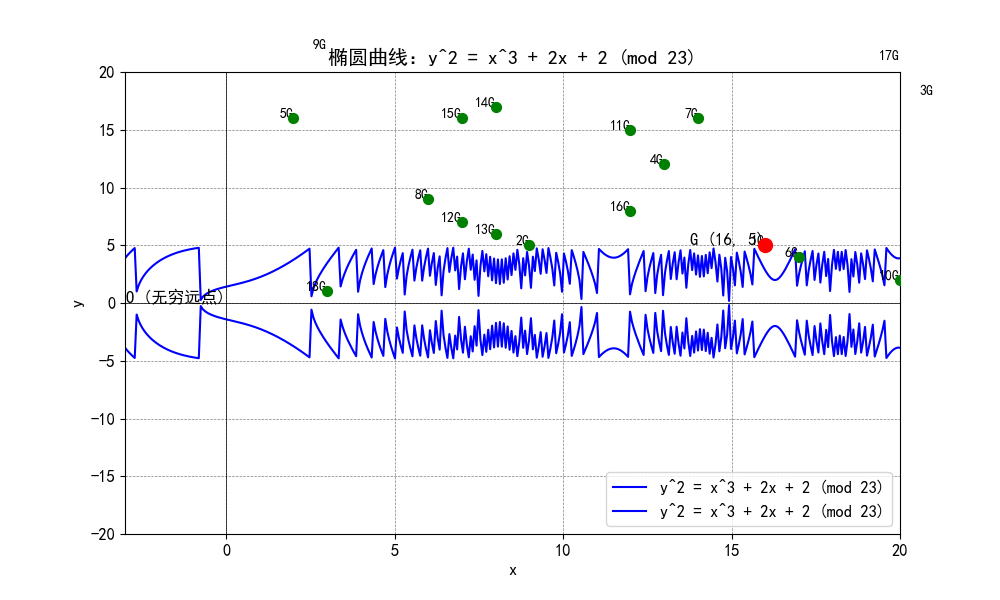
假设椭圆曲线方程为y^2=x^3+2x+2,基点G=(16,5),阶n=19,有限域模数p=23

3.1密钥生成

1.选择参数

• 选择椭圆曲线方程y^2≡x^3+2x+2 (mod 23)
• 选择基点G=(16,5),其阶为n=19
• 选择有限域模数p=23

2.生成私钥和公钥

• 私钥:随机选择一个整数d,满足1<d<n,例如,假设d=7
• 公钥:计算Q=dG,具体计算过程如下
  • 2G=(5,1)
  • 4G=(6,15)
  • 6G=(10,6)
  • 7G=(3,1)
  • 因此公钥Q=(3,1)

3.2加密过程

假设A要向B发送消息M,B的公钥为QB=(3,1),其基点为G=(16,5),模数为p=23,则加密过程如下

1.选择随机数

• A随机选择一个整数k,满足1<k<n,假设k=3

2.计算椭圆曲线点

• 计算C1=kG=3(16,5)

  • 2G=(5,1)
  • 3G=(10,6)
  • 因此C1=(10,6)

• 计算C2=M+kQB,假设消息M=(13,7)

  • kQB=3(3,1)
  • 2(3,1)=(16,5)
  • 3(3,1)=(10,6)
  • 因此C2=(13,7)+(10,6)
  • 计算(13,7)+(10,6)

  

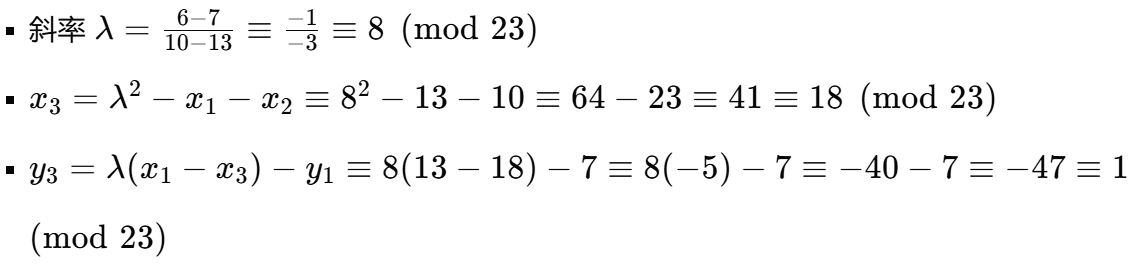
  • 因此C2=(18,1)

3.发送密文

• A将密文(C1,C2)=((10,6),(18,1))发送给B

3.3解密过程

B收到密文(C1,C2)=((10,6),(18,1))后,解密过程如下

1.计算共享密钥点

B使用自己的私钥d<sub>B</sub>=7,计算d<sub>B</sub>C1=7(10,6)

• 2(10,6)=(10,17)
• 4(10,6)=(10,6)
• 6(10,6)=(10,17)
• 7(10,6)=(3,22)
• 因此d<sub>B</sub>C1=(3,22)

2.恢复消息点

计算M=C2-kQB

• C2-kQB=(18,1)-(10,6)

• 计算(18,1)-(10,6)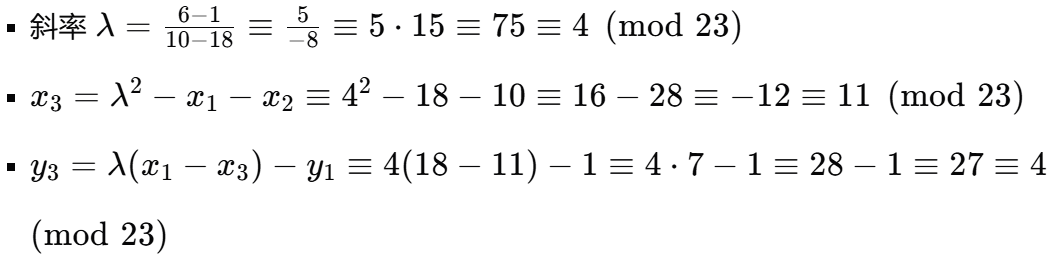

  

  • 因此M=(13,7)

发展历史

初创阶段

• 1985年:ECC由Neal Koblitz和Victor Miller分别独立提出,他们基于椭圆曲线的数学特性,尤其是椭圆曲线离散对数问题的计算困难性,设计了这种加密算法

发展阶段

• 20世纪90年代至21世纪初:ECC逐渐受到密码学界的关注,由于其在相同安全级别下所需的密钥长度更短,计算效率更高,开始在一些对安全性和效率要求较高的领域得到应用
• 2004年:ECC算法开始普遍使用

应用与推广阶段

• 2005年:美国国家标准与技术研究院(NIST)将ECC纳入其密码学标准
• 2008年:比特币诞生,其加密算法采用了ECC,进一步推动了ECC在数字货币领域的应用
• 2016年:研究人员使用FPGA实现并行Pollard`s rho算法,破解了117.35位的通用椭圆曲线离散对数

现代阶段

• ECC已成为现代密码学的重要组成部分,广泛应用于数字签名(如ECDSA),密钥交换(如ECDH)等领域
• 随着物联网,移动支付等新兴技术的发展,ECC因其高效性和安全性,逐渐成为这些领域的首选加密算法