牛顿恒等式

题目:

from secret import flag

assert flag[:6] == 'TPCTF{' and flag[-1] == '}'
flag = flag[6:-1]

assert len(set(flag)) == len(flag)

xs = []
for i, c in enumerate(flag):
    xs += [ord(c)] * (i + 1)

p = 257
print('output =', [sum(pow(x, k, p) for x in xs) % p for k in range(1, len(xs) + 1)])
#output = [125, 31, 116, 106, 193, 7, 38, 194, 186, 33, 180, 189, 53, 126, 134, 237, 123, 65, 179, 196, 99, 74, 101, 153, 84, 74, 233, 5, 105, 32, 75, 168, 161, 2, 147, 18, 68, 68, 162, 21, 94, 194, 249, 179, 24, 60, 71, 12, 40, 198, 79, 92, 44, 72, 189, 236, 244, 151, 56, 93, 195, 121, 211, 26, 73, 240, 76, 70, 133, 186, 165, 48, 31, 39, 3, 219, 96, 14, 166, 139, 24, 206, 93, 250, 79, 246, 256, 199, 198, 131, 34, 192, 173, 35, 0, 171, 160, 151, 118, 24, 10, 100, 93, 19, 101, 15, 190, 74, 10, 117, 4, 41, 135, 45, 107, 155, 152, 95, 222, 214, 174, 139, 117, 211, 224, 120, 219, 250, 1, 110, 225, 196, 105, 96, 52, 231, 59, 70, 95, 56, 58, 248, 171, 16, 251, 165, 54, 4, 211, 60, 210, 158, 45, 96, 105, 116, 30, 239, 96, 37, 175, 254, 157, 26, 151, 141, 43, 110, 227, 199, 223, 135, 162, 112, 4, 45, 66, 228, 162, 238, 165, 158, 27, 18, 76, 36, 237, 107, 84, 57, 233, 96, 72, 6, 114, 44, 119, 174, 59, 82, 202, 26, 216, 35, 55, 159, 113, 98, 4, 74, 2, 128, 34, 180, 191, 8, 101, 169, 157, 120, 254, 158, 97, 227, 79, 151, 167, 64, 195, 42, 250, 207, 213, 238, 199, 111, 149, 18, 194, 240, 53, 130, 3, 188, 41, 100, 255, 158, 21, 189, 19, 214, 127]

解题思路:

牛顿恒等式的核心思想

牛顿恒等式可以将幂和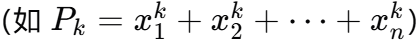与多项式的系数联系起来,具体来说,对于一个多项式的根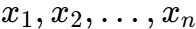,牛顿恒等式可以递归地表示这些幂和

如何利用牛顿恒等式解密

确定多项式的系数:

• 在你的加密过程中,xs列表是由flag的字符ASCII值重复构造的,而output列表是这些值的幂和模257的结果
• 根据牛顿恒等式,可以通过已知的幂和(即output列表)反推出多项式的系数

递归求解初等对称多项式:

• 利用牛顿恒等式,可以从已知的幂和(P_k)递归求解初等对称多项式(e_k),这些对称多项式与多项式的系数直接相关

恢复原始字符:

• 通过初等对称多项式,可以构造出多项式的系数,进而恢复出原始的flag字符串

具体步骤

确定flag的长度:

• 从output的长度可以推断出flag的长度,因为output的长度与xs的构造方式有关

利用牛顿恒等式递归求解:

• 根据牛顿恒等式,从已知的幂和 (P_k) 开始，逐步求解初等对称多项式(e_k),最终恢复出多项式的系数

逆向构造flag:

• 通过多项式的系数,结合xs的构造方式(字符ASCII值的重复),逐步逆向恢复出flag的每个字符

解答:

output = [125, 31, 116, 106, 193, 7, 38, 194, 186, 33, 180, 189, 53, 126, 134, 237, 123, 65, 179, 196, 99, 74, 101, 153, 84, 74, 233, 5, 105, 32, 75, 168, 161, 2, 147, 18, 68, 68, 162, 21, 94, 194, 249, 179, 24, 60, 71, 12, 40, 198, 79, 92, 44, 72, 189, 236, 244, 151, 56, 93, 195, 121, 211, 26, 73, 240, 76, 70, 133, 186, 165, 48, 31, 39, 3, 219, 96, 14, 166, 139, 24, 206, 93, 250, 79, 246, 256, 199, 198, 131, 34, 192, 173, 35, 0, 171, 160, 151, 118, 24, 10, 100, 93, 19, 101, 15, 190, 74, 10, 117, 4, 41, 135, 45, 107, 155, 152, 95, 222, 214, 174, 139, 117, 211, 224, 120, 219, 250, 1, 110, 225, 196, 105, 96, 52, 231, 59, 70, 95, 56, 58, 248, 171, 16, 251, 165, 54, 4, 211, 60, 210, 158, 45, 96, 105, 116, 30, 239, 96, 37, 175, 254, 157, 26, 151, 141, 43, 110, 227, 199, 223, 135, 162, 112, 4, 45, 66, 228, 162, 238, 165, 158, 27, 18, 76, 36, 237, 107, 84, 57, 233, 96, 72, 6, 114, 44, 119, 174, 59, 82, 202, 26, 216, 35, 55, 159, 113, 98, 4, 74, 2, 128, 34, 180, 191, 8, 101, 169, 157, 120, 254, 158, 97, 227, 79, 151, 167, 64, 195, 42, 250, 207, 213, 238, 199, 111, 149, 18, 194, 240, 53, 130, 3, 188, 41, 100, 255, 158, 21, 189, 19, 214, 127]
p = 257
P = output

e = []
#get e
for i in range(253):
    temp = 0
    for j in range(i):
        temp += (-1)**j * e[j] * P[i-j-1]
        temp %= p
    
    temp = (P[i] - temp) % p
    ei = temp * inverse_mod((-1)^i*(i+1), p) % p
    e.append(ei)

#get a
a = [1]
for i in range(len(e)):
    a.append((-1)^(i+1) * e[i] % p)

#find roots
PR.<x> = PolynomialRing(Zmod(p))
f = 0
for i in range(253):
    f += x^(253-i)*a[i]
f += a[-1]
res = f.roots()

#get flag
flag = [0 for i in range(22)]
for i in res:
    flag[i[1]-1] = chr(i[0])
print("TPCTF{" + "".join(flag) + "}")
#TPCTF{polyisfun_MJCQz:a^VX"G}