对私钥x的攻击
对私钥x的攻击本质上是解决一个**DLP**问题
让G为一个阿贝尔群(交换群),我们把G中的二元操作写成乘法*
1.给定G,g和h=g<sup>a</sup>,计算a是困难的
2.这里a就叫做h的以g为底的离散对数
题目:
利用如下的参数,恢复DSA的秘密钥x
p = 800000000000000089e1855218a0e7dac38136ffafa72eda7859f2171e25e65eac698c1702578b07dc2a1076da241c76c62d374d8389ea5aeffd3226a0530cc565f3bf6b50929139ebeac04f48c3c84afb796d61e5a4f9a8fda812ab59494232c7d2b4deb50aa18ee9e132bfa85ac4374d7f9091abc3d015efc871a584471bb1
q = f4f47f05794b256174bba6e9b396a7707e563c5b
g = 5958c9d3898b224b12672c0b98e06c60df923cb8bc999d119458fef538b8fa4046c8db53039db620c094c9fa077ef389b5322a559946a71903f990f1f7e0e025e2d7f7cf494aff1a0470f5b64c36b625a097f1651fe775323556fe00b3608c887892878480e99041be601a62166ca6894bdd41a7054ec89f756ba9fc95302291
y = 84ad4719d044495496a3201c8ff484feb45b962e7302e56a392aee4abab3e4bdebf2955b4736012f21a08084056b19bcd7fee56048e004e44984e2f411788efdc837a0d2e5abb7b555039fd243ac01f0fb2ed1dec568280ce678e931868d23eb095fde9d3779191b8c0299d6e07bbb283e6633451e535c45513b2d33c99ea17
被签名的消息为:So be friendly, a matter of life and death, just like a etch-a-sketch,它的SHA1值为(十六进制):0xd2d0714f014a9784047eaeccf956520045c45265
得到的签名为:
r = 548099063082341131477253921760299949438196259240
s = 857042759984254168557880549501802188789837994940
已知签名用的"k" 的范围是0到2^16
请编程恢复DSA的秘密钥x,它的SHA1值为:0954edd5e0afe5542a4adf012611a91912a3ec16
思路:
假如这里的p和q都比较小的话,我们可以通过BSGS(大步小步法)来进行简单的攻击
BSGS用于求解离散对数问题,其时间复杂度为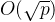
,空间复杂度为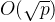
其核心思想是:
from gmpy2 import *
p = mpz('0x800000000000000089e1855218a0e7dac38136ffafa72eda7859f2171e25e65eac698c1702578b07dc2a1076da241c76c62d374d8389ea5aeffd3226a0530cc565f3bf6b50929139ebeac04f48c3c84afb796d61e5a4f9a8fda812ab59494232c7d2b4deb50aa18ee9e132bfa85ac4374d7f9091abc3d015efc871a584471bb1')
g = mpz('0x5958c9d3898b224b12672c0b98e06c60df923cb8bc999d119458fef538b8fa4046c8db53039db620c094c9fa077ef389b5322a559946a71903f990f1f7e0e025e2d7f7cf494aff1a0470f5b64c36b625a097f1651fe775323556fe00b3608c887892878480e99041be601a62166ca6894bdd41a7054ec89f756ba9fc95302291')
y = mpz('0x84ad4719d044495496a3201c8ff484feb45b962e7302e56a392aee4abab3e4bdebf2955b4736012f21a08084056b19bcd7fee56048e004e44984e2f411788efdc837a0d2e5abb7b555039fd243ac01f0fb2ed1dec568280ce678e931868d23eb095fde9d3779191b8c0299d6e07bbb283e6633451e535c45513b2d33c99ea17')
def bsgs(g, y, p):
m = isqrt(p) + 1
S = {powmod(g, j, p): j for j in range(m)}
gs = powmod(g, -m, p)
for i in range(m):
if y in S:
return i * m + S[y]
y = y * gs % p
x = bsgs(g, y, p)
print(x)
根据题目提示,可以根据r的取值先计算求出k的值(r≡(g<sup>k</sup> mod p) mod q);因为2^16穷举一下很轻松
def fastExpMod(b, e, m): # 快速幂取模函数；b为底数，e为指数，m为模数
result = 1
while e != 0:
if (e & 1) == 1:
result = (result * b) % m
e >>= 1
b = (b * b) % m
return result # 返回取模结果
p = 0x800000000000000089e1855218a0e7dac38136ffafa72eda7859f2171e25e65eac698c1702578b07dc2a1076da241c76c62d374d8389ea5aeffd3226a0530cc565f3bf6b50929139ebeac04f48c3c84afb796d61e5a4f9a8fda812ab59494232c7d2b4deb50aa18ee9e132bfa85ac4374d7f9091abc3d015efc871a584471bb1
q = 0xf4f47f05794b256174bba6e9b396a7707e563c5b
g = 0x5958c9d3898b224b12672c0b98e06c60df923cb8bc999d119458fef538b8fa4046c8db53039db620c094c9fa077ef389b5322a559946a71903f990f1f7e0e025e2d7f7cf494aff1a0470f5b64c36b625a097f1651fe775323556fe00b3608c887892878480e99041be601a62166ca6894bdd41a7054ec89f756ba9fc95302291
y = 0x84ad4719d044495496a3201c8ff484feb45b962e7302e56a392aee4abab3e4bdebf2955b4736012f21a08084056b19bcd7fee56048e004e44984e2f411788efdc837a0d2e5abb7b555039fd243ac01f0fb2ed1dec568280ce678e931868d23eb095fde9d3779191b8c0299d6e07bbb283e6633451e535c45513b2d33c99ea17
r = 548099063082341131477253921760299949438196259240
#先恢复k的值，穷举1-65536
for k in range(2**16):
temp=fastExpMod(g,k,p)
temp %=q
if temp == r:
break
else:
pass
print("k=",k)
#k= 16575
其次,可以根据s的取值计算x:
从s≡[k<sup>-1</sup>(H(M)+xr)] mod p,可以继续推出x≡r<sup>-1</sup> * [ks-H(M)] mod q
这一步将要计算r<sup>-1</sup>的取值,用到一个自定义的求模逆函数:findModReverse,函数原理是基于扩展欧几里得算法求模逆
def gcd(a, b): # 求最大公约数函数
while a != 0:
a, b = b % a, a
return b
def findModReverse(a, m): # 这个扩展欧几里得算法求模逆
if gcd(a, m) != 1:
return None
u1, u2, u3 = 1, 0, a
v1, v2, v3 = 0, 1, m
while v3 != 0:
q = u3 // v3
v1, v2, v3, u1, u2, u3 = (u1-q*v1), (u2-q*v2), (u3-q*v3), v1, v2, v3
return u1 % m
r = 548099063082341131477253921760299949438196259240
q = 0xf4f47f05794b256174bba6e9b396a7707e563c5b
r_rev = findModReverse(r, q)
print("r^-1=", r_rev)
#r^-1= 519334352112663596410160066327650448249099314077
最后就可以恢复x并且验证签名
完整代码:
import hashlib
p = 0x800000000000000089e1855218a0e7dac38136ffafa72eda7859f2171e25e65eac698c1702578b07dc2a1076da241c76c62d374d8389ea5aeffd3226a0530cc565f3bf6b50929139ebeac04f48c3c84afb796d61e5a4f9a8fda812ab59494232c7d2b4deb50aa18ee9e132bfa85ac4374d7f9091abc3d015efc871a584471bb1
q = 0xf4f47f05794b256174bba6e9b396a7707e563c5b
g = 0x5958c9d3898b224b12672c0b98e06c60df923cb8bc999d119458fef538b8fa4046c8db53039db620c094c9fa077ef389b5322a559946a71903f990f1f7e0e025e2d7f7cf494aff1a0470f5b64c36b625a097f1651fe775323556fe00b3608c887892878480e99041be601a62166ca6894bdd41a7054ec89f756ba9fc95302291
y = 0x84ad4719d044495496a3201c8ff484feb45b962e7302e56a392aee4abab3e4bdebf2955b4736012f21a08084056b19bcd7fee56048e004e44984e2f411788efdc837a0d2e5abb7b555039fd243ac01f0fb2ed1dec568280ce678e931868d23eb095fde9d3779191b8c0299d6e07bbb283e6633451e535c45513b2d33c99ea17
hash_x = 0x0954edd5e0afe5542a4adf012611a91912a3ec16
Hash_M = 0xd2d0714f014a9784047eaeccf956520045c45265
r = 548099063082341131477253921760299949438196259240
s = 857042759984254168557880549501802188789837994940
def fastExpMod(b, e, m): # 快速幂取模函数；b为底数，e为指数，m为模数
result = 1
while e != 0:
if (e & 1) == 1:
result = (result * b) % m
e >>= 1
# b, b^2, b^4, b^8, ... , b^(2^n)
b = (b * b) % m
return result
def gcd(a, b): # 求最大公约数函数
while a != 0:
a, b = b % a, a
return b
def findModReverse(a, m): # 这个扩展欧几里得算法求模逆
if gcd(a, m) != 1:
return None
u1, u2, u3 = 1, 0, a
v1, v2, v3 = 0, 1, m
while v3 != 0:
q = u3 // v3
v1, v2, v3, u1, u2, u3 = (u1 - q * v1), (u2 - q * v2), (u3 - q * v3), v1, v2, v3
return u1 % m
if __name__ == '__main__':
# 先恢复k的值，穷举1-65536
for k in range(2 ** 16):
temp = fastExpMod(g, k, p)
temp %= q
if temp == r:
break
print("k=", k)
r_rev = findModReverse(r, q)
print("r^-1=", r_rev)
x = (k * s - Hash_M) % q
x = x * r_rev % q
print("x=", x)
hex_x = hex(x)[2:]
print("hex_x=", hex_x)
hex_x_bytes = hex_x.encode('utf-8')
Hash_x = hashlib.sha1(hex_x_bytes).hexdigest()
print("Sha1(x)=", Hash_x)
if hash_x == int(Hash_x, 16):
print("哈希匹配，求解私钥x正确！")
'''
k= 16575
r^-1= 519334352112663596410160066327650448249099314077
x= 125489817134406768603130881762531825565433175625
hex_x= 15fb2873d16b3e129ff76d0918fd7ada54659e49
Sha1(x)= 0954edd5e0afe5542a4adf012611a91912a3ec16
哈希匹配，求解私钥x正确！
'''
浙公网安备 33010602011771号