Twisted Edwards曲线

题目:

#sagemath
from Crypto.Util.number import *

def add(P, Q):
    (x1, y1) = P
    (x2, y2) = Q

    x3 = (x1*y2 + y1*x2) * inverse(1 + d*x1*x2*y1*y2, p) % p
    y3 = (y1*y2 - a*x1*x2) * inverse(1 - d*x1*x2*y1*y2, p) % p
    return (x3, y3)

def mul(x, P):
    Q = (0, 1)
    while x > 0:
        if x % 2 == 1:
            Q = add(Q, P)
        P = add(P, P)
        x = x >> 1
    return Q

p = 64141017538026690847507665744072764126523219720088055136531450296140542176327
a = 362
d = 7
e=0x10001

gx=bytes_to_long(b'D0g3xGC{*****************}')

PR.<y>=PolynomialRing(Zmod(p))
f=(d*gx^2-1)*y^2+(1-a*gx^2)
gy=int(f.roots()[0][0])

assert (a*gx^2+gy^2)%p==(1+d*gx^2*gy^2)%p

G=(gx,gy)

eG = mul(e, G)
print(eG)

#eG = (34120664973166619886120801966861368419497948422807175421202190709822232354059, 11301243831592615312624457443883283529467532390028216735072818875052648928463)

解题思路:

分析曲线

• 我们首先分析一下这是个什么曲线

  `assert (a*gx^2+gy^2)%p==(1+d*gx^2*gy^2)%p`
  

• 这是扭曲爱德华(Twisted Edwards)曲线,其一般形式为

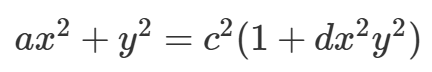
• 分析曲线结构

  

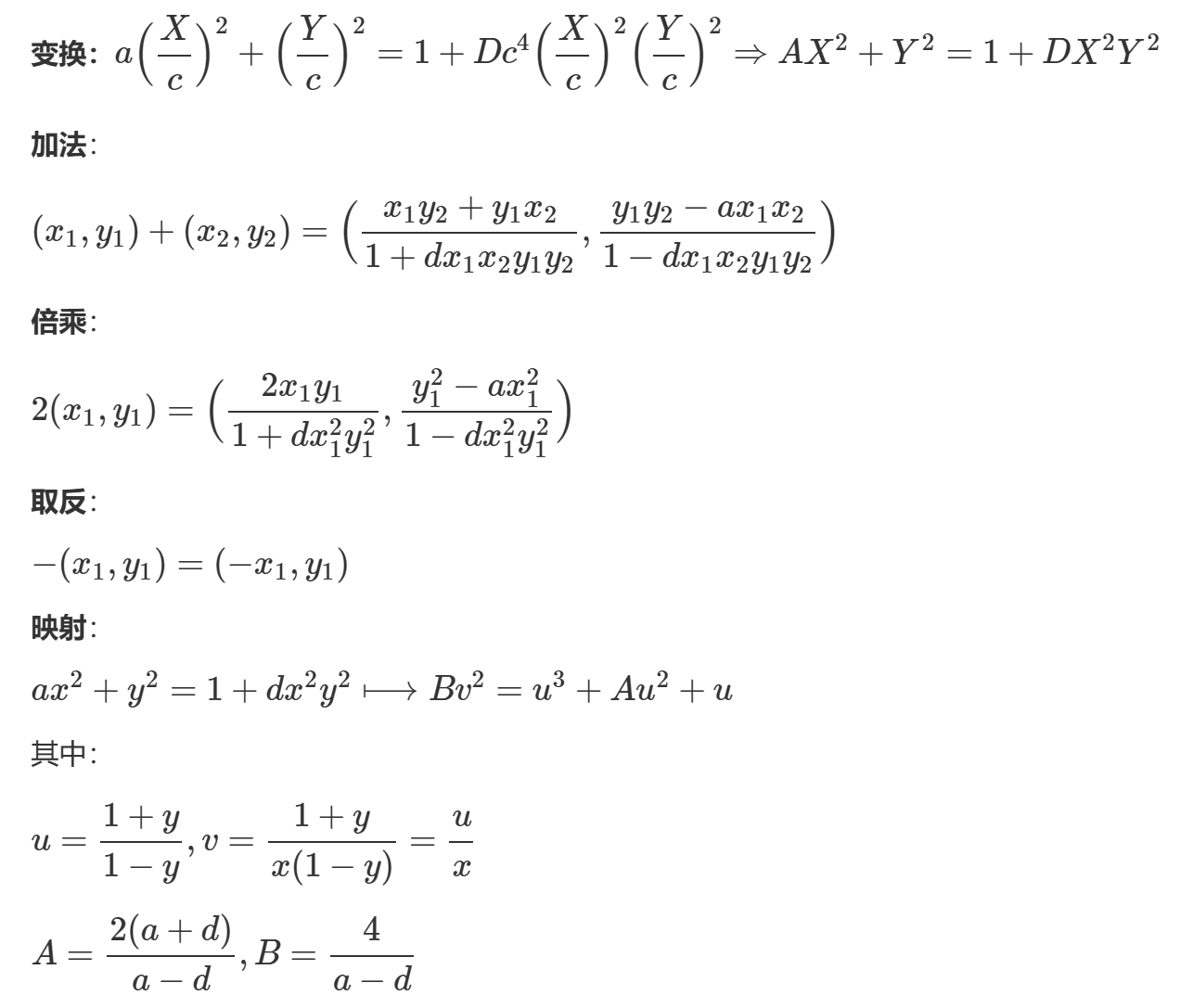
分析代码

• **p**:模数,表示椭圆曲线定义在有限域Fp上

**a**和**d**:椭圆曲线的参数,用于定义曲线的方程:ax<sup>2</sup>+y<sup>2</sup>≡1+dx<sup>2</sup>y<sup>2 </sup>(mod p)

**e**:公钥指数

**gx**:基点<font style="color:rgb(6, 6, 7);">G</font>的<font style="color:rgb(6, 6, 7);">x</font>坐标,通过<font style="color:rgb(6, 6, 7);">bytes_to_long</font>将一个字节序列转换为整数

• f = (d * gx^2 - 1) * y^2 + (1 - a * gx^2)

**f**:构造一个关于<font style="color:rgb(6, 6, 7);">y</font>的多项式,用于求解<font style="color:rgb(6, 6, 7);">y</font>坐标

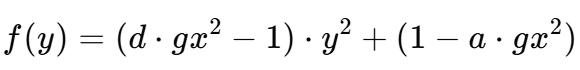
• gy = int(f.roots()[0][0])

**gy**:通过求解多项式<font style="color:rgb(6, 6, 7);">f(y)</font>的根,得到<font style="color:rgb(6, 6, 7);">y</font>坐标;<font style="color:rgb(6, 6, 7);">roots()</font>方法返回多项式的根,取第一个根作为<font style="color:rgb(6, 6, 7);">gy</font>

**G**:基点

**eG**:通过标量乘法eG计算加密后的点

解密思路

• 在代码中,加密过程是通过将基点<font style="color:rgb(6, 6, 7);">G</font>乘以公钥<font style="color:rgb(6, 6, 7);">e</font>来完成的,即<font style="color:rgb(6, 6, 7);">eG</font>
• 解密过程需要找到私钥<font style="color:rgb(6, 6, 7);">d</font>,使得<font style="color:rgb(6, 6, 7);">d × e ≡ 1 (mod n)</font>,其中<font style="color:rgb(6, 6, 7);">n</font>是椭圆曲线的阶
• 那么如何求阶呢,似乎没有办法直接求这种圆锥曲线的阶,不过我们可以将Edcurve通过换元映射,变换为常见的椭圆曲线的形式

换元映射

• 第一步:转化为蒙哥马利曲线方程(Montgomery)

  ![](https://cdn.nlark.com/yuque/0/2025/png/49294098/1739691305781-2dd4d4ee-aee7-4e26-87cb-59c99d81af3d.png)
  

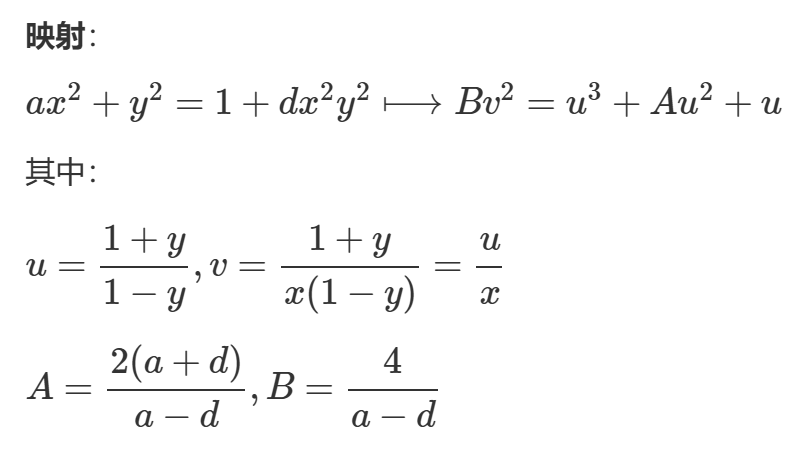• 第二步:转化为椭圆曲线方程(Weierstrass)

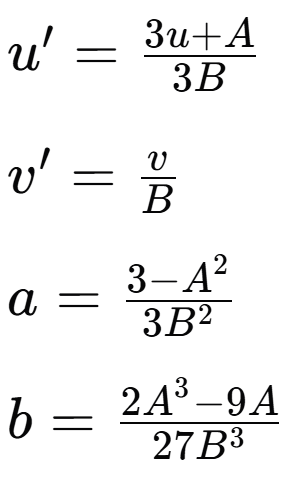
• 此时蒙哥马利曲线就变成了椭圆曲线方程形式

   ![](https://cdn.nlark.com/yuque/0/2025/png/49294098/1739692113095-16b94fe0-11f5-41d7-be17-aa894404ecc5.png)
  

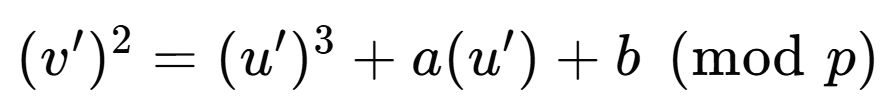• 然后求该曲线的阶,从而求解出远原点G,并且重新逆变换回Edcurve,得到的横坐标即为flag

代码分步实现

• 映射到椭圆曲线

F = GF(p)
dd = F(d*c^4)
A = F(2) * F(a+dd) / F(a-dd)
B = F(4) / F(a-dd)
a = F(3-A^2) / F(3*B^2)
b = F(2*A^3-9*A) / F(27*B^3)

• 映射函数

def edwards_to_ECC(x,y):
    x1 = F(x) / F(c)
    y1 = F(y) / F(c)
    x2 = F(1+y1) / F(1-y1)
    y2 = F(x2) / F(x1)
    x3 = (F(3*x2) + F(A)) / F(3*B)
    y3 = F(y2) / F(B)
    return (x3,y3)

def ECC_to_edwards(x,y):
    x2 = (F(x) * F(3*B) - F(A)) / F(3)
    y2 = F(y) * F(B)
    x1 = F(x2) / F(y2)
    y1 = F(1) - (F(2) / F(x2+1))
    x_ = F(x1) * F(c)
    y_ = F(y1) * F(c)
    return (x_,y_)

edwards_to_ECC(x, y):将Twisted Edwards曲线上的点映射到椭圆曲线上

ECC_to_edwards(x, y):将椭圆曲线上的点映射回Twisted Edwards曲线

• 解密过程

E = EllipticCurve(GF(p), [a, b])
order = E.order()
eG = E(edwards_to_ECC(eG[0],eG[1]))
t = inverse(e,order)
G = t*eG
G = ECC_to_edwards(G[0],G[1])
print(bytes.fromhex(hex(G[0])[2:]))

创建椭圆曲线E

计算椭圆曲线的阶order

将加密后的点eG映射到椭圆曲线上

计算私钥t,即公钥e的模逆元

使用私钥t解密,得到原始点G

将解密后的点G映射回Twisted Edwards曲线

输出解密结果,即原始消息的哈希值

解答:

p = 64141017538026690847507665744072764126523219720088055136531450296140542176327
a = 362
d = 7
c = 1
e = 0x10001
eG = (34120664973166619886120801966861368419497948422807175421202190709822232354059, 11301243831592615312624457443883283529467532390028216735072818875052648928463)

#part2 map to ECC
F = GF(p)
dd = F(d*c^4)
A = F(2) * F(a+dd) / F(a-dd)
B = F(4) / F(a-dd)
a = F(3-A^2) / F(3*B^2)
b = F(2*A^3-9*A) / F(27*B^3)

def edwards_to_ECC(x,y):
    x1 = F(x) / F(c)
    y1 = F(y) / F(c)
    #now curve is a*x^2+y^2 = 1+dd*x^2*y^2

    x2 = F(1+y1) / F(1-y1)
    y2 = F(x2) / F(x1)
    #now curve is By^2 = x^3 + Ax^2 + x

    x3 = (F(3*x2) + F(A)) / F(3*B)
    y3 = F(y2) / F(B)
    #now curve is y^2 = x^3 + ax + b

    return (x3,y3)
 
def ECC_to_edwards(x,y):
    x2 = (F(x) * F(3*B) - F(A)) / F(3)
    y2 = F(y) * F(B)
    #now curve is By^2 = x^3 + Ax^2 + x

    x1 = F(x2) / F(y2)
    y1 = F(1) - (F(2) / F(x2+1))
    #now curve is a*x^2+y^2 = 1+dd*x^2*y^2

    x_ = F(x1) * F(c)
    y_ = F(y1) * F(c)
    #now curve is a*x^2+y^2 = c^2(1+d*x^2*y^2)
    
    return (x_,y_)
 
E = EllipticCurve(GF(p), [a, b])
order = E.order()
eG = E(edwards_to_ECC(eG[0],eG[1]))
t = inverse_mod(e,order)
G = t*eG
G = ECC_to_edwards(G[0],G[1])
print(bytes.fromhex(hex(G[0])[2:]))
#D0g3xGC{SOlvE_The_Edcurv3}