Elliptic(椭圆)曲线

题目:

from Crypto.Util.number import getPrime
from libnum import s2n
from secret import flag

p = getPrime(256)
a = getPrime(256)
b = getPrime(256)
E = EllipticCurve(GF(p),[a,b])
m = E.random_point()
G = E.random_point()
k = getPrime(256)
K = k * G
r = getPrime(256)
c1 = m + r * K
c2 = r * G
cipher_left = s2n(flag[:len(flag)//2]) * m[0]
cipher_right = s2n(flag[len(flag)//2:]) * m[1]

print(f"p = {p}")
print(f"a = {a}")
print(f"b = {b}")
print(f"k = {k}")
print(f"E = {E}")
print(f"c1 = {c1}")
print(f"c2 = {c2}")
print(f"cipher_left = {cipher_left}")
print(f"cipher_right = {cipher_right}")
'''
p = 74997021559434065975272431626618720725838473091721936616560359000648651891507
a = 61739043730332859978236469007948666997510544212362386629062032094925353519657
b = 87821782818477817609882526316479721490919815013668096771992360002467657827319
k = 93653874272176107584459982058527081604083871182797816204772644509623271061231
E = Elliptic Curve defined by y^2 = x^3 + 61739043730332859978236469007948666997510544212362386629062032094925353519657*x + 12824761259043751634610094689861000765081341921946160155432001001819005935812 over Finite Field of size 74997021559434065975272431626618720725838473091721936616560359000648651891507
c1 = (14455613666211899576018835165132438102011988264607146511938249744871964946084 : 25506582570581289714612640493258299813803157561796247330693768146763035791942 : 1)
c2 = (37554871162619456709183509122673929636457622251880199235054734523782483869931 : 71392055540616736539267960989304287083629288530398474590782366384873814477806 : 1)
cipher_left = 68208062402162616009217039034331142786282678107650228761709584478779998734710
cipher_right = 27453988545002384546706933590432585006240439443312571008791835203660152890619
'''

解题思路:

• 我们首先分析这个曲线方程的形式为一个椭圆曲线方程

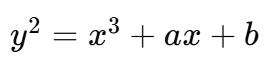
• 分析一下结构

  ![](https://cdn.nlark.com/yuque/0/2025/png/49294098/1739610463741-5a93cb22-635c-473a-8ca3-59f6af11be45.png)
  

• p是一个大素数,定义了椭圆曲线的有限域<font style="color:rgb(6, 6, 7);">Fp</font>

• a和b是椭圆曲线的参数

• EllipticCurve(GF(p), [a, b])定义了椭圆曲线<font style="color:rgb(6, 6, 7);">E</font>

• <font style="color:rgb(6, 6, 7);">m</font>和<font style="color:rgb(6, 6, 7);">G</font>是椭圆曲线<font style="color:rgb(6, 6, 7);">E</font>上的随机点

• k是一个私钥

• K = k * G是椭圆曲线上的标量乘法,表示将点G乘以标量k,得到点K

• r是一个随机生成的256位素数

• c1 = m + r * K是椭圆曲线上的点加法,将点m和点r * K相加

• c2 = r * G是椭圆曲线上的标量乘法

• m[0]和m[1]分别是椭圆曲线点m的<font style="color:rgb(6, 6, 7);">x</font>坐标和<font style="color:rgb(6, 6, 7);">y</font>坐标

• c_left和c_right是加密后的消息片段,通过将消息片段与椭圆曲线点的坐标相乘得到

• 涉及加密解密的所有参数都已经给出,flag只和m有关,而m的解密只涉及ECC的基本解密流程

• 

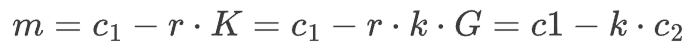
解答:

p = 74997021559434065975272431626618720725838473091721936616560359000648651891507
a = 61739043730332859978236469007948666997510544212362386629062032094925353519657
b = 12824761259043751634610094689861000765081341921946160155432001001819005935812
k = 93653874272176107584459982058527081604083871182797816204772644509623271061231
E = EllipticCurve(GF(p), [a, b])
c1 = E([14455613666211899576018835165132438102011988264607146511938249744871964946084,
        25506582570581289714612640493258299813803157561796247330693768146763035791942])
c2 = E([37554871162619456709183509122673929636457622251880199235054734523782483869931,
        71392055540616736539267960989304287083629288530398474590782366384873814477806])
cipher_left = 68208062402162616009217039034331142786282678107650228761709584478779998734710
cipher_right = 27453988545002384546706933590432585006240439443312571008791835203660152890619
m = c1 - k * c2
left = cipher_left // m[0]
right = cipher_right // m[1]
print(hex(int(left)) + hex(int(right)))
print(bytes.fromhex(hex(left)[2:])+bytes.fromhex(hex(right)[2:]))
#0x6867616d657b456363240x697321734f40486152647d
#hgame{Ecc$is!sO@HaRd}

题目:

from Crypto.Util.number import * # type: ignore
from secret import flag

p = 64408890408990977312449920805352688472706861581336743385477748208693864804529
a = 111430905433526442875199303277188510507615671079377406541731212384727808735043
b = 89198454229925288228295769729512965517404638795380570071386449796440992672131
E = EllipticCurve(GF(p),[a,b])
m = E.random_point()
G = E.random_point()
k = 86388708736702446338970388622357740462258632504448854088010402300997950626097
K = k * G
r = getPrime(256)
c1 = m + r * K
c2 = r * G
c_left =bytes_to_long(flag[:len(flag)//2]) * m[0]
c_right = bytes_to_long(flag[len(flag)//2:]) * m[1]

print(f"c1 = {c1}")
print(f"c2 = {c2}")
print(f"cipher_left = {c_left}")
print(f"cipher_right = {c_right}")

'''
c1 = (10968743933204598092696133780775439201414778610710138014434989682840359444219 : 50103014985350991132553587845849427708725164924911977563743169106436852927878 : 1)
c2 = (16867464324078683910705186791465451317548022113044260821414766837123655851895 : 35017929439600128416871870160299373917483006878637442291141472473285240957511 : 1)
c_left = 15994601655318787407246474983001154806876869424718464381078733967623659362582
c_right = 3289163848384516328785319206783144958342012136997423465408554351179699716569
'''

解答:

p = 64408890408990977312449920805352688472706861581336743385477748208693864804529
a = 111430905433526442875199303277188510507615671079377406541731212384727808735043
b = 89198454229925288228295769729512965517404638795380570071386449796440992672131
k = 86388708736702446338970388622357740462258632504448854088010402300997950626097
E = EllipticCurve(GF(p), [a, b])
c1 = E([10968743933204598092696133780775439201414778610710138014434989682840359444219,50103014985350991132553587845849427708725164924911977563743169106436852927878])
c2 = E([16867464324078683910705186791465451317548022113044260821414766837123655851895,35017929439600128416871870160299373917483006878637442291141472473285240957511])
cipher_left = 15994601655318787407246474983001154806876869424718464381078733967623659362582
cipher_right = 3289163848384516328785319206783144958342012136997423465408554351179699716569
m = c1 - k * c2
left = cipher_left // m[0]
right = cipher_right // m[1]
print(hex(int(left)) + hex(int(right)))
print(bytes.fromhex(hex(left)[2:])+bytes.fromhex(hex(right)[2:]))
#0x666c61677b546869735f69735f74680x655f6c6173745f63727970746f5f7d
#flag{This_is_the_last_crypto_}