(p^q)>>nbits
题目1:
from Crypto.Util.number import *
from secret import flag
nbits=512
p=getPrime(nbits)
q=getPrime(nbits)
leakBits = 262
leak = (p ^ q) >> (nbits - leakBits)
n=p*q
e=65537
m = bytes_to_long(flag)
c = pow(m,e,n)
print(p)
print(q)
print("n=%d" %n)
print("c=%d" %c)
print("leak=%d" %leak)
# n=73822410148110759760164946405270228269255384237831275745269402590230495569279769799226813942899942423718229747478982630879557319063920515141217164980012063064986634632452289290326704640527699568662492105204165609614169349755365956569362139057327962393611139347462018186440108621311077722819578905265976612923
# c=71808322808599218331233291542779486534747913572475630198802984648982830332628443972652322590637382696027943799004331488098592525306523343649935216419522329722152742610560398216737030893090641493326477786720839849938277402743820773957184083430369443325368720115515840174745825798187125454448297155036065857691
# leak=2223117424030234543005449667053988296724455736030907136592525175314696509716321
解题思路:
nbits = 512
p = getPrime(nbits)
q = getPrime(nbits)
leakBits = 262
leak = (p ^ q) >> (nbits - leakBits)
搜索方式:
- 从高位搜索
p的高位乘q的高位的前半部分等于n的高位
剪枝条件:
- 低位全补
0,相乘结果< n - 低位全补
1,相乘结果> n
p = '1'
q = '1'
P = [p]
Q = [q]
for i in range(261):
PP = []
QQ = []
for a in '01':
for b in '01':
for pnew, qnew in zip(P, Q):
pnew = pnew + a
qnew = qnew + b
tmp = int(pnew, 2) * int(qnew, 2)
if int(pnew, 2) ^ int(qnew, 2) == int(leak_bin[:2 + i], 2) and tmp >> (tmp.bit_length() - i // 2) == n >> (n.bit_length() - i // 2) and (int(pnew.ljust(512, '0'), 2) * int(qnew.ljust(512, '0'), 2) < n) and (int(pnew.ljust(512, '1'), 2) * int(qnew.ljust(512, '1'), 2) > n):
PP.append(pnew)
QQ.append(qnew)
print(len(P))
P = PP.copy()
Q = QQ.copy()
print(P)
上述剪枝只能求出高262位了,有多种组合,但仍缺少低250位,因此需要用到coppersmith来求解
在具体应用情景中应当适当调整beta和epsilon
from tqdm import *
R.<x> = Zmod(n)[]
for pbar in tqdm(P[::-1]):
for i in range(32):
tmp = int(pbar,2)<<5
tmp+=i
f = tmp*2**245 + x
xx = f.monic().small_roots(X=2^245,beta=0.47,epsilon=0.02)
if xx:
p = f(xx[0])
print(p)
以上只是通俗的想法
具体来说:
题目给了一个泄漏了高262位的leak,满足:leak=p^q
那么运用深搜,可以找到多组满足条件的p,q高位
那么接下来的自然想法,就是对找到的这些可能的p,q高位依次进行copper恢复低位,但是有一点小问题:
- 未知的低位有
250比特,对于copper来说比较紧
所以我们要想办法提高可解根的上界,而我们知道,copper的可解根上界如下:
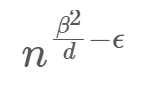
其中,d是构造的待求解多项式的度,这里也就是1;beta是指多项式建立在有限域Z(p)上,p是n的因子且满足b>n^beta;epsilon就是small_roots的一个参数
那么可以运用下面三个思路更好的利用copper:
- 每一组比较
p,q高位的大小,取较大的那一个值来恢复低位,这样可以将beta取为0.5,提高能求解的理论上界 epsilon取0.01,这样会变慢,但同样可以提高能求解的理论上界- 由于
p为素数,将待求的p最低位赋为1,可以缩小根的上界(同理,可以爆破几位进一步缩小上界,但这里不需要了)
然后就可以恢复p,进而求解明文
解答:
完整代码:
import sys
sys.setrecursionlimit(1500)
nbits=512
leakBits = 262
leakbits = nbits - leakBits
e = 65537
n=73822410148110759760164946405270228269255384237831275745269402590230495569279769799226813942899942423718229747478982630879557319063920515141217164980012063064986634632452289290326704640527699568662492105204165609614169349755365956569362139057327962393611139347462018186440108621311077722819578905265976612923
c=71808322808599218331233291542779486534747913572475630198802984648982830332628443972652322590637382696027943799004331488098592525306523343649935216419522329722152742610560398216737030893090641493326477786720839849938277402743820773957184083430369443325368720115515840174745825798187125454448297155036065857691
leak=2223117424030234543005449667053988296724455736030907136592525175314696509716321
leak = leak << leakbits
a1 = "0" + str(bin(leak)[2:])
def find(p,q):
l = len(p)
tmp0 = p + (512-l)*"0"
tmp1 = p + (512-l)*"1"
tmq0 = q + (512-l)*"0"
tmq1 = q + (512-l)*"1"
if(int(tmp0,2) < int(tmq0,2)):
return
if(int(tmp0,2)*int(tmq0,2) > n):
return
elif(int(tmp1,2)*int(tmq1,2) < n):
return
if(l == 512 - leakbits):
pp = int(tmp0,2)
PR.<x> = PolynomialRing(Zmod(n))
f = pp + x*2 + 1
f = f.monic()
res = f.small_roots(X=2^leakbits-1, beta=0.5, epsilon=0.01)
if(res):
try:
plow = int(res[0])
p = pp + plow * 2 + 1
q = n // p
d = inverse_mod(e,(p-1)*(q-1))
print(bytes.fromhex(hex(pow(c,d,n))[2:]))
except:
pass
else:
if(a1[l] == "1"):
find(p+"1",q+"0")
find(p+"0",q+"1")
else:
find(p+"0",q+"0")
find(p+"1",q+"1")
tempp = ""
tempq = ""
find(tempp,tempq)
'''
b'$\x0c&p\xaf\xd8M\xb7\xff\x06\xf9\xe1\xf1\xb6<"\xb8\xb3\x95\x11\x18\x96\xe0\\Ff\xab\x15\xdd\x92\xb2\xcfu\\~\x1e\xf3\x9bEu\xa7vd\xa2\xd7\xfd\xf1\xb5h\xf6\x18\xe6\xaf\xfd\xdf\xaf\x0f\x0b\xa0g\xb7\xc5\x8d"\xb8v\xee\x18\x08\xfd\x84Y\xd5\x80\x8c\x0c\xbf3X\xd2?\xa1\xf8\xae\xc5\xb7\x1c1\x83\\\xf3e\x12\xd8\x95\xc2W-k|\xa2 w`9\xbaG\x1f\xb5<\x1a=\xa6L\x07\xac\x87vID"\xa5\x9b\xc0\xd8\xe2P\x8e'
b'flag{6eb67115-38b1-4e75-b3fc-de3a9697e565}'
'''
题目2:
from Crypto.Util.number import *
import uuid
flag = "flag{" + str(uuid.uuid4()) + "}"
print(flag)
m = bytes_to_long(flag.encode())
p = getPrime(1024)
q = getPrime(1024)
e = 65537
gift = (p ^ q) >> 400
n = p * q
print(gift)
print(n)
c = pow(m, e, n)
print(c)
'''
n = 18706855965472342624057939763424482872214329403736588022670810823830284968210885370388661001166733799554843541458754316300002655734547865499832294251476719959685339472505232553318035696334043294583493018799085665100973395464171935497665253854897019585848130524402110067723380001729487763295805724049305195847415832438554371670757918022485495294646131894414072289025724167436635324722072486662116496042680216887523471775800611333173420803326625619428964822316053642973227668518358385684985208861639528026293678346064873875113765964212781464014313025439732581964381711834800618756897046018036356342152039250047100962433
gift = 31804842194481800642289237939366333950938402156162359676516215207202180995245509557106597907613130513998342782732102690555165790483400730844362691314157824965589453046147635163730354622709
c = 12794209312573575749100915624211637292155365912707165305418491442314056699524137698990172074503800252273733761237854112762666157382998208601175150915064715204047907876367016385260965822781044525231089378759441364134208537808855535974753177409801491254478458330987262277165144909736422815482607722757203398963207791454184689820020716763711923377454162849497041563361402795290662590809159204490290459091960419194993377210983171994701178608788724920126553968410593513625304851116511549261271900279711693939689339127996950002029576453531700368097632402268119653383995840345178053336060126043684143615733387687606189824034
'''
解题思路:
这个题目和上面(p^(q>>nbits))不一样就是p^q的值进行了移位操作,那么我们就不知道低位的值,也就不能从低位爆破了
那么能不能从高位爆破,问题就在于如何提取高位,我们在上面通过取模得到低位,那么高位只能通过移位获取
这里有个问题就是我们没办法爆破得到所有的位数,因为移位后的数据被抹掉了
但是我们可以爆破到已知的位数,然后利用coppersmith定理求取未知的部分
总结就是第一个情况需要从低位开始爆破,第二个情况就是从高位开始
下面总结两个脚本方法,原理都是从高位开始
解答:
N = 18706855965472342624057939763424482872214329403736588022670810823830284968210885370388661001166733799554843541458754316300002655734547865499832294251476719959685339472505232553318035696334043294583493018799085665100973395464171935497665253854897019585848130524402110067723380001729487763295805724049305195847415832438554371670757918022485495294646131894414072289025724167436635324722072486662116496042680216887523471775800611333173420803326625619428964822316053642973227668518358385684985208861639528026293678346064873875113765964212781464014313025439732581964381711834800618756897046018036356342152039250047100962433
gift = 31804842194481800642289237939366333950938402156162359676516215207202180995245509557106597907613130513998342782732102690555165790483400730844362691314157824965589453046147635163730354622709
gift <<=400
PR.<x> = PolynomialRing(Zmod(N))
ok = False
def pq_xor(tp,tq,idx):
global ok
if ok:
return
if tp*tq>N:
return
if (tp+(2<<idx))*(tq+(2<<idx))<N:
return
if idx<=400:
try:
f = tp + x
rr = f.monic().small_roots(X=2^400, beta=0.4)
if rr != []:
print(rr)
print(tp)
print('p = ',f(rr[0]))
ok = True
return
except:
pass
return
idx -=1
b = (gift >>idx)&1
one = 1<<idx
if b==0:
pq_xor(tp,tq,idx)
pq_xor(tp+one,tq+one,idx)
else: #1
pq_xor(tp+one,tq,idx)
pq_xor(tp,tq+one,idx)
tp = 1<<1023
tq = 1<<1023
pq_xor(tp,tq,1023)
'''
[1642720344911246936419419209239848298354041818594298333321528470715860323831664108676250409253088326371239980812896996061]
156312751820343202096817187657750965338488513824160102689481418250930593561890157208297426377931154984541743793038361097646017514839938385390736541319606636813885703108633813056309263784286100988106344901864347326469047102283922248479393744028973716179243093028251277526401051569780449138435902217460543127552
p = 156312751820343202096817187657750965338488513824160102689481418250930593561890157208297426377931154984541743793038361097646017514839938385390736541319606636813885703108633813056309263784287743708451256148800766745678286950582276290297988042362295244649958953352082941635077301979033537464807142198273440123613
'''
from Crypto.Util.number import *
import gmpy2
p = 156312751820343202096817187657750965338488513824160102689481418250930593561890157208297426377931154984541743793038361097646017514839938385390736541319606636813885703108633813056309263784287743708451256148800766745678286950582276290297988042362295244649958953352082941635077301979033537464807142198273440123613
gift = 31804842194481800642289237939366333950938402156162359676516215207202180995245509557106597907613130513998342782732102690555165790483400730844362691314157824965589453046147635163730354622709
n = 18706855965472342624057939763424482872214329403736588022670810823830284968210885370388661001166733799554843541458754316300002655734547865499832294251476719959685339472505232553318035696334043294583493018799085665100973395464171935497665253854897019585848130524402110067723380001729487763295805724049305195847415832438554371670757918022485495294646131894414072289025724167436635324722072486662116496042680216887523471775800611333173420803326625619428964822316053642973227668518358385684985208861639528026293678346064873875113765964212781464014313025439732581964381711834800618756897046018036356342152039250047100962433
c = 12794209312573575749100915624211637292155365912707165305418491442314056699524137698990172074503800252273733761237854112762666157382998208601175150915064715204047907876367016385260965822781044525231089378759441364134208537808855535974753177409801491254478458330987262277165144909736422815482607722757203398963207791454184689820020716763711923377454162849497041563361402795290662590809159204490290459091960419194993377210983171994701178608788724920126553968410593513625304851116511549261271900279711693939689339127996950002029576453531700368097632402268119653383995840345178053336060126043684143615733387687606189824034
e = 65537
q = n // p
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))
#flag{3b3669f5-387d-4cd1-8924-d12f290ac145}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号