模多项式求根-Coppersmith方法

题目:

from Crypto.Util.number import *
flag = b'NSSCTF{******}'

m = bytes_to_long(flag)

a = getPrime(512)
b = getPrime(512)
c = getPrime(512)
d = getPrime(512)
x = getPrime(128)

p = getPrime(1024)

y = a*x**3 + b*x**2 + c*x + d
y = y%p

print(f'p = {p}')
print(f'a = {a}')
print(f'b = {b}')
print(f'c = {c}')
print(f'd = {d}')
print(f'y = {y}')
print(f'h = {x*m}')

'''
p = 133497915779382863191750985139274661777547262395290628161924420897772911005538338729076080701700641387222690295548776566406640902391412661622674862629221960258683570655393881212072865809598640669325347893228617784548982886334708010706482958773921901369314425694414231562752232070402056445403762485870067804611
a = 9956367951694116871507184264812038680047685394446603010101493156120195118634053526664122377707243776744926630820373051608195739431033785355316509320690639
b = 10372715760267086803036635068149481902075294943354407472550232447612611381527989796797133302495652064200149218004252582942179771677307157495328484190016267
c = 6954444546090251351899752282258945069765577103755637726562318645879810909547057855773433206441550954298878711294660493586907360045986061150306446126101573
d = 12708905621484064085174866220764918657140490021181156214236692898034114314742314389460399916798129560082685314351680895409634875081403212130502800572290391
y = 89881957270704175663646084308402351944545222001266778194637035700540903495792268004845278611707036762628657152963392762363015748904045511650663013086598899685992255568758440781657480520250399778976982455784259655683731183717562593121780657623767804362641533930566522430
h = 584447473604416360596641349947186936435346265446590336271443321812736224750414727189483734666053582372219773206703655293254283559436185831581631
'''

解题思路:

对于一个模意义下的多项式函数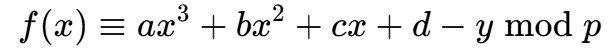求解其根或者说零点

…………???

知识拓展:

1.环

群环域,都是抽象代数中的一些概念,在我们之前的内容都是对具体的值做运算,我们的操作对象是元素,在抽象代数中,把运算符和运算规则也作为了一种操作对象进行操作,通过包含不同性质和运算符的集合创造了群环域这些概念

对于环来说,它包含两个二元运算(我们一般称为加法和乘法,注意我们只是这么叫,具体运算和环定义有关),并且满足一些例如分配律,结合律的运算规则.而多项式环则是至其中的元素对象为一个多项式,对于抽代来说,一切都是基于初始的定义进行衍生的,我们不能再以以往的经验来进行操作,例如a+b=b+a,a⋅b=a+⋯+a等等这些法则在抽代中是需要证明或被定义的

2.伽罗瓦域(Galois Field)也称有限域

有限域是域中的一种,域在抽代中和环的区别就是有无乘法逆元,存在乘法逆元的环就是域.而有限域则是一个模域,即域是在模p以下成立的

解答:

from gmpy2 import *

p = 133497915779382863191750985139274661777547262395290628161924420897772911005538338729076080701700641387222690295548776566406640902391412661622674862629221960258683570655393881212072865809598640669325347893228617784548982886334708010706482958773921901369314425694414231562752232070402056445403762485870067804611
a = 9956367951694116871507184264812038680047685394446603010101493156120195118634053526664122377707243776744926630820373051608195739431033785355316509320690639
b = 10372715760267086803036635068149481902075294943354407472550232447612611381527989796797133302495652064200149218004252582942179771677307157495328484190016267
c = 6954444546090251351899752282258945069765577103755637726562318645879810909547057855773433206441550954298878711294660493586907360045986061150306446126101573
d = 12708905621484064085174866220764918657140490021181156214236692898034114314742314389460399916798129560082685314351680895409634875081403212130502800572290391
y = 89881957270704175663646084308402351944545222001266778194637035700540903495792268004845278611707036762628657152963392762363015748904045511650663013086598899685992255568758440781657480520250399778976982455784259655683731183717562593121780657623767804362641533930566522430
h = 584447473604416360596641349947186936435346265446590336271443321812736224750414727189483734666053582372219773206703655293254283559436185831581631

PR.<x> = PolynomialRing(GF(p))
f = a*x^3 + b*x^2 + c*x + d - y
f = f.monic()
res = f.small_roots()
m = h // int(res[0])
print(bytes.fromhex(hex(m)[2:]))
#NSSCTF{fdf4236b-50a9-4d4b-96fb-fe9ba9d7dff7}

PR. = PolynomialRing(GF(p))是Sage的独有语法,其变量名为PR

代表代表多项式环中的变量标识符

后面的PolynomialRing即字面意思多项式环

GF(p)代表一个模数为p的有限域