题目:
from Crypto.Util.number import *
import os
from gmpy2 import *
def getMyPrime1(nbits):
while True:
n = 2*1009*7*getPrime(nbits//2)*getPrime(nbits//2)
if is_prime(n+1):
return n+1
def getMyPrime2(nbits):
while True:
n = 2*1009*getPrime(nbits//2)*getPrime(nbits//2)
if is_prime(n+1):
return n+1
p = getMyPrime1(700)
q = getMyPrime2(700)
n = p*q
e = 1009*7
flag = b'NSSCTF{******}' + os.urandom(100)
m = bytes_to_long(flag)
assert m.bit_length() < n.bit_length()
assert m.bit_length() > q.bit_length()
assert m.bit_length() > p.bit_length()
c = pow(m, e, n)
print(f'n = {n}')
print(f'c = {c}')
print(f'p = {p}')
print(f'q = {q}')
'''
n = 98950849420612859614279452190318782153029931966597217314273823358984928689736597943774367572478091193816498014404387458350141854427041188032441028722132300155987022405432547244436252627801235200799719531840755071562539171489733346246951714886747673950900290905148318965065773167290984966067642777528454814019184856012497536781760044965489668142694134954466581148235162435617572891367282110999553789319439912296241889469226304877
c = 22561646796929363815984273658718096881828574147472740106912668949512978818367595303883956088667384207835022579136977262135029404640598574466248596921339941958216824486529066880854722372158998556902335323841170236300423638675072077074005797219260622119718558697081430219981494670569821476853158740209737420919480047033900157150865588466910802691118334480300332681763467974691587834295938999022060676767513865584039532912503921584
p = 33918986475509072603988274492338254523919682179700323084167169617716245684540055969194500298976880885466534900490327133434356902533524212744941101469238500990334546197257933040365697281122571898438913033813040027859
q = 2917270228344219924472221188897798789902618263281810355113281879157575741497356945522168552316357276417700368971563177551494320723579146612010452353273237547587402941227901795977981691403950826343318848831462080703
'''
解题思路:
- 这里我们会发现e和q是不互素,不能套用上题模板
- 基本流程依然是:
- AMM算法获得一个根
- 获得所有的ri
- 相乘得到所有的根mp
- 但对于q来说,我们需要将m7看成一个整体,此时1009∣(q-1),所以我们可以按照上面思路求得所有的
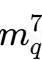 ,然后又有7⊥q,所以可以按照RSA得方式直接解得mq,当然这个顺序不是必须的,你也可以先解e=7的RSA解密步骤,再解e=1009的AMM求根步骤,都没有关系
,然后又有7⊥q,所以可以按照RSA得方式直接解得mq,当然这个顺序不是必须的,你也可以先解e=7的RSA解密步骤,再解e=1009的AMM求根步骤,都没有关系
- 最后我们再将mp和mq的集合俩俩做CRT,得到最终的m
解答:
from Crypto.Util.number import *
from gmpy2 import *
import random
import math
n = 98950849420612859614279452190318782153029931966597217314273823358984928689736597943774367572478091193816498014404387458350141854427041188032441028722132300155987022405432547244436252627801235200799719531840755071562539171489733346246951714886747673950900290905148318965065773167290984966067642777528454814019184856012497536781760044965489668142694134954466581148235162435617572891367282110999553789319439912296241889469226304877
c = 22561646796929363815984273658718096881828574147472740106912668949512978818367595303883956088667384207835022579136977262135029404640598574466248596921339941958216824486529066880854722372158998556902335323841170236300423638675072077074005797219260622119718558697081430219981494670569821476853158740209737420919480047033900157150865588466910802691118334480300332681763467974691587834295938999022060676767513865584039532912503921584
p = 33918986475509072603988274492338254523919682179700323084167169617716245684540055969194500298976880885466534900490327133434356902533524212744941101469238500990334546197257933040365697281122571898438913033813040027859
q = 2917270228344219924472221188897798789902618263281810355113281879157575741497356945522168552316357276417700368971563177551494320723579146612010452353273237547587402941227901795977981691403950826343318848831462080703
e = 1009*7
def onemod(e, q):
p = random.randint(1, q-1)
while(powmod(p, (q-1)//e, q) == 1): # (r,s)=1
p = random.randint(1, q)
return p
def AMM_rth(o, r, q): # r|(q-1
assert((q-1) % r == 0)
p = onemod(r, q)
t = 0
s = q-1
while(s % r == 0):
s = s//r
t += 1
k = 1
while((s*k+1) % r != 0):
k += 1
alp = (s*k+1)//r
a = powmod(p, r**(t-1)*s, q)
b = powmod(o, r*a-1, q)
c = powmod(p, s, q)
h = 1
for i in range(1, t-1):
d = powmod(int(b), r**(t-1-i), q)
if d == 1:
j = 0
else:
j = (-math.log(d, a)) % r
b = (b*(c**(r*j))) % q
h = (h*c**j) % q
c = (c*r) % q
result = (powmod(o, alp, q)*h)
return result
def ALL_Solution(m, q, rt, cq, e):
mp = []
for pr in rt:
r = (pr*m) % q
# assert(pow(r, e, q) == cq)
mp.append(r)
return mp
def calc(mp, mq, e, p, q):
i = 1
j = 1
t1 = invert(q, p)
t2 = invert(p, q)
for mp1 in mp:
for mq1 in mq:
j += 1
if j % 100000 == 0:
print(j)
ans = (mp1*t1*q+mq1*t2*p) % (p*q)
if check(ans):
return
return
def check(m):
try:
a = long_to_bytes(m)
if b'NSSCTF' in a:
print(a)
return True
else:
return False
except:
return False
def ALL_ROOT2(r, q): # use function set() and .add() ensure that the generated elements are not repeated
li = set()
while(len(li) < r):
p = powmod(random.randint(1, q-1), (q-1)//r, q)
li.add(p)
return li
cp = c % p
cq = c % q
mp = AMM_rth(cp, e, p)
mq = AMM_rth(cq, 1009, q)
rt1 = ALL_ROOT2(e, p)
rt2 = ALL_ROOT2(1009, q)
amp = ALL_Solution(mp, p, rt1, cp, e)
amq = ALL_Solution(mq, q, rt2, cq, 1009)
d = invert(7, q-1)
mqs = []
for mq in amq:
mqs.append(pow(mq, d, q))
amq = mqs
calc(amp, amq, e, p, q)
#NSSCTF{827152d9-4ac6-4dd2-8f33-c6a28a1433d2}\x976\x1e\n\xa4#\xa5\x9c\xb8\x7f0\xe7.\xd7>g\xbf'\xce\xdb:_\xf60R\xfc\xdc\xc3\xb7\xcb^\xa3\xad\xda=<\x06\x9b\xcc\x17\xd6_t\x80\x07\xd8\xdaP\xe9\x1f\xe0b\xa5\xf1\xe4\xc0\xe2\xce\xcay\x1bZ\x1e-\xb9\x9f\x82UB\xa0BH\x8c\x8fA\x98E=\n\x10`v\xa2\xed\xa2\x18:\xd9\x9c>A\x82\xac\xed\xb1\x82\xc1TX\x88"
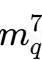 ,然后又有7⊥q,所以可以按照RSA得方式直接解得mq,当然这个顺序不是必须的,你也可以先解e=7的RSA解密步骤,再解e=1009的AMM求根步骤,都没有关系
,然后又有7⊥q,所以可以按照RSA得方式直接解得mq,当然这个顺序不是必须的,你也可以先解e=7的RSA解密步骤,再解e=1009的AMM求根步骤,都没有关系

 浙公网安备 33010602011771号
浙公网安备 33010602011771号