e很大的dp泄露攻击

题目:

from Crypto.Util.number import *

flag = b'NSSCTF{******}' + b'1'*80

p = getPrime(512)
q = getPrime(512)

n = p*q
e = getPrime(128)
d = inverse(e, (p-1)*(q-1))

dp = d % (p-1)

m = bytes_to_long(flag)

c = pow(m, e, n)

print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')
print(f'dp = {dp}')

'''
n = 108280026722298796068968170303156759745471686664814404724171434502249429011870583595808692893118419248225924869164875379709992190884930717654004006466664403479467573176438601715156464950045121937338569942817256182277141174728470067308962244296992229214749863655518517510026063088263849891990324547823192559069
e = 305691242207901867366357529364270390903
c = 26537258289122728220745496185201994733321402056894636636642710319261241111675937946139938310952968353253866895253865273981912174303818938005932883052177988834834575591342856235464380238486868448329727891268391728758132913642966389278296932186703733187105516710825918064228397602264185334108934765627411913661
dp = 2656631506624565349527023729530989647164022271235521672257622068579788839123502046687139927161669209201953909023994372208117081512139181611949631467292513
'''

解题思路:

由欧拉降幂有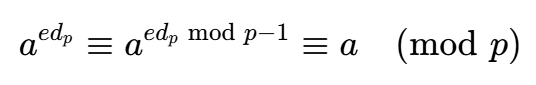

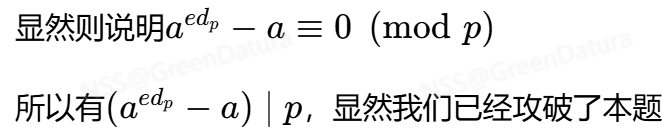
接下来我们需要求解和n的最大公因数即可

当然这里需要注意我们还是有概率失败,一是要保证选取的素数与p互素,这很简单,如果不互素则等于我们已经得到了p的倍数,二是可能结果得到了一个n的倍数,这样最大公因数将会是n,此时我们只需要重新选择a直至得到想要的结果即可

这里的a指本题的m,m可以取10007或2

解答:

from Crypto.Util.number import *
from gmpy2 import *

n = 108280026722298796068968170303156759745471686664814404724171434502249429011870583595808692893118419248225924869164875379709992190884930717654004006466664403479467573176438601715156464950045121937338569942817256182277141174728470067308962244296992229214749863655518517510026063088263849891990324547823192559069
e = 305691242207901867366357529364270390903
c = 26537258289122728220745496185201994733321402056894636636642710319261241111675937946139938310952968353253866895253865273981912174303818938005932883052177988834834575591342856235464380238486868448329727891268391728758132913642966389278296932186703733187105516710825918064228397602264185334108934765627411913661
dp = 2656631506624565349527023729530989647164022271235521672257622068579788839123502046687139927161669209201953909023994372208117081512139181611949631467292513

m = 10007 / m = 2
p = gcd(powmod(m, e*dp, n) - m, n)
q = n // p
d = invert(e, (p - 1) * (q - 1))
m = powmod(c, d, n)
print(long_to_bytes(m))
#NSSCTF{p_leak_but_with_huge_e}11111111111111111111111111111111111111111111111111111111111111111111111111111111