威尔逊定理(筛法的运用)

题目:

#sage
from Crypto.Util.number import bytes_to_long
from sympy import nextprime

FLAG = b'hgame{xxxxxxxxxxxxxxxxxxxxxx}'
m = bytes_to_long(FLAG)

def trick(k):
    if k > 1:
        mul = prod(range(1,k)) 
        if k - mul % k - 1 == 0:
            return euler_phi(k) + trick(k-1) + 1
        else:
            return euler_phi(k) + trick(k-1)
    else:
        return 1

e = 65537
p = q = nextprime(trick(e^2//6)<<128)
n = p * q
enc = pow(m,e,n)
print(f'{enc=}')
#enc=2449294097474714136530140099784592732766444481665278038069484466665506153967851063209402336025065476172617376546

解题思路:

• 首先我们注意到p和q是根据trick函数得到的
• 而这个trick函数其实是个递归函数,直接去算的话计算量还是非常大的[trick(e^2//6=715849728)]
• 注意到prod函数其实是阶乘函数,那么k - mul % k - 1 == 0不就形如威尔逊定理吗
• 要满足威尔逊定理那么k一定是素数,那我们可以直接循环判断递归数是否为素数

def trick_iterative(k):
    result = 1  #初始化结果为1，对应trick(1)
    for i in range(2, k + 1):  #从2开始迭代到k
        if is_prime(i):
            result += euler_phi(i) + 1
        else:
            result += euler_phi(i)
    return result
k = 715849728

• 效率还是有点慢,现在观察return返回值

• 如果k是素数,返回euler_phi(k) + trick(k-1) + 1;如果不是素数,返回euler_phi(k) + trick(k-1)

• 如果k是素数,euler_phi(k)总是等于k - 1;如果k不是素数,euler_phi(k)的值总是小于k - 1

• 因此可以将<font style="color:rgb(6, 6, 7);">trick(k)</font>表示为对于给定的k,首先计算从1到k每个整数i的欧拉函数值euler_phi(i)并将这些值加起来;然后加上不超过k的所有素数的数量π(k)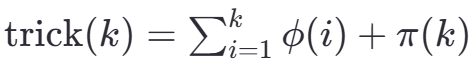

  ![](https://cdn.nlark.com/yuque/0/2025/png/49294098/1738922193447-e7d2a941-4696-45b9-9a29-9cd6501ffeb7.png)
  

def trick_fast(k):
    #计算从1到k的euler_phi值的累加
    euler_sum = sum(euler_phi(i) for i in range(1, k + 1))
    #计算从1到k的素数个数
    prime_count = prime_pi(k)
    #最终结果
    return euler_sum + prime_count
k = 715849728
result = trick_fast(k)
'''
prime_pi(k):计算小于或等于k的素数个数
euler_phi(k):计算小于或等于k的数中与k互质的数的个数
'''

• 思路对了,然后就是优化算法
• 对于非素数,可以利用其质因数分解来快速计算euler_phi;对于素数就直接其本身 - 1
• 最终解得trick(715849728)=155763335447735055,接下来就是常规RSA解密
• 需要注意的是这里p和q相等,所以计算phi时应该是phi = (p - 1) * q而不是(p - 1) * (q - 1)

知识拓展:

威尔逊定理:对于素数k一定有 k − (k−1)! mod k − 1 = 0

威尔逊定理 - OI Wiki

解答:

这个方法效率太低(预计耗时50分钟)，等官方wp

from sage.all import euler_phi, prime_pi, prime_range

def trick_optimized(k):
    # 预计算素数列表
    primes = prime_range(k + 1)
    prime_set = set(primes)
    
    euler_sum = 0
    for i in range(1, k + 1):
        euler_sum += euler_phi(i)
    
    # 素数个数
    prime_count = len(primes)
    #print(prime_count)
    #37030583
    
    # 最终结果
    return euler_sum + prime_count

k = 715849728
result = trick_optimized(k)
print(result)
#155763335447735055

然后就是正常解RSA

from Crypto.Util.number import *
from sympy import nextprime,mod_inverse
p = q = nextprime(155763335447735055<<128)
e=65537
print(p)
#53003516465655400667707442798277521907437914663503790163
enc=2449294097474714136530140099784592732766444481665278038069484466665506153967851063209402336025065476172617376546
n = p * q
phi_n = (p - 1) * q
d = mod_inverse(e, phi_n)
m = pow(enc, d, n)
print(long_to_bytes(m))
#hgame{sieve_is_n0t_that_HArd}

官方wp:(预计耗时4分钟)

在这段代码中,使用了两类不同的筛法:

第一类:素数筛选算法

1. 优化的埃拉托斯特尼筛法(Optimized Sieve of Eratosthenes)

在count_primes_optimized_sieve函数中,使用了优化的埃拉托斯特尼筛法来计算小于或等于n的素数个数,这种方法的核心思想是通过标记合数来找到素数

工作原理:

• 初始化一个布尔数组is_prime,长度为n + 1,所有值初始为True,表示所有数字都被假设为素数
• 将is_prime[0]和is_prime[1]设置为False,因为0和1不是素数
• 从 2 开始,遍历到:
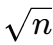  • 如果is_prime[i]是True,则i是一个素数
  • 将i的所有倍数(从i<sup>2</sup>开始)标记为False,因为这些数是合数
• 最后,统计is_prime数组中为True的元素个数,即为小于或等于n的素数个数

第二类:欧拉函数筛选算法

2. 线性筛法计算欧拉函数(Linear Sieve for Euler's Totient Function)

在linear_sieve_phi函数中,使用了线性筛法来计算欧拉函数ϕ(n);欧拉函数ϕ(n)表示小于或等于n的正整数中与n互质的数的个数

工作原理:

• 初始化两个数组:
  • phi:存储每个数的欧拉函数值
  • is_prime:标记是否为素数
• 遍历从 2 到 m 的所有数字:
  • 如果当前数字i是素数,则将其加入素数列表primes,并设置ϕ(i)=i−1
  • 对于每个素数p,更新phi数组:
    • 如果i是p的倍数,则ϕ(i×p)=ϕ(i)×p
    • 否则,ϕ(i×p)=ϕ(i)×(p−1)
• 最后,计算前缀和数组pre_s,其中pre_s[i]是从1到i的欧拉函数值的累加和

3. EulerSumSolver类中的分块筛法(Segmented Sieve)

在EulerSumSolver类的S方法中,使用了分块筛法来高效计算某个范围内的欧拉函数值的累加和;这种方法通过分块处理大范围的数字,避免直接计算每个数字的欧拉函数值,从而提高效率

工作原理:

• 如果n小于或等于预计算的范围m,直接返回前缀和pre_s[n]
• 如果n在缓存中,直接返回缓存结果
• 否则,使用分块筛法:
  • 计算n作为分块的边界
  • 对于每个小于n的数字,递归计算其欧拉函数值的累加和
  • 对于大于n的数字,通过分块计算其欧拉函数值的累加和
• 最后,将所有结果累加并缓存

#筛1(也可以⽤sage内置的prime_pi())
#我感觉sage内置的prime_pi()算这一步更快些
def count_primes_optimized_sieve(n):
    if n < 2:
        return 0
    is_prime = [True] * (n + 1)
    is_prime[0], is_prime[1] = False, False
    for i in range(2, int(n ** 0.5) + 1):
        if is_prime[i]:
            for j in range(i * i, n + 1, i):
                is_prime[j] = False
    return sum(is_prime)
    
print(count_primes_optimized_sieve(65537 ** 2 // 6))
#37030583

#筛2
def linear_sieve_phi(m):
    phi = [0] * (m + 1)
    is_prime = [True] * (m + 1)
    primes = []
    phi[1] = 1
    for i in range(2, m + 1):
        if is_prime[i]:
            primes.append(i)
            phi[i] = i - 1
    for p in primes:
        if i * p > m:
            break
        is_prime[i * p] = False
        if i % p == 0:
            phi[i * p] = phi[i] * p
            break
        else:
            phi[i * p] = phi[i] * (p - 1)
    pre_s = [0] * (m + 1)
    for i in range(1, m + 1):
        pre_s[i] = pre_s[i - 1] + phi[i]
        return phi, pre_s

class EulerSumSolver:
    def __init__(self, m=10 ** 6):
        self.m = m
        self.phi, self.pre_s = linear_sieve_phi(m)
        self.cache = {}

    def S(self, n):
        if n <= self.m:
            return self.pre_s[n]
        if n in self.cache:
            return self.cache[n]
        res = n * (n + 1) // 2
        v = int(n ** 0.5)
        sum1 = 0
        for i in range(2, v + 1):
            sum1 += self.S(n // i)
        u = n // (v + 1)
        sum2 = 0
        for k in range(1, u + 1):
            sum2 += self.S(k) * (n // k - n // (k + 1))
        res -= (sum1 + sum2)
        self.cache[n] = res
        return res

solver = EulerSumSolver(m=10 ** 6)
print(solver.S(65537 ** 2 // 6))
#155763335194435672

然后两个值加起来正常解RSA即可