CRT的进阶使用

题目:

from Crypto.Util.number import *
from secert import flag

m = bytes_to_long(flag)
e = 260792700
q,p,q_,p_ = [getPrime(512) for _ in range(4)]
gift = [q+p,q_+p_]
n,n_ = q*p,q_*p_
mq_ = pow(m,4,q_)
mp_ = pow(m,4,p_)
c = pow(m,e,n)

print(f'mygift={gift}\nmq_={mq_}\nmp_={mp_}\nn={n}\nn_={n_}\nc={c}')
'''
mygift=[15925416640901708561793293991573474917595642805739825596593339102414328214313430010166125066639132916608736569443045051644173933089503934675628814467277922, 18342424676996843423829480445042578097182127446865571536445030052846412665700132683433441858073625594933132038175200824257774638419166516796318527302903098]
mq_=6229615098788722664392369146712291169948485951371133086154028832805750551655072946170332335458186479565263371985534601035559229403357396564568667218817197
mp_=7514598449361191486799480225087938913945061715845128006069296876457814528347371315493644046029376830166983645570092100320566196227210502897068206073043718
n=63329068473206068067147844002844348796575899624395867391964805451897110448983910133293450006821779608031734813916287079551030950968978400757306879502402868643716591624454744334316879241573399993026873598478532467624301968439714860262264449471888606538913071413634346381428901358109273203087030763779091664797
n_=84078907800136966150486965612788894868587998005459927216462899940718213455112139441858657865215211843183780436155474431592540465189966648565764225210091190218976417210291521208716206733270743675534820816685370480170120230334766919110311980614082807421812749491464201740954627794429460268010183163151688591417
c=12623780002384219022772693100787925315981488689172490837413686188416255911213044332780064192900824150269364486747430892667624289724721692959334462348218416297309304391635919115701692314532111050955120844126517392040880404049818026059951326039894605004852370344012563287210613795011783419126458214779488303552
'''

解题思路:

• 根据题目已知条件我们可以很轻松的求出p,q,p',q'

import gmpy2
sum_pq = 15925416640901708561793293991573474917595642805739825596593339102414328214313430010166125066639132916608736569443045051644173933089503934675628814467277922
sum_pq_ = 18342424676996843423829480445042578097182127446865571536445030052846412665700132683433441858073625594933132038175200824257774638419166516796318527302903098
n = 63329068473206068067147844002844348796575899624395867391964805451897110448983910133293450006821779608031734813916287079551030950968978400757306879502402868643716591624454744334316879241573399993026873598478532467624301968439714860262264449471888606538913071413634346381428901358109273203087030763779091664797
n_ = 84078907800136966150486965612788894868587998005459927216462899940718213455112139441858657865215211843183780436155474431592540465189966648565764225210091190218976417210291521208716206733270743675534820816685370480170120230334766919110311980614082807421812749491464201740954627794429460268010183163151688591417
discriminant = sum_pq**2 - 4*n
sqrt_discriminant = gmpy2.isqrt(discriminant)
discriminant_ = sum_pq_**2 - 4*n_
sqrt_discriminant_ = gmpy2.isqrt(discriminant_)
p = (sum_pq + sqrt_discriminant) // 2
q = (sum_pq - sqrt_discriminant) // 2
p_ = (sum_pq_ + sqrt_discriminant_) // 2
q_ = (sum_pq_ - sqrt_discriminant_) // 2
print("p:", p)
print("q:", q)
print("p_:", p_)
print("q_:", q_)
'''
p: 8237763448327424871950828228273863325587732991938648753016149761004918521337676972763871570006722552014080958105888713975090350689060892327170546305946879
q: 7687653192574283689842465763299611592007909813801176843577189341409409692975753037402253496632410364594655611337156337669083582400443042348458268161331043
p_: 9350733807099597101921970461617270659816839029004113803723715480680638784801431578367623576825251918174727017017497634125263419034461866709753181417175321
q_: 8991690869897246321907509983425307437365288417861457732721314572165773880898701105065818281248373676758405021157703190132511219384704650086565345885727777
'''

• 然后因为mq_ = pow(m,4,q_),mp_ = pow(m,4,p_)可以先用中国剩余定理试一试
• 这个e是个偶数,是肯定和p-1,q-1都不互素的
• 分解一下e得到2^2·3·5^2·7^2·113·157
• 正好,他与phi的公因数也是4,因此把e拆开

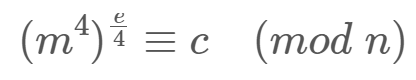
• 然后求e/4对phi的逆元d,正常RSA解密就能得到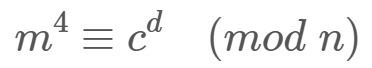

  

• 此时,我们就拥有了关于m^4的三个等式

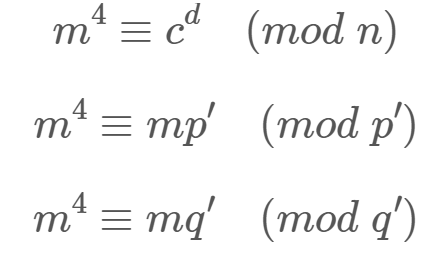
• 中国剩余定理组合,开四次根就能得到flag

解答:

from Crypto.Util.number import *
from gmpy2 import iroot
from sympy.ntheory.modular import crt

e = 260792700
gift=[15925416640901708561793293991573474917595642805739825596593339102414328214313430010166125066639132916608736569443045051644173933089503934675628814467277922, 18342424676996843423829480445042578097182127446865571536445030052846412665700132683433441858073625594933132038175200824257774638419166516796318527302903098]
mq_=6229615098788722664392369146712291169948485951371133086154028832805750551655072946170332335458186479565263371985534601035559229403357396564568667218817197
mp_=7514598449361191486799480225087938913945061715845128006069296876457814528347371315493644046029376830166983645570092100320566196227210502897068206073043718
n=63329068473206068067147844002844348796575899624395867391964805451897110448983910133293450006821779608031734813916287079551030950968978400757306879502402868643716591624454744334316879241573399993026873598478532467624301968439714860262264449471888606538913071413634346381428901358109273203087030763779091664797
n_=84078907800136966150486965612788894868587998005459927216462899940718213455112139441858657865215211843183780436155474431592540465189966648565764225210091190218976417210291521208716206733270743675534820816685370480170120230334766919110311980614082807421812749491464201740954627794429460268010183163151688591417
c=12623780002384219022772693100787925315981488689172490837413686188416255911213044332780064192900824150269364486747430892667624289724721692959334462348218416297309304391635919115701692314532111050955120844126517392040880404049818026059951326039894605004852370344012563287210613795011783419126458214779488303552

p = (iroot((gift[0]**2 - 4*n),2)[0] + gift[0])//2
q = n // p
print(p,q)
#8237763448327424871950828228273863325587732991938648753016149761004918521337676972763871570006722552014080958105888713975090350689060892327170546305946879 7687653192574283689842465763299611592007909813801176843577189341409409692975753037402253496632410364594655611337156337669083582400443042348458268161331043
q_ = (iroot((gift[1]**2 - 4*n_),2)[0] + gift[1])//2
p_ = n_ // q_
print(p_,q_)
#8991690869897246321907509983425307437365288417861457732721314572165773880898701105065818281248373676758405021157703190132511219384704650086565345885727777 9350733807099597101921970461617270659816839029004113803723715480680638784801431578367623576825251918174727017017497634125263419034461866709753181417175321
d = inverse(e//4,(p-1)*(q-1))
m = pow(c,d,n)

N = [n,p_,q_]
C = [m,mp_,mq_]
M = crt(N,C)[0]

print(long_to_bytes(iroot(M,4)[0]))
#0xGame{7881ed67088e9f72b860f8c376599785}