题目:
from gmpy2 import *
from Crypto.Util.number import *
flag = '***************'
p = getPrime(512)
q = getPrime(512)
m1 = bytes_to_long(bytes(flag.encode()))
n = p*q
e1 = getPrime(32)
e2 = getPrime(32)
print()
c1 = pow(m1,e1,n)
c2 = pow(m1,e2,n)
print('c1= '+str(c1))
print('c2= '+str(c2))
print('e1= ' +str(e1))
print('e2= '+str(e2))
print('n= '+str(n))
#c1= 100156221476910922393504870369139942732039899485715044553913743347065883159136513788649486841774544271396690778274591792200052614669235485675534653358596366535073802301361391007325520975043321423979924560272762579823233787671688669418622502663507796640233829689484044539829008058686075845762979657345727814280
#c2= 86203582128388484129915298832227259690596162850520078142152482846864345432564143608324463705492416009896246993950991615005717737886323630334871790740288140033046061512799892371429864110237909925611745163785768204802056985016447086450491884472899152778839120484475953828199840871689380584162839244393022471075
#e1= 3247473589
#e2= 3698409173
#n= 103606706829811720151309965777670519601112877713318435398103278099344725459597221064867089950867125892545997503531556048610968847926307322033117328614701432100084574953706259773711412853364463950703468142791390129671097834871371125741564434710151190962389213898270025272913761067078391308880995594218009110313
解题思路:
- 首先使用扩展欧几里得算法找到两个加密指数e1和e2的最大公约数,并解出方程xe1+ye2=1中的x和y,如果e1和e2互质(即它们的最大公约数gcd为1),那么这个方程一定有整数解
- 一旦我们有了x和y,我们就可以使用它们来计算明文m
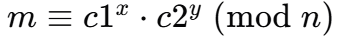
解答:
e1 = 3247473589
n = 103606706829811720151309965777670519601112877713318435398103278099344725459597221064867089950867125892545997503531556048610968847926307322033117328614701432100084574953706259773711412853364463950703468142791390129671097834871371125741564434710151190962389213898270025272913761067078391308880995594218009110313
c1 = 100156221476910922393504870369139942732039899485715044553913743347065883159136513788649486841774544271396690778274591792200052614669235485675534653358596366535073802301361391007325520975043321423979924560272762579823233787671688669418622502663507796640233829689484044539829008058686075845762979657345727814280
e2 = 3698409173
c2 = 86203582128388484129915298832227259690596162850520078142152482846864345432564143608324463705492416009896246993950991615005717737886323630334871790740288140033046061512799892371429864110237909925611745163785768204802056985016447086450491884472899152778839120484475953828199840871689380584162839244393022471075
# 已知两者n相同,e不同,共模攻击
import gmpy2
from Crypto.Util.number import isPrime, sieve_base as primes, long_to_bytes
def egcd(a, b):
if b == 0:
return a, 0;
else:
x, y = egcd(b, a % b)
return y, x - (a // b) * y # 扩展欧几里得算法
s = egcd(e1, e2)
s1 = s[0]
s2 = s[1]
print(s[0], s[1])
#635749796 -558234791
m = gmpy2.powmod(c1, s1, n) * gmpy2.powmod(c2, s2, n) % n
print(long_to_bytes(m))
#NSSCTF{xxxxx******xxxxx}
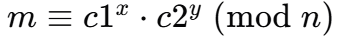


 浙公网安备 33010602011771号
浙公网安备 33010602011771号