题目:
from Crypto.Util.number import *
import gmpy2
flag = b'NSSCTF{******}'
p = getPrime(512)
q = gmpy2.next_prime(p - getPrime(256))
n = p*q
e = 65537
phi = (p-1)*(q-1)
m = bytes_to_long(flag)
c = pow(m, e, n)
print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')
'''
n = 148841588941490812589697505975986386226158446072049530534135525236572105309550985274214825612079495930267744452266230141871521931612761645600600201983605957650711248808703757693378777706453580124982526368706977258199152469200838211055230241296139605912607613807871432800586045262879581100319519318390454452117
e = 65537
c = 69038543593219231496623016705860610154255535760819426453485115089535439537440188692852514795648297200067103841434646958466720891016026061658602312900242658759575613625726750416539176437174502082858413122020981274672260498423684555063381678387696096811975800995242962853092582362805345713900308205654744774932
'''
解题思路:
假设我们有一个合数n,它等于两个素数p和q的乘积,其中p和q非常接近,我们可以写出:
我们寻找两个平方数,它们的差正好等于n,也就是说,我们寻找两个整数a和b,使得:
根据差平方公式,我们可以将上面的等式重写为:
由于p和q非常接近,我们可以假设a是p和q的平均值的整数部分,即:
然后我们计算b为:
如果n可以被分解为两个非常接近的素数的乘积;那么b将是一个整数,我们可以通过a和b来找到p和q:
解答:
from Crypto.Util.number import *
from gmpy2 import *
def fermat_attack(n):
a = isqrt(n)
b2 = a*a - n
b = isqrt(n)
count = 0
while b*b != b2:
a = a + 1
b2 = a*a - n
b = isqrt(b2)
count += 1
p = a+b
q = a-b
assert n == p * q
return p, q
n = 148841588941490812589697505975986386226158446072049530534135525236572105309550985274214825612079495930267744452266230141871521931612761645600600201983605957650711248808703757693378777706453580124982526368706977258199152469200838211055230241296139605912607613807871432800586045262879581100319519318390454452117
e = 65537
c = 69038543593219231496623016705860610154255535760819426453485115089535439537440188692852514795648297200067103841434646958466720891016026061658602312900242658759575613625726750416539176437174502082858413122020981274672260498423684555063381678387696096811975800995242962853092582362805345713900308205654744774932
p, q = fermat_attack(n)
phi = (p-1)*(q-1)
d = invert(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))
#NSSCTF{fermat_factor}

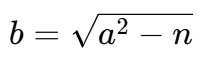

 浙公网安备 33010602011771号
浙公网安备 33010602011771号