城堡（壹）

\[\Huge\mathrm{AGC \; 010} \]

---

\(\Large\text{A. Addition}\)

易得，只有偶数个奇数时可行。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

void solve()
{
	int n, cnt = 0;
	cin >> n;
	for (int i = 1, a; i <= n; i++)
		cin >> a, cnt += (a & 1);
	puts(cnt & 1 ? "NO" : "YES");
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{B. Boxes}\)

先整体考虑，必要 \(\dfrac{n(n + 1)}{2} \mid sum\)，记共 \(k\) 次操作。

加等差数列，考虑差分。一次操作后，\(d_s \gets d_s + (n - 1), \forall i \not= s, d_i \gets d_i - 1\)。在 \(s\) 做 \(x\) 次操作，有 \(d + (n - 1)x - (k - x) = 0\)，即 \(k - d = nx\)。需 \(k - d \geqslant 0 \; \land \; n \mid (k - d)\)。而这是充要的！解出 \(x\) 可以还原。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

const int N = 1e5;

int n;
long long a[N + 5];

void solve()
{
	cin >> n;
	long long sum = 0, base = 1ll * n * (n + 1) / 2;
	for (int i = 1; i <= n; i++)
		cin >> a[i], sum += a[i];

	if (sum % base != 0)
		return puts("NO"), void();
	
	long long t = sum / base;
	a[0] = a[n];
	for (int i = n; i > 0; i--)
		a[i] -= a[i - 1];

	for (int i = 1; i <= n; i++)
	{
		if (t - a[i] < 0 || (t - a[i]) % n != 0)
			return puts("NO"), void();
	}
	return puts("YES"), void();
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{C. Cleaning}\)

点权放边权。考虑每条边被覆盖的次数 \(b_e\)，对叶子 \(a_{u} = b_{<u, f>}\)，对非叶子 \(2a_u = \sum b_{<u, v>}\)。易知可以自底向上推出所有 \(b_e\)，应满足 \(\forall b_e \geqslant 0\)。

只需考虑每个点处能否满足。有 \(\max b_{<u, v>} \leqslant \dfrac{\sum b_{<u,v>}}{2} = a_u\)。

一个经典结论的证明
\(n\) 堆，个数满足 \(0 < a_1 \leqslant a_2 \leqslant \cdots \leqslant a_{n - 1} \leqslant a_n\)，保证总数是 \(2\) 的倍数。不同堆两两配对，则能做到的充要条件是 \(\max a \leqslant \dfrac{\sum a}{2}\)。

• 必要性：反证。若 \(\max a > (\sum a) / 2\)，即 \(\max a\) 大于其余所有数之和，必不满足

• 充分性：每次取最大的两个配对，考虑新的 \(\max\)
  \(\mathrm{i.} \max^\prime = a_n^\prime = a_n - 1\)，有 \(2\max^\prime = 2a_n - 2 \leqslant 2\sum - 2\)

  \(\mathrm{ii.} \max^\prime = a_n\)，即原始 \(a_{n - 2} = a_{n - 1} = a_n\)，则 \(\sum \geqslant 3a_n\)。若不合法，即有 \(2a_n > \sum - 2 \geqslant 3a_n - 2\)，得 \(a_n = 1\)。此时数列全为 \(1\)，又总和为偶数，\(\sum \geqslant 4\) 满足限制。

  故操作后仍合法。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

const int N = 1e5;

int n;
long long a[N + 5];

int root;
vector<int> e[N + 5];

long long b[N + 5];
#define Failed (puts("NO"), exit(0))

void dfs(int u, int fa)
{
	if (e[u].size() == 1)
	{
		b[u] = a[u];
		return ;
	}

	b[u] = a[u] << 1;
	long long mx = 0;

	for (auto v : e[u])
	{
		if (v == fa)
			continue;
		dfs(v, u);
		b[u] -= b[v];
		mx = max(mx, b[v]);
	}

	if (b[u] < 0)
		Failed;

	mx = max(mx, b[u]);
	if (mx > a[u])
		Failed;
	
	if (u == root && b[u] != 0)
		Failed;
	return ;
}

void solve()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
		cin >> a[i];

	for (int i = 1, u, v; i < n; i++)
	{
		cin >> u >> v;
		e[u].push_back(v), e[v].push_back(u);
	}
	for (int i = 1; i <= n; i++)
	{
		if (e[i].size() == 1)
			continue;
		root = i;
		break;
	}

	if (!root)//all nodes are leaf, which is a chain with length 2
		return puts(a[1] == a[2] ? "YES" : "NO"), void();
	dfs(root, 0);//root is not leaf
	return puts("YES"), void();
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{D. Decrementing}\)

考虑奇偶性。当最终不能再除 \(\gcd\) 时，玩家必胜当且仅当有奇数个偶数（因为不能减到 \(0\)）。

只关心奇数、偶数个数的奇偶性，\(\gcd \equiv 1 \pmod{2}\) 对局面无影响。

分讨

• \(\# \operatorname{even} = \operatorname{odd}\) 必胜
  把任意 \(\operatorname{even}\) 减一，有 \(\operatorname{odd}\) 则 \(\gcd\) 为 \(\operatorname{odd}\)。注意到，减之前 \(\gcd = 1\)，则必有其它的 \(\operatorname{odd}\)，因此下家面对 \(\operatorname{even}\) 个 \(\operatorname{even}\) 和至少两个 \(\operatorname{odd}\)。无论如何操作，必得到 \(\operatorname{odd}\) 个 \(\operatorname{even}\) 且 \(\gcd \equiv 1 \pmod{2}\)。局势恢复，以此类推必胜。
• \(\# \operatorname{even} = \operatorname{even} \; \land \; \# \operatorname{odd} \geqslant 2\) 必败
  同上一情况中后手面对的局势。
• \(\# \operatorname{evev} = \operatorname{even} \; \land \; \# \operatorname{odd} = 1\) 未定
  显然不能对偶数操作，否则变为第二种情况。只能令唯一的 \(\operatorname{odd}\) 减一，此时 \(\gcd \equiv 0 \pmod{2}\)，局势不定，交给后手判断。
  每次至少除 \(2\)，至多发生 \(\log V\) 次。

总 \(O(n \log V)\)。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

const int N = 1e5;

int n;
int a[N + 5];

void solve()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
		cin >> a[i];

	if (n == 1)
		return puts(a[1] & 1 ? "Second" : "First"), void();

	int p = 1;
	while (1)
	{
		int odd = 0, even = 0;
		for (int i = 1; i <= n; i++)
		{
			odd += a[i] & 1;
			even += !(a[i] & 1);
		}

		if (even & 1)
			break;
		if (odd > 1)
		{
			p = 3 - p;
			break;
		}

		int index = 0;
		for (int i = 1; i <= n; i++)
		{
			if (a[i] & 1)
			{
				index = i;
				break;
			}
		}

		if (a[index] == 1)
		{
			p = 3 - p;
			break;
		}
		a[index]--;

		int d = a[1];
		for (int i = 2; i <= n; i++)
			d = __gcd(d, a[i]);
		for (int i = 1; i <= n; i++)
			a[i] /= d;

		p = 3 - p;
	}

	puts(p == 1 ? "First" : "Second");
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{E. Rearranging}\)

• 原始做法，未实现，正确性未知

注：开始把二人的目的看反了，下文全是反的

考虑逐位确定。比如第一位。如果 \(\min\) 被移到第一位，意味着 \(\min\) 与前面所有数互质。反之如果有一个不互质的数挡在 \(\min\) 之前，\(\min\) 就不会成为开头。

可以二分！希望挡住 \(\leqslant mid\) 的数怎么办？显然先把 \(> mid\) 的放开头，在此基础上拓展，往后接不互质的数。如果所有数都被遍历到了，即合法！这是一个 \(\operatorname{bfs}\) 的过程。

第二位怎么办？还是二分，但是最先放的应该 \(> mid\) 且与第一个不互质。而其他数要么对第一个有威胁，要么对 \(mid\) 有威胁，都应被拓展而得。

已固定前 \(k\) 位，也是类似的。而新加确定一个数，其他数对前面是否有威胁可以 \(O(n)\) 更新，一些的限制被取 \(\max\)，另一些的限制解除（与新数不互质的那些）。

然而，单次遍历是 \(O(n + m) = O(n^2)\) 的，总 \(O(n^3 \log n)\)。

• 题解做法
  第一步，用不互质的阻挡是对的。但这里已经可以从图论考虑了。不互质的两个数的前后关系，相当于在“不互质图”上给一条边定向。甲操作后，这张图变为一张 \(\operatorname{dag}\)，而乙要最大化拓扑序。

  乙的解法是经典的，用优先队列做拓扑排序。

  考虑甲。对于图上两个不同的连通块，相互独立，甲只能限制块内数的先后顺序。以最小的数为根，按 \(\operatorname{dfs}\) 树定向，其中每个点的出边从小到大遍历。返祖边无影响，因为不把树边走完，后代节点无法入队。

总 \(O(n^2 \log n)\)，其中 \(\log n\) 源自 \(\gcd\)。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

const int N = 2000;

int n;
int a[N + 5];

vector<int> e[N + 5];//undirected

vector<int> g[N + 5];//directed
int in[N + 5];

int vis[N + 5];

void dfs(int u)
{
	vis[u] = 1;
	for (auto v : e[u])
	{
		if (vis[v])
			continue;
		g[u].push_back(v), in[v]++;
		dfs(v);
	}
	return ;
}

void toposort()
{
	priority_queue<int> q;
	for (int i = 1; i <= n; i++)
	{
		if (!in[i])
			q.push(i);
	}

	while (!q.empty())
	{
		int u = q.top();
		q.pop();
		cout << a[u] << " ";

		for (auto v : g[u])
		{
			in[v]--;
			if (!in[v])
				q.push(v);
		}
	}
	cout << endl;
	return ;
}

void solve()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	sort(a + 1, a + n + 1);

	for (int u = 1; u <= n; u++)
	{
		for (int v = 1; v <= n; v++)
		{
			if (__gcd(a[u], a[v]) == 1)
				continue;
			e[u].push_back(v);
			e[v].push_back(u);
		}
	}

	for (int i = 1; i <= n; i++)
	{
		if (!vis[i])
			dfs(i);
	}

	toposort();
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{F. Tree Game}\)

从简单情况入手，其实并没有很复杂。

• 两个点
  \(<u, v>\)，只能来回走，先手在 \(u\) 必胜当且仅当 \(a_u > a_v\)
• 菊花图花心
  先手只能去叶子，后手只能从叶子回来。先手要最快制造一个为 \(0\) 的叶子，显然每次都去最小的那个。必胜当且仅当 \(a_{rt} > \min a_{leaf}\)

一般地，记 \(sg_u\) 表示仅考虑以 \(u\) 为根的子树，先手是否必胜。若从 \(u\) 到 \(v\)：

• \(sg_v = 1\)
  局势变为后手必胜，后手一定会把棋子向 \(v\) 子树内移动。先手必败，故不去。
• \(sg_v = 0\)
  后手必败，只能返回 \(u\)。相当于菊花图叶子。

因此每个点处都类似菊花图花心处理。枚举根，总 \(O(n^2)\)。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

const int N = 3000, Inf = 0x3f3f3f3f;

int n;
int a[N + 5];

vector<int> e[N + 5];

int sg[N + 5];//whether 1st player will win, only consider subtree(u)

void dfs(int u, int fa)
{
	if (fa && e[u].size() == 1)//leaf & not root
		return sg[u] = 0, void();

	int mn = Inf;
	for (auto v : e[u])
	{
		if (v == fa)
			continue;

		dfs(v, u);
		if (sg[v] == 0)
			mn = min(mn, a[v]);
	}

	sg[u] = (a[u] > mn);
	return ;
}

bool check(int rt)
{
	dfs(rt, 0);
	return sg[rt];
}

void solve()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	for (int i = 1, u, v; i < n; i++)
	{
		cin >> u >> v;
		e[u].push_back(v);
		e[v].push_back(u);
	}

	for (int i = 1; i <= n; i++)
	{
		if (check(i))
			cout << i << " ";
	}
	cout << endl;
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\[\Huge\mathrm{AGC \; 011} \]

---

\(\Large\text{A. Airport Bus}\)

贪心。

要超时了，用最少的车接走最早的人，富裕的位置用没走的人补。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <set>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

const int N = 1e5;

int n, c, k;
multiset<int> s;

void solve()
{
	cin >> n >> c >> k;
	for (int i = 1, t; i <= n; i++)
	{
		cin >> t;
		s.insert(t);
	}

	int ans = 0;
	while (!s.empty())
	{
		auto t = *s.begin();
		int lim = t + k, cnt = 0;

		while (!s.empty() && *s.begin() == t)
		{
			cnt++;
			s.erase(s.begin());
		}

		int need = (cnt + c - 1) / c;
		ans += need;

		int rem = need * c - cnt;
		while (!s.empty() && rem > 0 && *s.begin() <= lim)
		{
			rem--;
			s.erase(s.begin());
		}
	}

	cout << ans << endl;
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{B. Colorful Creatures}\)

贪心。

一定是从小到大吃，先吃了小的。倒序维护需要的最小体积 \(need\)，设要吃体积为 \(s\) 的，有

\[\begin{cases} 2 \ need^\prime \geqslant s \\ need^\prime + s \geqslant need \end{cases} \]

即 \(need^\prime = \max\{ need - s, \left\lceil \frac{s}{2} \right\rceil \}\)

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <map>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

const int N = 1e5;

int n;
long long sz[N + 5];
long long sum[N + 5];//prefix sum

void solve()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
		cin >> sz[i];

	sort(sz + 1, sz + n + 1);
	for (int i = 1; i <= n; i++)
		sum[i] = sum[i - 1] + sz[i];

	int ans = 0;
	long long need = 0;
	for (int i = n; i > 0; i--)
	{
		ans += (sum[i] >= need);
		need = max(need - sz[i], (sz[i] + 1) >> 1);
	}
	cout << ans << endl;
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{C. Squared Graph}\)

打表。

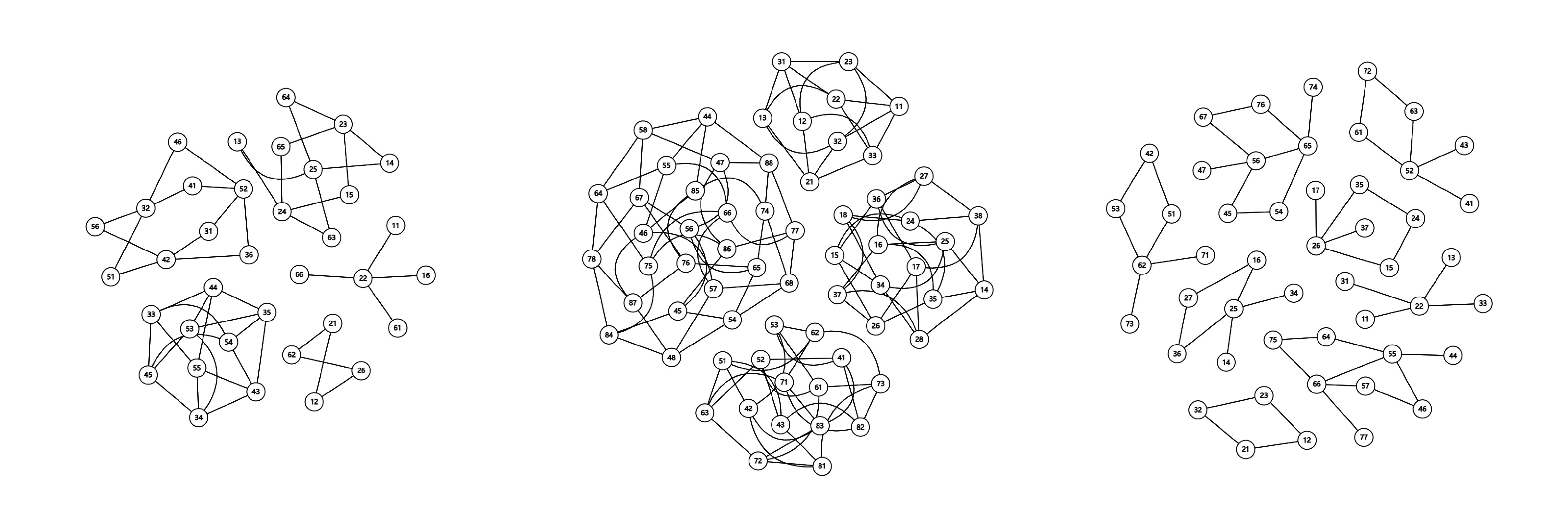
不妨先对每个连通块考虑。

考虑一条边 \(<u, v>\)，在 \((u, *)\) 和 \((v, *)\) 这些点中，每条边 \(<x, y>\) 会对应两条边：\((u, x) \sim (v, y)\) 与 \((u, y) \sim (v, x)\)。因此粗略来看，一个连通块会对应两个新连通块。有时这两个会彼此联通成为一个大连通块。如图，一条左上-右下的边与左下-右上的边相连，也即每条边所连的边是不同“性质”的，这里有二分图的意思了！

• 对于二分图，一定是两个块
• 对于非二分图，一定是一个块。首先这对奇环成立，然后考虑从环上伸出的边，十字结构都与环连通，进而推出整个块连通

注：下图省略了一些边

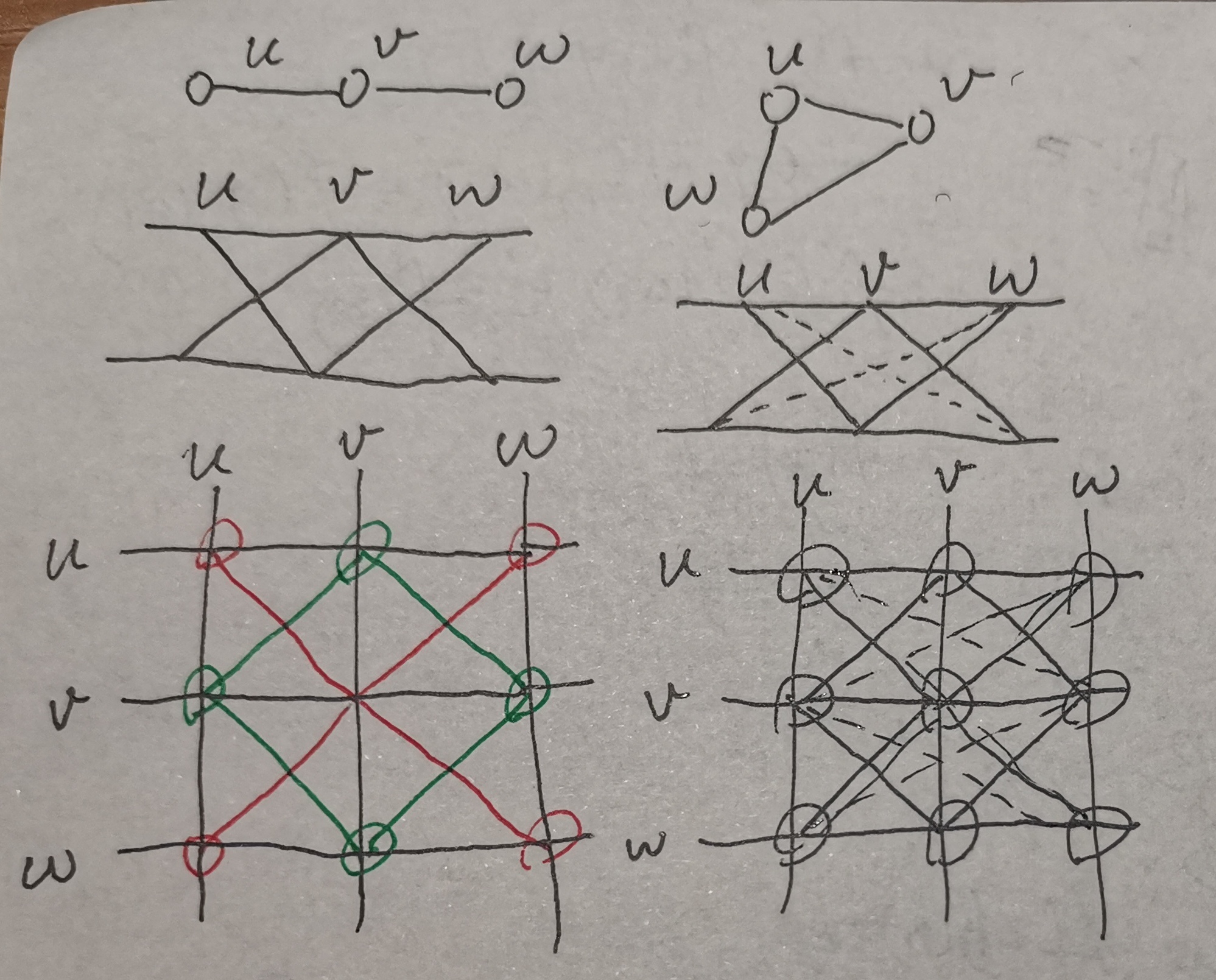
现在单个连通块的情况研究清楚了，接下来考虑不同块间的影响。

如下面第一张图，从左到右，前两张图为二分图与非二分图，第三张为两个二分图；第二张图为对应的新图

从坐标考虑，新图关于主对角线对称，任意两个原图连通块可以组成若干个新图连通块，新连通块大小为原连通块大小之乘积。容易发现：

• 二分图 \(\times\) 二分图 \(\to\) \(4\) 个块
• 二分图 \(\times\) 非二分图 \(\to\) \(2\) 个块
• 非二分图 \(\times\) 非二分图 \(\to\) \(1\) 个块

注意一下，当原连通块为孤立点时，结论可能有偏差，此时特判就好了。孤立点不会产生任何新连通块。

最后，答案怎么计算呢？反向思考，考虑比 \(n^2\) 少了多少。一个大小为 \(sz\) 的新连通块会带来 \(sz - 1\) 的损失。结合上述观察，可以边寻找连通块边计算。见代码。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

const int N = 1e5;

int n, m;
vector<int> e[N + 5];

int sz[N + 5], col[N + 5];

bool dfs(int u)
{
	sz[u] = 1;
	bool res = 1;
	for (auto v : e[u])
	{
		if (!col[v])
		{
			col[v] = 3 - col[u];
			res &= dfs(v);
			sz[u] += sz[v];
		}
		else
			res &= (col[u] != col[v]);
	}
	return res;
}

void solve()
{
	cin >> n >> m;
	for (int i = 1, u, v; i <= m; i++)
	{
		cin >> u >> v;
		e[u].push_back(v);
		e[v].push_back(u);
	}

	long long ans = 1ll * n * n;
	int cnt_bi = 0, cnt_none = 0;
	int sz_bi = 0, sz_none = 0;
	
	for (int u = 1; u <= n; u++)
	{
		if (col[u])
			continue;

		col[u] = 1;
		bool res = dfs(u);
		if (sz[u] == 1)
			continue;

		ans -= 1ll * sz[u] * sz[u] - 1 - res;
		ans -= 2ll * sz[u] * sz_bi - 2 * (1 + res) * cnt_bi;
		ans -= 2ll * sz[u] * sz_none - 2 * cnt_none;

		if (res)
			cnt_bi++, sz_bi += sz[u];
		else
			cnt_none++, sz_none += sz[u];
	}
	cout << ans << endl;
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{D. Half Reflector}\)

还是打表！

放一个简易可视化打表机，具体的表就不放了

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
#define LOCAL
// #define TestCases

const int N = 100;

int n, k;
int s[N + 5];

void print(int pos, int v)
{
	if (pos == 0 && v == -1)
		printf(" <- ");
	else if (pos == 1 && v == 1)
		printf(" -> ");
	else
		printf("    ");

	for (int i = 1; i <= n; i++)
	{
		printf("%d", s[i]);
		if (pos == i && v == -1)
			printf(" <- ");
		else if (pos == i + 1 && v == 1)
			printf(" -> ");
		else
			printf("    ");
	}
	printf("\n");
	return ;
}
void stimulate()
{
	int pos = 1, v = 1;
	print(pos, v);

	while (0 < pos && pos <= n)
	{
		if (s[pos])
		{
			s[pos] ^= 1;
		}
		else
		{
			s[pos] ^= 1;
			v *= -1;
		}
		pos += v;

		print(pos, v);
	}
	return ;
}

void solve()
{
	cin >> n >> k;
	for (int i = 1; i <= n; i++)
	{
		char c;
		cin >> c;
		s[i] = c - 'A';
	}

	k = 100;
	for (int r = 1; r <= k; r++)
	{
		printf("Round: %d\n", r);
		stimulate();
		printf("\n");
	}
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

从一些极端情况入手，比如看看 \(10\) 个或者 \(9\) 个 \(\text{A}\) 或 \(\text{B}\) 会怎么样。发现很快会出现循环，而且奇偶性确实有影响。

具体来讲：

• 球要么被第一个字母弹回，要么从最右端飞出
• \(\text{A...A} \to \text{BA...A} \to \text{B...BA}\)
• \(\text{B...B} \to \text{A...A}\) 化为上面的情况
• 对任意 \(n\)，至多 \(2n\) 轮后一定出现循环，且能取等
  \(n \equiv 0 \pmod{2}\)，稳定为 \(\text{BABA...BABA}\)
  \(n \equiv 1 \pmod{2}\)，稳定为 \(\text{ABABA...BA} \leftrightarrow \text{BBABA...BA}\)，以 \(2\) 为周期

\(2n\) 的系数 \(2\) 从何而来？不难发现，第一个字母交替出现 \(\text{A, B}\)，因此只有一半的时候球可以横穿整个串。

再详细分析具体过程，以 \(\text{AAAAABBBBBAAAAABBBBB}\) 为例，下文 \(0 = \text{A}, 1 = \text{B}\)

过程

Begin:
0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 

Round: 1
1 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 

Round: 2
1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 

Round: 3
0 0 0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 1 0 

Round: 4
1 0 0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 1 0 

Round: 5
1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 1 0 

Round: 6
0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 1 0 1 0 

Round: 7
1 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 1 0 1 0 

Round: 8
0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 1 0 1 0 

Round: 9
1 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 1 0 1 0 

Round: 10
1 1 1 1 0 0 0 0 0 1 1 1 1 1 1 0 1 0 1 0 

Round: 11
0 0 0 1 1 1 1 1 0 0 0 0 0 0 1 0 1 0 1 0 

Round: 12
1 0 0 1 1 1 1 1 0 0 0 0 0 0 1 0 1 0 1 0 

Round: 13
1 1 0 0 0 0 0 1 1 1 1 1 1 0 1 0 1 0 1 0 

Round: 14
0 1 1 1 1 1 0 0 0 0 0 0 1 0 1 0 1 0 1 0 

Round: 15
1 1 1 1 1 1 0 0 0 0 0 0 1 0 1 0 1 0 1 0 

Round: 16
0 0 0 0 0 1 1 1 1 1 1 0 1 0 1 0 1 0 1 0 

Round: 17
1 0 0 0 0 1 1 1 1 1 1 0 1 0 1 0 1 0 1 0 

Round: 18
1 1 1 1 0 0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 

Round: 19
0 0 0 1 1 1 1 1 1 0 1 0 1 0 1 0 1 0 1 0 

Round: 20
1 0 0 1 1 1 1 1 1 0 1 0 1 0 1 0 1 0 1 0 

Round: 21
1 1 0 0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 

Round: 22
0 1 1 1 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 

Round: 23
1 1 1 1 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 

Round: 24
0 0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 

Round: 25
1 0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 

Round: 26
1 1 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 

Round: 27
0 0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 

Round: 28
1 0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 

Round: 29
1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 

Round: 30
0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 

Round: 31
1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 

发现一次横穿操作后，每个连续段向前移动一位且字母翻转，对于后端空出来的部分，交替填入两种字母且不再改变（也可以看作连续段，和前面规律类似）。

显然可以用双端队列模拟！记录当前相对初始有没有翻转，每次模拟是 \(O(1)\) 的。先模拟 \(2n\) 轮，然后统一按 \(2\) 为周期计算。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <queue>
#include <string>
#include <map>
#include <vector>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

const int N = 2e5;

int n, k;
string s;

typedef pair<int, int> node;
#define col first//0: A, 1: B
#define len second

deque<node> q;
vector<int> v;

/*
stable:
even: BA...BA
odd ABA...BA <-> BBA...BA
*/

void solve()
{
	cin >> n >> k >> s;

	for (int l = 0, r = 0; l < n; l = r + 1)
	{
		r = l;
		while (r + 1 < n && s[r + 1] == s[r])
			r++;
		q.emplace_back(s[l] - 'A', r - l + 1);
	}

	int flip = 0;
	for (int r = 1; r <= n + n && !q.empty() && k; r++, k--)
	{
		auto info = q.front();
		q.pop_front();

		if ((info.col ^ flip) == 0)//A -> B
		{
			if (info.len == 1)//A BBB -> BBBB
			{
				if (q.empty())
				{
					v.push_back(1);
					continue;
				}

				info = q.front();
				q.pop_front();
				info.len++;
				q.push_front(info);
			}
			else//AAA -> B AA
			{
				info.len--;
				q.push_front(info);
				q.emplace_front(1 ^ flip, 1);
			}
			continue;
		}

		info.len--;//BBB (BAAA) -> AAA (BBB A)
		if (info.len > 0)
			q.push_front(info);

		if (!v.empty())
			v.push_back(v.back() ^ 1);
		else//q can't be empty
		{
			info = q.back();
			if ((info.col ^ flip) == 0)//only if end with A
				v.push_back(0);
			else
			{
				if (info.len != n)//not all B -> #(A) + 1
				{
					info.len++;
					q.pop_back();
					q.push_back(info);
				}
			}
		}
		flip ^= 1;
	}

	reverse(v.begin(), v.end());
	if (!k)
	{
		while (!q.empty())
		{
			auto info = q.front();
			q.pop_front();

			while (info.len--)
				cout << char((info.col ^ flip) + 'A');
		}
		for (auto c : v)
			cout << char(c + 'A');
		cout << endl;
		return ;
	}

	k %= 2;
	if ((n & 1) && (k & 1))
		v[0] ^= 1;

	for (auto c : v)
		cout << char(c + 'A');
	cout << endl;
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{E. Increasing Numbers}\)

猜了神秘结论，过了

我的做法：猜测可以贪心，每次减去最大的“不降数”

本来只是拿样例 20170312 手玩一下，发现这个是对的。写了 \(\text{python}\) 验证，样例全过了。
讨论区有人认为，该结论和从官方解法构造答案本质相同，但这对我并不显然。
大胆猜想，对任意进制结论均成立，然而我哪个都不会证明。

实现上，先找到 \(n\) 的最长不降前缀，再在该前缀末尾连续段的首位减一，首位后用 \(9\) 填满。相当于先抹去一段前缀，再 +1。
\(\text{e.g. 20170312 = 19999999 + 170313 = 19999999 + 169999 + 314 = 19999999 + 169999 + 299 + 15}\)

写了一棵线段树维护。但其实暴力就是对的，+1 操作均摊常数，找前缀可能需要一点优化，但线段树大抵是不用的了。
另外，由此可知答案不超过位数，因为每次一定抹去最高位。若 +1 导致进位到最高位，则后面必须全为 \(9\)，又与最大矛盾了。

$\text{python}$ 验证

n = int(input())

tot = len(str(n))

cnt = 0
while n > 0:
    cnt = cnt + 1
    
    delta = str("")

    s = "0" + str(n)
    l = len(s) - 1

    pos = 1
    while pos + 1 <= l and s[pos + 1] >= s[pos]:
        pos = pos + 1

    lis = pos + tot - l

    if pos == l:
        break

    lenlen = 1

    while pos > 0 and s[pos - 1] == s[pos]:
        pos = pos - 1
        lenlen = lenlen + 1

    if pos == 0:
        delta = delta + str(int(s[1]) - 1)
        for i in range(2, l + 1):
            delta = delta + str(9)
    else:
        for i in range(1, pos):
            delta = delta + str(s[i])
        delta = delta + str(int(s[pos]) - 1)
        for i in range(pos + 1, l + 1):
            delta = delta + str(9)

    delta = int(delta)
    n = n - delta

    zero = tot - len(str(n))
    delta = ""
    for i in range(1, zero + 1):
        delta = delta + "0"
    delta = delta + str(n)
    print(delta)

print(cnt)

官方做法是合理的。

首先，任何一个“不降数”都可以拆成至多 \(9\) 个形如 \(\overline{1...1}\) 数之和。而 \(\overline{1...1} = \dfrac{10^k - 1}{9}\)，对 \(0\) 也满足，故不妨认为每个数都拆成 \(9\) 个形如 \(\dfrac{10^k - 1}{9}\)的数

\(n = \sum\limits_{i = 1}^{ans} \sum\limits_{j = 1}^{9} \dfrac{10^k - 1}{9}\)

\(\implies 9n + 9ans = \sum\limits_{i - 1}^{9ans} 10^k\)

右式共 \(9ans\) 个 \(1\)，则左式数字和必不超过 \(9ans\)。每进位一次，数字和减少 \(9\)，而两边均为 \(9\) 的倍数，无需考虑。只用从小到大枚举 \(ans\)，暴力维护进位和数字和即可，仍然是均摊的。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

const int N = 5e5, SZ = N << 2;

int n;
string str;

struct Node
{
	int keyl, keyr;
	int lis, len;//left, right
	int full;//r - l + 1
	int tag;

	Node(): tag(-1) {}
};
Node node[SZ + 5];

#define ls(p) (p << 1)
#define rs(p) (p << 1 | 1)
#define keyl(p) node[p].keyl
#define keyr(p) node[p].keyr
#define lis(p) node[p].lis
#define len(p) node[p].len
#define full(p) node[p].full
#define tag(p) node[p].tag

void pushup(int p)
{
	keyl(p) = keyl(ls(p)), keyr(p) = keyr(rs(p));

	if (lis(ls(p)) == full(ls(p)))
		lis(p) = full(ls(p)) + (keyr(ls(p)) <= keyl(rs(p))) * lis(rs(p));
	else
		lis(p) = lis(ls(p));

	if (len(rs(p)) == full(rs(p)))
		len(p) = full(rs(p)) + (keyr(ls(p)) == keyl(rs(p))) * len(ls(p));
	else
		len(p) = len(rs(p));
	return ;
}

void cover(int p, int x)
{
	tag(p) = x;
	keyl(p) = keyr(p) = x;
	lis(p) = len(p) = full(p);
	return ;
}
void pushdown(int p)
{
	if (tag(p) > -1)
	{
		cover(ls(p), tag(p));
		cover(rs(p), tag(p));
		tag(p) = -1;
	}
	return ;
}

void build(int p, int l, int r)
{
	full(p) = r - l + 1;
	if (l == r)
	{
		keyl(p) = keyr(p) = str[l - 1] - '0';
		lis(p) = len(p) = 1;
		return ;
	}

	int mid = (l + r) >> 1;
	build(ls(p), l, mid);
	build(rs(p), mid + 1, r);
	pushup(p);
	return ;
}

Node operator + (Node x, Node y)
{
	Node z;
	z.keyl = x.keyl, z.keyr = y.keyr;
	z.full = x.full + y.full;

	z.len = y.len;
	if (y.len == y.full && x.keyr == y.keyl)
		z.len += x.len;
	return z;
}
Node query(int p, int l, int r, int L, int R)
{
	if (L <= l && r <= R)
		return node[p];

	int mid = (l + r) >> 1;
	pushdown(p);
	if (R <= mid)
		return query(ls(p), l, mid, L, R);
	if (L > mid)
		return query(rs(p), mid + 1, r, L, R);
	return query(ls(p), l, mid, L, R) + query(rs(p), mid + 1, r, L, R);
}

int get(int p, int l, int r, int pos)
{
	if (l == r)
		return keyl(p);

	int mid = (l + r) >> 1;
	pushdown(p);
	if (pos <= mid)
		return get(ls(p), l, mid, pos);
	return get(rs(p), mid + 1, r, pos);
}

void modify(int p, int l, int r, int L, int R, int x)
{
	if (L <= l && r <= R)
		return cover(p, x), void();

	int mid = (l + r) >> 1;
	pushdown(p);
	if (L <= mid)
		modify(ls(p), l, mid, L, R, x);
	if (R > mid)
		modify(rs(p), mid + 1, r, L, R, x);
	pushup(p);
	return ;
}

void solve()
{
	cin >> str;

	n = str.size();
	build(1, 1, n);

	int ans = 1;
	while (lis(1) < n)
	{
		int split = lis(1);

		auto res = query(1, 1, n, 1, split);
		int len = res.len;
		
		modify(1, 1, n, 1, split - len + 1, 0);

		if (keyr(1) < 9)
			modify(1, 1, n, n, n, keyr(1) + 1);
		else
		{
			int pos = n - len(1);
			int x = get(1, 1, n, pos);

			modify(1, 1, n, pos, pos, x + 1);
			modify(1, 1, n, pos + 1, n, 0);
		}

		ans++;
	}
	cout << ans << endl;
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{F. Train Service Planning}\)

本场唯一没有独立想出的题。

容易发现，对任意车站、任意方向，都是每 \(k\) 个单位发车一辆。

先考虑判断无解。对于单行线，\(k\) 时间内至少双向各发车一辆，故 \(k \geqslant 2a_i\) 是必要的。而满足所有限制也一定存在合法方案，无非是列车在每一站停得长一点。

设 \(\{p_n\}, \{q_n\}\) 表示 \(0 \to n\) 和 \(n \to 0\) 在每一站停留的时间（下标为车站编号，非停留的车站序数），总可以通过调整在始发站、终点站的时间使总全程为 \(k\) 的倍数。题意即要求最小化总停留时间。

记 \(\{t_n\}, \{f_n\}, \{g_n\}\) 为 \(a, p, q\) 的前缀和。对于 \(i - 1 \to i\)，考虑两个方向的占用的时间，需要在模 \(k\) 意义下恒不交。

• \(0 \to n\)
  \((t_{i - 1} + f_{i - 1}, \; t_i + f_{i - 1})\)
• \(n \to 0\)
  \((t_n - t_i + g_n - g_{i - 1}, \; t_n - t_{i - 1} + g_n - g_{i - 1})\)
  \(\xrightarrow{\mod k} (-t_i - g_{i - 1}, \; -t_{i - 1} - g_{i - 1})\)

恒无交，即要求：

\[\begin{cases} t_{i - 1} &+ f_{i - 1} &+ \lambda k &\not\in (-t_i - g_{i - 1}, \; -t_{i - 1} - g_{i - 1}) \\ t_i &+ f_{i - 1} &+ \lambda k &\not\in (-t_i - g_{i - 1}, \; -t_{i - 1} - g_{i - 1}) \\ -t_i &- g_{i - 1} &+ \lambda k &\not\in (t_{i - 1} + f_{i - 1}, \; t_i + f_{i - 1}) \\ -t_{i - 1} &- g_{i - 1} &+\lambda k &\not\in (t_{i - 1} + f_{i - 1}, \; t_i + f_{i - 1}) \end{cases} \]

化简得 \(f_i + g_i + \lambda k \not\in (-2t_i, -2t_{i - 1})\)

这也侧面说明了无解条件的合理性。如果区间长度超过 \(k\)，则必存在 \(\lambda\) 使 \(f_i + g_i\) 落入区间中。

记 \(x = f_i + g_i\)。初始 \(x\) 任意，每次给出一个模意义下的区间，让 \(x\) 加上一非负值使之不在区间内，最小化加的数之和。

显然存在一种最优解，\(x\) 只取区间端点值。

记 \(dp_i\) 表示现在 \(x = i\) 加的数最小和。区间内的 \(dp\) 只能转移到右端点（因为加的数非负），\(dp_r \gets dp_i + r - i\) 或 \(dp_r \gets dp_i + k + r - i\)，视区间是否跨过 \(k\) 而定。区间内 \(dp_i\) 赋为 \(\infty\)。线段树维护区间 \(dp_i - i\) 最小值。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

const int N = 1e5;
const int L = N * 2 + 2;

int n;
long long k;
long long t[N + 5];
int b[N + 5];

long long tmp[L + 5];
int cnt;

const int SZ = L << 2;
const long long Inf = 1e16;

struct Node
{
	long long key;
	int tag;
};
Node node[SZ + 5];

#define ls(p) (p << 1)
#define rs(p) (p << 1 | 1)
#define key(p) node[p].key
#define tag(p) node[p].tag

void pushup(int p)
{
	key(p) = min(key(ls(p)), key(rs(p)));
	return ;
}

void cover(int p)
{
	tag(p) = 1;
	key(p) = Inf;
	return ;
}
void pushdown(int p)
{
	if (tag(p))
	{
		cover(ls(p));
		cover(rs(p));
		tag(p) = 0;
	}
	return ;
}

void build(int p, int l, int r)
{
	if (l == r)
		return key(p) = -tmp[l], void();

	int mid = (l + r) >> 1;
	build(ls(p), l, mid);
	build(rs(p), mid + 1, r);
	pushup(p);
	return ;
}

void modify(int p, int l, int r, int pos, long long val)
{
	if (l == r)
		return key(p) = min(key(p), val), void();

	int mid = (l + r) >> 1;
	pushdown(p);

	if (pos <= mid)
		modify(ls(p), l, mid, pos, val);
	else
		modify(rs(p), mid + 1, r, pos, val);

	pushup(p);
	return ;
}
void clr(int p, int l, int r, int L, int R)
{
	if (L <= l && r <= R)
		return cover(p), void();

	int mid = (l + r) >> 1;
	pushdown(p);

	if (L <= mid)
		clr(ls(p), l, mid, L, R);
	if (R > mid)
		clr(rs(p), mid + 1, r, L, R);

	pushup(p);
	return ;
}
long long query(int p, int l, int r, int L, int R)
{
	if (L <= l && r <= R)
		return key(p);

	int mid = (l + r) >> 1;
	pushdown(p);

	long long res = Inf;
	if (L <= mid)
		res = min(res, query(ls(p), l, mid, L, R));
	if (R > mid)
		res = min(res, query(rs(p), mid + 1, r, L, R));
	return res;
}

long long dfs(int p, int l, int r)
{
	if (l == r)
		return key(p) + tmp[l];

	int mid = (l + r) >> 1;
	pushdown(p);

	long long res = Inf;
	res = min(res, dfs(ls(p), l, mid));
	res = min(res, dfs(rs(p), mid + 1, r));
	return res;
}

void solve()
{
	cin >> n >> k;
	auto mod = [&](long long val)
	{
		return (val % k + k) % k;
	};

	for (int i = 1; i <= n; i++)
	{
		cin >> t[i] >> b[i];
		if (b[i] == 1 && t[i] + t[i] > k)
			return puts("-1"), void();
		t[i] += t[i - 1];

		tmp[++cnt] = mod(-2 * t[i]);//l
		tmp[++cnt] = mod(-2 * t[i - 1]);//r
	}
	tmp[++cnt] = 0;
	tmp[++cnt] = k - 1;

	sort(tmp + 1, tmp + cnt + 1);
	cnt = unique(tmp + 1, tmp + cnt + 1) - tmp - 1;

	build(1, 1, cnt);
	for (int i = 1; i <= n; i++)
	{
		if (b[i] == 2)
			continue;

		int l = lower_bound(tmp + 1, tmp + cnt + 1, mod(-2 * t[i])) - tmp;
		int r = lower_bound(tmp + 1, tmp + cnt + 1, mod(-2 * t[i - 1])) - tmp;

		if (l < r)//l = r -> [r + 1, cnt] + [1, l - 1] is illegal
		{
			long long res = query(1, 1, cnt, l + 1, r - 1);
			modify(1, 1, cnt, r, res);
			clr(1, 1, cnt, l + 1, r - 1);
		}
		else
		{
			long long res = Inf;
			if (l + 1 <= cnt)
			{
				res = query(1, 1, cnt, l + 1, cnt) + k;
				clr(1, 1, cnt, l + 1, cnt);
			}
			if (r - 1 > 0)
			{
				res = min(res, query(1, 1, cnt, 1, r - 1));
				clr(1, 1, cnt, 1, r - 1);
			}
			modify(1, 1, cnt, r, res);
		}
	}

	long long ans = 2 * t[n] + dfs(1, 1, cnt);
	cout << ans << endl;
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\[\Huge\mathrm{AGC \; 012} \]

---

\(\Large\text{A. AtCoder Group Contest}\)

先升序排序，考虑贪心。最大的 \(t\) 个元素中，最多选出 \(\lfloor \frac{t}{2} \rfloor\) 个，因为若中位数出现了，最大值也必出现。

归纳可得，答案即为 \(a_{3n - 1} + a_{3n - 3} + \cdots\)

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

const int N = 1e5, M = N * 3;

int n, m;
int a[M + 5];

void solve()
{
	cin >> n;
	m = n * 3;
	for (int i = 1; i <= m; i++)
		cin >> a[i];

	sort(a + 1, a + m + 1);
	long long ans = 0;
	for (int i = 1, j = m - 1; i <= n; i++, j -= 2)
		ans += a[j];
	cout << ans << endl;
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{B. Splatter Painting}\)

一个直接的想法是，应该从后往前执行操作，希望每个点只被染一次。

图上一个点的领域没有什么好的维护方法，大概只能暴力扩展，那么应以减少无效操作入手。对于 \(u\)，依次执行半径为 \(d, d'\) 的操作，则 \(d \geqslant d'\) 时前一次操作的对象完全覆盖后一次，也即后一次可以忽略。因此，一个点最多被操作 \(11\) 次。

维护每个点的最大半径，双端队列 \(\text{bfs}\)

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
#include <queue>
#include <tuple>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

constexpr int N = 1e5;

int n, m, q;
vector<int> e[N + 5];

int dfn[N + 5], col[N + 5];

typedef tuple<int, int, int> Info;
deque<Info> dq;

void solve()
{
	cin >> n >> m;
	for (int i = 1, u, v; i <= m; i++)
	{
		cin >> u >> v;
		e[u].push_back(v), e[v].push_back(u);
	}

	cin >> q;
	for (int i = 1, u, d, c; i <= q; i++)
	{
		cin >> u >> d >> c;
		dq.emplace_front(u, d, c);
	}

	memset(dfn, -1, sizeof(dfn));
	while (!dq.empty())
	{
		int u, d, c;
		tie(u, d, c) = dq.front();
		dq.pop_front();

		if (!col[u])
			col[u] = c;
		dfn[u] = d;

		d--;
		if (d < 0)
			continue;

		for (auto v: e[u])
		{
			if (dfn[v] < d)
				dq.emplace_front(v, d, c);
		}
	}

	for (int i = 1; i <= n; i++)
		cout << col[i] << endl;
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{C. Tautonym Puzzle}\)

非常正确的随机化，拜谢 \(\text{10circle}\) 老师的题解。

两个字符集无交的字符串拼起来，好串数也是相加。考虑随机一些短字符串凑出 \(n\)。
首先应该手搓一个 \(\text{spj}\)。

枚举第二个子序列的开头 \(s\)，设 \(f(e_1, e_2)\) 表示两个子序列依次以 \(str_{e_1}, str_{e_2}\) 结尾的合法串数量。

\[\begin{cases} f(e_1, s) = 1 \; &str_{e_1} = str_s \\ f(e_1, e_2) \to f(e_1', e_2') \; &str_{e_1'} = str_{e_2'} \land e_1 < e_1' < s < e_2 < e_2' \end{cases} \]

观察转移，\(f(e_1', e_2')\) 其实相当于一个以 \((e_1' - 1, e_2' - 1)\) 为顶点的矩形内所有 \(f\) 之和（\(-1\) 因为上面是严格小于），可以边 \(\text{dp}\) 边维护矩形前缀和，单次是 \(O(len^2)\) 的
总 \(O(len^3)\)。合法串数即 \(\sum\limits_{s = 2}^{len} \sum\limits_{e_1, e_2} f(e_1, e_2)\)，如果过程中串数已经大于 \(n\) 可以直接返回避免爆长整型

\(n\) 很大，串长限制较紧，肯定希望单串的”性价比“尽量高。这意味着，串长要短，字符集 \(|\sum|\) 要小。
\(|\sum| = 1\) 好不好呢？简单计算知，长为 \(len\) 的有 \(2^{len - 1}\) 个合法串。而用二进制拆分来凑，总长度会爆 \(200\)，原因是增长过快而不实用。
尝试 \(|\sum| = 2\)，每一位等概率在 \({0, 1}\) 随机，发现当 \(len = 50\) 时平均合法个数已达到 \(10^{11}\) 量级，够用了。
当然合法个数较少的串同样重要，用来补缺。
因此，考虑 \(\forall len = 2, 3, \cdots, 50\)，每个长度随机 \(400\) 个并计算。求解用贪心，每次选一个最大的减掉。该做法在极限情况下需要 \(180 \sim 190\) 位，擦边球但确实能稳定通过。
还是执着于确定性做法？很简单，用固定的随机种子就好了！比如某八位质数。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
#include <random>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

constexpr int S = 200;
constexpr long long Lim = 1e12;
constexpr int Size = 2e4;

typedef vector<int> arr;

namespace Calc
{
	long long f[S + 5][S + 5];
	long long pre[S + 5][S + 5];

	long long calc(arr a)
	{
		long long sum = 0;
		int len = a.size();

		for (int s = 2; s <= len; s++)//start
		{
			for (int e1 = 1; e1 < s; e1++)
				f[e1][s] = (a[e1 - 1] == a[s - 1]);

			for (int e1 = 1; e1 < s; e1++)
			for (int e2 = s; e2 <= len; e2++)
			{
				if (a[e1 - 1] == a[e2 - 1])
					f[e1][e2] += pre[e1 - 1][e2 - 1];
				pre[e1][e2] = f[e1][e2] + pre[e1 - 1][e2] + pre[e1][e2 - 1] - pre[e1 - 1][e2 - 1];

				sum += f[e1][e2];
				if (sum > Lim)
					return Lim + 1;
			}

			for (int e1 = 1; e1 < s; e1++)
			for (int e2 = s; e2 <= len; e2++)
				f[e1][e2] = pre[e1][e2] = 0;
		}

		return sum;
	}
}
using Calc :: calc;

namespace Gen
{
	mt19937 rnd(19260817);

	arr generate(int len)
	{
		arr v(len);
		for (int i = 0; i < len; i++)
			v[i] = rnd() & 1;
		return v;
	}
}
using Gen :: generate;

arr pool[Size + 5];
long long sum[Size + 5];
int index[Size + 5];
int sz;

void init(int len, int tot = 400)
{
	for (int t = 1; t <= tot; t++)
	{
		auto a = generate(len);
		auto res = calc(a);
		if (res > Lim)
			continue;

		sz++;
		pool[sz] = a;
		sum[sz] = res;
		index[sz] = sz;
	}
	return ;
}

int ans[S + 5], cnt;
void add(arr a, int base)
{
	for (auto v: a)
		ans[++cnt] = v + base;
	return ;
}

void solve()
{
	for (int len = 2; len <= 50; len++)
		init(len);
	sort(index + 1, index + sz + 1, [&](int x, int y){ return sum[x] < sum[y]; });

	long long n;
	cin >> n;

	int base = 1, it = sz;
	while (n)
	{
		while (sum[ index[it] ] > n)
			it--;

		int p = index[it];
		n -= sum[p];
		add(pool[p], base);

		base += 2;
	}

	cout << cnt << endl;
	for (int i = 1; i <= cnt; i++)
		cout << ans[i] << " ";
	cout << endl;
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

毫无道理的正解

固定一种构造，在此基础上调整。
构造 \(p_1, \cdots, p_n, 1, \cdots, n\)，即一个排列 \({p_n}\) 接着 \(1 \to n\)。合法串的两部分一定分属前后，因此只需 \({p_n}\) 的递增子序列数为 \(n\)。
归纳构造，假设已经构造了 \(p_1, p_2, \cdots, p_k\)，当前共 \(sum\) 个合法。考虑 \(k + 1\) 的两种放法：

\[\begin{cases} k + 1, p_1, p_2, \cdots p_k \; &sum \to sum + 1 \\ p_1, p_2, \cdots, p_k, k + 1 \; &sum \to 2sum \end{cases} \]

二进制拆分，最多需要 \(2 \log_2 n = 160\) 位

代码略。

\(\Large\text{D. Colorful Balls}\)

初始序列什么样子显然没用。将可交换的关系看作边，则这张 \(n\) 个点的图分成若干个连通块，易知每个块内可以任意重排。

一个有 \(k\) 种颜色的块 \(sz = s_1 + s_2 + \cdots + s_k\) 有 \(\dfrac{sz !}{\prod s_i !}\) 种合法方案，这是经典的。总方案数即每个块的情况相乘。

现在只需求出连通块。

• 同种颜色
  判断与该颜色重量最轻的能否交换，同块的点一定可以通过它间接连通
• 异种颜色
  类似的，判断与不同色的球中，重量最轻的能否交换

并查集维护。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

constexpr int N = 2e5, P = 1e9 + 7;
constexpr int Inf = 0x3f3f3f3f;

int n, x, y;
int c[N + 5], w[N + 5];

int index[N + 5];


int fa[N + 5];

int find(int u)
{
	if (fa[u] == u)
		return u;
	return fa[u] = find(fa[u]);
}
void init_dsu()
{
	for (int i = 1; i <= n; i++)
		fa[i] = i;
	return ;
}
void link(int u, int v)
{
	fa[find(u)] = find(v);
	return ;
}


int fac[N + 5], inv[N + 5];

int ksm(int d, int u)
{
	int res = 1;
	while (u)
	{
		if (u & 1)
			res = 1ll * res * d % P;
		u >>= 1;
		d = 1ll * d * d % P;
	}
	return res;
}
void init_fac()
{
	fac[0] = 1;
	for (int i = 1; i <= n; i++)
		fac[i] = 1ll * fac[i - 1] * i % P;
	
	inv[n] = ksm(fac[n], P - 2);
	for (int i = n - 1; i >= 0; i--)
		inv[i] = 1ll * inv[i + 1] * (i + 1) % P;
	return ;
}


int cnt[N + 5];

void solve()
{
	cin >> n >> x >> y;

	w[0] = Inf;
	for (int i = 1; i <= n; i++)
	{
		cin >> c[i] >> w[i];
		if (w[ index[c[i]] ] > w[i])
			index[c[i]] = i;
	}

	init_dsu();
	for (int i = 1; i <= n; i++)
	{
		if (w[i] + w[ index[c[i]] ] <= x)
			link(i, index[c[i]]);
	}
	sort(index + 1, index + n + 1, [&](int u, int v){ return w[u] < w[v]; });
	for (int i = 1; i <= n; i++)
	{
		if (c[i] == c[ index[1] ])
		{
			if (w[i] + w[ index[2] ] <= y)
				link(i, index[2]);
		}
		else
		{
			if (w[i] + w[ index[1] ] <= y)
				link(i, index[1]);
		}
	}

	init_fac();
	for (int i = 1; i <= n; i++)
		index[i] = i;
	sort(index + 1, index + n + 1, [&](int u, int v){ return find(u) < find(v); });

	int ans = 1;
	for (int l = 1, r = 1; l <= n; l = r + 1)
	{
		r = l;
		while (r + 1 <= n && find(index[r + 1]) == find(index[l]))
			r++;

		for (int i = l; i <= r; i++)
			cnt[ c[index[i]] ]++;
		ans = 1ll * ans * fac[r - l + 1] % P;
		for (int i = l; i <= r; i++)
		{
			ans = 1ll * ans * inv[ cnt[ c[index[i]] ] ] % P;
			cnt[ c[index[i]] ] = 0;
		}
	}

	cout << ans << endl;
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{E. Camel and Oases}\)

前后缀的问题宜从序列考虑？

\(v \to \lfloor v / 2 \rfloor \to \lfloor v / 4 \rfloor \to \cdots \to 0\)，至多跳 \(18\) 次。

对于 \(v = v_0\)，\(u, u + 1\) 互达 \(\leftrightarrow x_{u + 1} - x_u \leqslant v_0\)，因此所有 \(x_{u + 1} - x_u > v_0\) 的位置将序列切分，同一段内点两两互达。

考虑 \(v \to \cdots \to 0\) 中所有数对应的序列切分情况，组成树型结构，因为祖先的断点一定也是后代的断点。这片森林中，每棵树的高度不超过 \(19\)。
问题转化为，在森林的每一层选择一个点，使得每个叶子都被覆盖。对所有的树根判断，如果第一层选它，能否实现。
可惜这个转化没法做。在树上合并信息（如果有某种做法）难以避免形如 \(2^{dep} \times 2^{dep} \times \text{balabala}\) 之类的转移复杂度，其中 \(dep\) 为子树的深度（叶向）

突破口在于从序列考虑。

计算 \(f(S), \, g(S)\) 表示只在 \(S\) 代表的层中选，能覆盖的最长前缀 / 后缀。\(S\) 从第二层开始，因此至多 \(18\) 位。\(O(19 \times n) = O(n \log V)\) 预处理后需要 \(O(18 \times 2^{18}) = O(V \log V)\) 的时间来计算。

枚举第一层选哪个，进而枚举全集的划分，判断 \(f(S), \, g(U \setminus S)\) 能否拼上。

如果第一层有多于 \(19\) 个根，则一定无解，特判掉。这一部分也只需 \(O(19 \times 2^{18}) = O(V \log V)\)

总 \(O((n + V)\log V)\)

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

constexpr int N = 2e5, Lg = 18;//at most (/= 2) 18 times
constexpr int S = 1 << Lg;

int n, m, v[Lg + 5];
int x[N + 5];

int L[Lg + 5][N + 5], R[Lg + 5][N + 5];

int f[S + 5], g[S + 5];

#define P cout << "Possible" << endl
#define NP cout << "Impossible" << endl

void solve()
{
	cin >> n >> v[0];
	for (int i = 1; i <= n; i++)
		cin >> x[i];

	m = __lg(v[0]) + 1;
	for (int i = 1; i <= m; i++)
		v[i] = v[i - 1] >> 1;

	for (int d = 0; d <= m; d++)
	{
		for (int l = 1, r = 1; l <= n; l = r + 1)
		{
			r = l;
			while (r + 1 <= n && x[r + 1] - x[r] <= v[d])
				r++;

			for (int t = l; t <= r; t++)
				L[d][t] = l, R[d][t] = r;
		}
	}

	int cnt = 0;
	for (int i = 1; i <= n; i++)
		cnt += (L[0][i] == i);
	if (cnt > Lg)
	{
		for (int i = 1; i <= n; i++)
			NP;
		return ;
	}

	int s = (1 << m) - 1;
	f[0] = 0, g[0] = n + 1;
	for (int t = 1; t <= s; t++)
	{
		g[t] = n;
		for (int lst = 1; lst <= m; lst++)
		{
			if (!((t >> (lst - 1)) & 1))
				continue;
			int prv = t ^ (1 << (lst - 1));

			if (f[prv] == n)
				f[t] = n;
			else
				f[t] = max(f[t], R[lst][f[prv] + 1]);

			if (g[prv] == 1)
				g[t] = 1;
			else
				g[t] = min(g[t], L[lst][g[prv] - 1]);
		}
	}

	for (int l = 1, r = R[0][l]; l <= n; l = r + 1)
	{
		r = R[0][l];

		int res = 0;
		for (int t = 0; t <= s && !res; t++)
		{
			if (f[t] >= l - 1 && g[s ^ t] <= r + 1)
				res = 1;
		}

		for (int i = l; i <= r; i++)
		{
			if (res)
				P;
			else
				NP;
		}
	}
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{F. Prefix Median}\)

方向是套路的。先思考判定合法，再考虑计数。

先排序。

判合法

题解区有一句话很好，当必要条件堆得足够多时，它（们）就是充要条件。

考虑取值范围。\(p_i\) 是 \(2i - 1\) 个数的中位数，即各有 \(i - 1\) 个数不大于、不小于它。因此 \(p_i\) 在 \(a\) 中的排名必须在 \([i, \, 2n - i]\) 中。

再从过程入手。每次加两个不好思考，反过来，考虑每次删去两个。如果原来的中位数是 \(p\)，此时序列是 \(a\)，则删除后 \(p'\) 要么不变，要么是 \(p\) 在 \(a\) 中的前驱或后继，即至多变化一位。
形式化地说，\(\forall i \;\, \nexists j < i\) 使得 \(p_j\) 介于 \(p_i, \, p_{i + 1}\) 之间（开区间）。

这两条已经足够了。归纳证明合法性：删两个，说明条件不变。
设当前中位数为 \(p\)，左右各有 \(x\) 个数。则目前一共出现的中位数有 \(x + 1\) 个。

\(p' = p\)：除了 \(p\)，还有 \(x + 1 - 2 = x - 1\) 个中位数。而初始左右各有 \(x\) 个，因此两侧总能各找出一个未出现的数删去。
\(p' \ne p\)：不妨设 \(p' > p\)，则要删去两个不超过 \(p\) 的数。显然其中一个可以是 \(p\) 本身，而且这样是优的。在 \(x + 1\) 个中位数中，\(p, \, p'\) 各占去一个，又有 \(p' > p\)，则 \(p\) 左侧至多有 \(x - 1\) 个，也一定能找出一个未出现的数删去。

或许会问，上述证明过程中哪里用到两个必要条件。左右各有 \(x\) 个数需要第一个来保证，而第二条确保删完之后第一条依然成立，这样归纳就能继续下去。

计数

还是删数好想。

设 \(f(i, l, r)\) 表示从后往前填数，考虑到正数第 \(i\) 个，这时在排名为 \([i, 2n - i]\) 的这些数中，有 \(l\) 种数小于 \(p_i\)、\(r\) 种数大于 \(p_i\)，并且这些数还没有被第二个必要条件排除掉。
为什么是数的种类？原序列中有相同的数，对于一串相同的 \(p\)，不妨钦定它们对应的是同一个数，以避免重复计入。

从 \(i\) 到 \(i - 1\)，第一个条件说明取值范围扩大，有两个数会分别加入 \(l, \, r\)，但只有该数值第一次出现才能计入。这通过区间内与它们相邻的数与二者是否相同来判断。如果二端均相同呢？那说明取值范围内所有数均相同，在初始化时已计入，也没有问题。
然后是 \(p\) 的移动。要么不变，要么移动。对于后一种情况，比如右移，左侧合法取值会增加一（即 \(p\) 本身），右侧至少要减少一（因为 \(p'\) 不算在内）。此时不需考虑具体如何删除，只有这两个必要条件是要考虑的。

\[\begin{aligned} f(n, 0, 0) &= 1 \\ f(i, l, r) &\to f(i - 1, \; l + \Delta l, \; r + \Delta r) \\ f(i, l, r) &\to f(i - 1, \; l + 1 + \Delta l, \; r - k + \Delta r) \; k > 0 \\ f(i, l, r) &\to f(i - 1, \; l - k + \Delta l, \; r + 1 + \Delta r) \; k > 0 \end{aligned} \]

\(ans = \sum\limits_{0 \leqslant l, r \leqslant 2n - 1} f(1, l, r)\)

总 \(O(n^4)\)，但可以前缀和优化至 \(O(n^3)\)

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

constexpr int N = 50, M = N << 1;
constexpr int P = 1e9 + 7;

int n, m;
int a[M + 5];

int f[N + 5][M + 5][M + 5];

void addto(int &x, int y)
{
	x += y;
	if (x > P)
		x -= P;
	return ;
}

void solve()
{
	cin >> n;
	m = n + n - 1;
	for (int i = 1; i <= m; i++)
		cin >> a[i];
	sort(a + 1, a + m + 1);

	f[n][0][0] = 1;
	for (int t = n; t > 1; t--)
	{
		int dl = (a[t] != a[t - 1]);
		int dr = (a[n + n - t] != a[n + n - t + 1]);
		
		for (int l = 0; l <= m; l++)//actually, is 2(n - t + 1) - 1, which is the length of the interval
		for (int r = 0; r <= m; r++)
		{
			int L = l + dl, R = r + dr;
			addto(f[t - 1][L][R], f[t][l][r]);

			for (int k = 1; k <= L; k++)//at least 1, because the new median is no longer belongs to the left
				addto(f[t - 1][L - k][R + 1], f[t][l][r]);//cur median is still useful, so + 1
			for (int k = 1; k <= R; k++)
				addto(f[t - 1][L + 1][R - k], f[t][l][r]);
		}

		/* O(n^3) version
		for (int R = m; R >= dr + 1; R--)
		for (int L = m, sum = 0; L >= max(0, dl - 1); L--)
		{
			addto(sum, f[t][L - dl + 1][R - dr - 1]);
			addto(f[t - 1][L][R], sum);
		}

		for (int L = m; L >= dl + 1; L--)
		for (int R = m, sum = 0; R >= max(0, dr - 1); R--)
		{
			addto(sum, f[t][L - dl - 1][R - dr + 1]);
			addto(f[t - 1][L][R], sum);
		}
		*/
	}

	int ans = 0;
	for (int l = 0; l <= m; l++)
	for (int r = 0; r <= m; r++)
		addto(ans, f[1][l][r]);
	cout << ans << endl;
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\[\Huge\mathrm{AGC \; 013} \]

---

\(\Large\text{A. Sorted Arrays}\)

是子段不是子序列，贪心即可。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

const int N = 1e5;

int n;
int a[N + 5];

void solve()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
		cin >> a[i];

	int ans = 0;
	for (int l = 1, r = 1; l <= n; l = r + 1)
	{
		ans++;

		r = l;
		while (r + 1 <= n && a[r + 1] == a[l])
			r++;

		l = r;
		while (r + 1 <= n && 
				(a[r + 1] == a[r] || (a[l] < a[l + 1]) == (a[r] < a[r + 1])))
			r++;
	}
	cout << ans << endl;
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{B. Hamiltonish Path}\)

想不出来的 \(\mathrm{Adhoc}\) 题

直接做。以任意两个相邻的点 \(\{ s, t\}\) 开始，考虑如下过程：

记当前考虑的点为 \(u\)。

若 \(u\) 的邻域均在序列中，停止。

否则，从邻域中任取一个不在序列中的点 \(v\)，令 \(u \gets v\)。

对 \(s, t\) 各做一次，最终的序列即为所求。

证明：首先必停机，因为每次取出的点互不同。其次，合法性可以反证。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

const int N = 1e5;

int n, m;
vector<int> e[N + 5];

int in[N + 5];
deque<int> ans;

void solve()
{
	cin >> n >> m;
	for (int i = 1, u, v; i <= m; i++)
	{
		cin >> u >> v;
		e[u].push_back(v);
		e[v].push_back(u);
	}

	auto check = [&](int u)
	{
		for (auto v: e[u])
		{
			if (!in[v])
				return v;
		}
		return 0;
	};

	in[1] = 1;
	ans.push_back(1);
	
	while (1)
	{
		int u = ans.back();
		int v = check(u);
		if (!v)
			break;

		in[v] = 1;
		ans.push_back(v);
	}

	while (1)
	{
		int u = ans.front();
		int v = check(u);
		if (!v)
			break;

		in[v] = 1;
		ans.push_front(v);
	}

	cout << ans.size() << endl;
	for (auto u: ans)
		cout << u << " ";
	cout << endl;
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
} 

\(\Large\text{C. Ants on a Circle}\)

思路经典，但是细节非常多……

抛开对应关系不谈，只求最后位置是容易的：只需认为蚂蚁相互穿过而非掉头。而编号永远连续，问题归结为如何找到第一只蚂蚁的位置（或在第一只蚂蚁位置上的实际是谁）。

不妨第一只顺时针走。考虑第一次碰面，“第一只”正常前进，不过编号变为 2。因此，每碰面一次，“第一只”的编号加一，而碰面是可以逐只累加的。

有一个细节：最终位置重合。这确实是可能的，比如两只蚂蚁相向而行，时间恰当。此时必须要区分二者，否则考虑如下例子：

x[]: 1, 2, 2, 3, 4
ans1: 2, 3, 4, 1, 2
ans2: 2, 2, 3, 4, 1

之前为了碰头计算方便，把重合的情况算入了。因此，重合也应认为彼此交错。比如顺时针走，则应选择按顺时针排布后更靠后的那只。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

const int N = 1e5;

int n, L, T;
int x[N + 5], w[N + 5];

void solve()
{
	cin >> n >> L >> T;
	for (int i = 0; i < n; i++)
		cin >> x[i] >> w[i];

	int cnt = 0;//how many times 0-th meet with others
	for (int i = 1; i < n; i++)
	{
		if (w[0] == w[i])
			continue;

		auto calc = [&](int d) -> int
		{
			double t = T - d / 2.0;//first meet is special
			if (t < 0)
				return 0;

			int res = 1;
			res += t / (L / 2.0);
			return res;
		};

		int dist = x[i] - x[0];
		if (w[0] == 1)
			cnt = (cnt + calc(dist)) % n;
		else
			cnt = (cnt + calc(L - dist)) % n;
	}

	for (int i = 0; i < n; i++)
		x[i] = (x[i] + (w[i] == 1 ? T : -T) % L + L) % L;

	int mark = x[0];
	sort(x, x + n);

	int base = 0;
	while (x[base] != mark)
		base++;
	if (base + 1 < n && x[base] == x[base + 1] && w[0] == 1)
		base++;
	/*
		find where is 0-th now
		the only problem is, two ants may at the same position in the end
		according to calc, we actually assume that two ants have crossed each other, which is easier to code
		-> <-  =>  <- ->
		so if 0-th is clockwise, the right one is 0-th
		otherwise, choose the left
	*/

	int s = (base + n + (w[0] == 1 ? -cnt : cnt)) % n;
	for (int i = 1; i <= n; i++, s = (s + 1) % n)
		cout << x[s] << "\n";
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{D. Piling Up}\)

简化过程。不妨认为第二次取球时，取走上一步放入的。因此，每回合形如：先取走一个，再放入一个。对取 + 放构成的序列计数。

球的总数不变。容易想到这样的状态：前 \(i\) 轮后，红球剩 \(r\) 个，蓝球剩 \(b = n - r\) 个，共 \(dp_{i, r}\) 种。但有重复计数的情况。比如两种球都富裕不少，初始数量增减不影响序列生成。

因此，需要加限定条件：\(r\) 为保证能生成的最小红球数。当然红球未必是瓶颈，限制由蓝球完成，或先后多次交错成为瓶颈。修改为 \(dp_{i, r, 0/1, 0/1}\)：前 \(i\) 轮后，现在有 \(r\) 个红球，红 / 蓝球是否成为过瓶颈。

从折线图考虑更清晰。把 \((i, r)\) 画在坐标系上，则每一种折线的形状均对应一种序列。只关心形状，起点、终点任意。总可以平移折线，使其上端或下端接触边界 \(y = n\) 或 \(y = 0\)。成为瓶颈即触线。

如何统计答案？只统计触线。对于只触一侧的折线，在上或下统计是一样的。还有上下均触。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

constexpr int N = 3000, P = 1e9 + 7;

int n, m;
int dp[N + 5][N + 5][2][2];
/*
	each round is regarded as: take one, then add one
	
	dp[i][r][x][y]: x for red, y for blue
	after i rounds, r red balls, b = n - r blue balls in the box
	whether exist a time between [1, i], where no red / blue balls remain

	only count how many patterns
	(x, y): (1, 0) = (0, 1), while (1, 1) is different from both, and both include (0, 0)
*/

void solve()
{
	cin >> n >> m;

	auto add = [](int &x, int y)
	{
		x += y;
		if (x > P)
			x -= P;
		if (x > P)//because of w + w, 2nd formula
			x -= P;
		return ;
	};

	for (int r = 0; r <= n; r++)
		dp[0][r][0][0] = 1;
	
	for (int i = 0; i < m; i++)
	{
		for (int r = 0, b = n; r <= n; r++, b--)
		for (int x = 0; x < 2; x++)
		for (int y = 0; y < 2; y++)
		{
			int w = dp[i][r][x][y];
			
			// r, r
			if (r >= 1)
				add(dp[i + 1][r][x | (r == 1)][y | (b == 0)], w);

			// r, b
			if (r >= 1)
				add(dp[i + 1][r - 1][x | (r == 1)][y | (b == 0)], w);

			// b, r
			if (b >= 1)
				add(dp[i + 1][r + 1][x | (r == 0)][y | (b == 1)], w);

			// b, b
			if (b >= 1)
				add(dp[i + 1][r][x | (r == 0)][y | (b == 1)], w);
		}
	}

	int ans = 0;
	for (int r = 0; r <= n; r++)
	{
		add(ans, dp[m][r][1][0]);
		add(ans, dp[m][r][1][1]);
	}
	cout << ans << '\n';
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{E. Placing Squares}\)

数据范围上，指示了矩阵加速。不过仍然看了题解……拆解方式值得记录。

从简单 \(dp\) 入手，设 \(dp_i\) 表示前 \(i\) 格所有方式的答案。有：

\[dp_i = \begin{cases} \sum\limits_{0 \leqslant j < i} dp_j \times (i - j)^2, & \text{if } i \not= x_k, \forall k \\ 0, & \text{if } i = x_k \end{cases} \]

其中初始 \(dp_0 = 1\)。

先考虑一般情况。涉及到二次项，维护

\[\begin{aligned} a &= \sum\limits_{0 \leqslant j < i} dp_j \times (i - j)^2 \\ b &= \sum\limits_{0 \leqslant j < i} dp_j \times (i - j) \\ c &= \sum\limits_{0 \leqslant j < i} dp_j \end{aligned} \]

注意到 \(dp_i = a\)。从 \(i \; \to \; i + 1\)（这样非法情况恰好在 \(i = x_k\) 处考虑）：

\[\begin{aligned} a' &= \sum\limits_{j = 0}^{i} dp_j \times (i + 1 - j)^2 \\ &= dp_i + \sum\limits_{j = 0}^{i - 1} dp_j \times \left( (i - j)^2 + 2(i - j) + 1 \right) \\ &= dp_i + a + 2b + c \end{aligned} \]

同理可得：

\[\begin{aligned} b' &= dp_i + b + c \\ c' &= dp_i + c \end{aligned} \]

因此有：

\[\begin{vmatrix} a' \\ b' \\ c' \end{vmatrix} = \begin{vmatrix} 2 \; &2 \; &1 \\ 1 \; &1 \; &1 \\ 1 \; &0 \; &1 \end{vmatrix} \times \begin{vmatrix} a \\ b \\ c \end{vmatrix} \text{（一般）} \quad\quad \begin{vmatrix} a' \\ b' \\ c' \end{vmatrix} = \begin{vmatrix} 1 \; &2 \; &1 \\ 0 \; &1 \; &1 \\ 0 \; &0 \; &1 \end{vmatrix} \times \begin{vmatrix} a \\ b \\ c \end{vmatrix} \text{（特殊）} \]

有零星的细节，比如最后哪里是答案。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

constexpr int N = 1e5, P = 1e9 + 7;

int n, m;
int a[N + 5];

void add(long long &x, long long y)
{
	x = (x + y) % P;
	return ;
}

struct Matrix
{
	long long v[3][3];

	Matrix(int type = 0)
	{
		for (int i = 0; i < 3; i++)
			for (int j = 0; j < 3; j++)
				v[i][j] = 0;

		if (type == 1)//I
			v[0][0] = v[1][1] = v[2][2] = 1;
		if (type == 2)//normal
		{
			v[0][0] = 2, v[0][1] = 2, v[0][2] = 1;
			v[1][0] = 1, v[1][1] = 1, v[1][2] = 1;
			v[2][0] = 1, v[2][1] = 0, v[2][2] = 1;
		}
		if (type == 3)//abnormal
		{
			v[0][0] = 1, v[0][1] = 2, v[0][2] = 1;
			v[1][0] = 0, v[1][1] = 1, v[1][2] = 1;
			v[2][0] = 0, v[2][1] = 0, v[2][2] = 1;
		}
		return ;
	}
};
Matrix A(2), B(3);

Matrix operator * (Matrix x, Matrix y)
{
	Matrix z;
	for (int i = 0; i < 3; i++)
		for (int j = 0; j < 3; j++)
			for (int k = 0; k < 3; k++)
				add(z.v[i][j], x.v[i][k] * y.v[k][j]);
	return z;
}
Matrix pow(Matrix x, int u)
{
	Matrix res(1);
	while (u)
	{
		if (u & 1)
			res = res * x;
		x = x * x;
		u >>= 1;
	}
	return res;
}

/*
	f(n) = sum_(0 <= t < n) f(t) * (n - t)^2
	or f(n) = 0, if n = a[i]

	a = sum_(0 <= t < n) f(t) * (n - t)^2
	b = sum_(0 <= t < n) f(t) * (n - t)
	c = sum_(0 <= t < n) f(t)

	n -> n + 1
	a' = f(n) + a + 2b + c
	b' = f(n) + b + c
	c' = f(n) + c

	normal:
	| a' |   | 2 2 1 |   | a |
	| b' | = | 1 1 1 | * | b |
	| c' |   | 1 0 1 |   | c |

	abnormal:
	| a' |   | 1 2 1 |   | a |
	| b' | = | 0 1 1 | * | b |
	| c' |   | 0 0 1 |   | c |

	a[i] = x: between x-th and (x+1)-th
	a: not consider n = a[i], what will f(n) be
	
	begin: a = b = c = 1, at n = 1
	end: n - 1 matrices, not n
*/

void solve()
{
	cin >> n >> m;
	for (int i = 1; i <= m; i++)
		cin >> a[i];
	a[0] = 0;

	Matrix mat(1);
	for (int i = 1; i <= m; i++)
	{
		mat = pow(A, a[i] - a[i - 1] - 1) * mat;
		mat = B * mat;
	}
	mat = pow(A, n - a[m] - 1) * mat;

	cout << (mat.v[0][0] + mat.v[0][1] + mat.v[0][2]) % P << '\n';
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{F. Two Faced Cards}\)

第一个独立切的模拟费！！！111

题意即最小化翻牌次数。首先将 \(c\) 从小到大排序，则一个数能匹配 \(c\) 的一段后缀。下文 \(a, b, d, e\) 均指离散化后，在 \(c\) 中能匹配的最早位置，其中 \(c\) 为 \(0-\mathrm{index}\)。

看着很模拟费用流，于是从此入手。考虑如下模型：

• 建超级源 \(S\) 、汇 \(T\)
• 对每张牌 \((a, b)\)，设虚点 \(u\) 代表之。连边：
  • \(S \to u\)，流量 \(1\)，费用 \(0\)。
  • \(u \to a\)，流量 \(\infty\)，费用 \(0\)。
  • \(u \to b\)，流量 \(\infty\) ，费用 \(1\)，代表翻牌。
• 对于 \(c\)，连一条链 \(0 \to 1 \to \cdots \to n\)，下文称为“主链”。每个点 \(i\) 连边 \(i \to T\)。主链和分叉上所有边流量 \(\infty\)，费用 \(0\)。

求最小费用最大流。有解当且仅当 \(\mathrm{flow} = n + 1\)。

由于每次只加入一张牌，考虑处理出只有 \(n\) 张牌时的残量网络。新加入一张牌，\(\mathrm{flow}\) 至多加一，故有解的必要条件是初始 \(\mathrm{flow} = n\)，也即每张牌都能匹配。

显然不能暴力增广。现在允许放弃一个 \(c\)，自然放弃 \(c_0\) 是最优的，问题归为 \(n\) 张牌如何完美匹配 \(c_1 \sim c_n\)。

假设选定最终牌上的数字。记 \(cnt_i\) 为 \(c_i\) 能匹配的牌数，则必有 \(\forall i \in \{1, \cdots, n\}, \;\; cnt_i \geqslant i\)，这是经典的。

考虑贪心，所有牌都选正面。用差分记录 \(cnt_i - i\)。从前往后扫，直到第一个 \(cnt_i - i < 0\) 的位置，由第一知此时 \(cnt_i - i = -1\)。只需翻动一张牌 \((a, b)\)，使 \(1 \sim i\) 中多一个供给，\(i\) 处得以匹配，因而要求 \(b \leqslant i < a\)。如有多种候选，如何抉择？选出的牌对 \(i\) 之后毫无用处（用来填线），而 \(a\) 越大，潜在的贡献越小（因只作用于 \(a\) 之后），损失也越小。所以选 \(a\) 最大的那一张，可用 \(1\log\) 维护。

上述过程如无法进行到底，则必无解。否则，确定了每张牌的翻动情况，再推一遍差分即得主链各边流量。

考察残量网络的形态，有流量的边无非：始终存在的 \(i \to i + 1\)；正向有流产生的 \(i - 1 \gets i\)；翻动或反悔的 \(a \to u \to b\) 与 \(b \to u \to a\)。依然由贪心，翻牌只翻 \(a > b\)，反悔只反 \(b < a\)。新增一张牌，最多带来一条增广路，故流量本质只分 \(0 / 1\)。所以，最后一类可视为主链上新增 \(u \to v\)，向前表翻动，费用 \(1\)；向后表反悔，费用 \(-1\)。

不妨枚举新牌选哪面，则变为寻找从定点到 \(0\) 的最短路（这是费用流）。又是经典操作：建反图，以 \(0\) 为起点预处理所有最小距离。

或许你已经准备扔一个 dijkstra 上去了。且慢，图有负权边！具体地，边权为 \(0, \pm 1\)。这里采用 SPFA，跑得飞快。复杂度自然难说，但估计很难卡掉——毕竟不是网格图。

结束了……吗？最短路的正确性源于何？既有负权边，为何无负环？并非数据水。反证，如果增广路上有负环，则环中 \(-1\) 边比 \(1\) 边多，即反变正的牌多于正变反的牌。按此操作，只考虑初始 \(n\) 张牌，那么代价降低了。但从匹配考虑，原先 \(c_0\) 失配，现在新牌匹配某个 \(c_i\)，\(c_0\) 由初始纸牌负责，代价必然不减。贪心决定了初始代价的最小性，继而引出矛盾。

代码很短很好写，稍加注意一些无解和临界的判断。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>
#include <queue>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

constexpr int N = 1e5 + 1;
typedef pair<int, int> pir;

int n, q;
int card[N + 5][2];//front, back
int c[N + 5];

void failed()
{
	cin >> q;
	while (q--)
		cout << "-1\n";
	exit(0);
}

int cost;
int flip[N + 5];

int flow[N + 5];
vector<int> box[N + 5];

void match()
{
	for (int i = 1, fr, bk; i <= n; i++)
	{
		fr = card[i][0], bk = card[i][1];
		
		if (fr > n)
		{
			if (bk > n)
				failed();

			cost++, flip[i] = 1;
			flow[bk]++;
			continue;
		}

		flow[fr]++;
		if (bk < fr)
			box[bk].push_back(i);
	}

	set<pir> s;//{fr, id}
	for (auto v : box[0])
		s.insert(pir{-card[v][0], v});

	for (int i = 1; i <= n; i++)
	{
		flow[i] += flow[i - 1] - 1;
		for (auto v : box[i])
			s.insert(pir{-card[v][0], v});

		if (flow[i] < 0)//equal to -1
		{
			if (s.empty())
				failed();

			int u = s.begin() -> second;
			s.erase(s.begin());

			if (card[u][0] <= i)
				failed();

			cost++, flip[u] = 1;
			flow[card[u][0]]--, flow[i]++;
		}
	}

	for (int i = 0; i <= n; i++)
		flow[i] = 0;
	for (int i = 1; i <= n; i++)
		flow[ card[i][flip[i]] ]++;

	for (int i = 1; i <= n; i++)
		flow[i] += flow[i - 1] - 1;
	return ;
}

vector<int> edge[N + 5];
int dis[N + 5], in[N + 5];

void init()
{
	for (int i = 1; i <= n; i++)
	{
		dis[i] = N + 1;

		int fr = card[i][0], bk = card[i][1];
		if (fr > n || bk > n || fr <= bk)
			continue;

		if (flip[i])
			edge[fr].push_back(bk);
		else
			edge[bk].push_back(fr);
	}

	queue<int> que;
	que.push(0), in[0] = 1;

	while (!que.empty())
	{
		int u = que.front();
		que.pop(), in[u] = 0;

		auto relaxation = [&](int v, int w) -> void
		{
			if (dis[v] <= w)
				return ;

			dis[v] = w;
			if (!in[v])
				que.push(v);
			return ;
		};

		if (u + 1 <= n && flow[u] > 0)
			relaxation(u + 1, dis[u]);
		if (u >= 1)
			relaxation(u - 1, dis[u]);
		for (auto v : edge[u])
			relaxation(v, dis[u] + (v < u ? -1 : 1));
	}
	return ;
}

void solve()
{
	cin >> n;

	for (int i = 1; i <= n; i++)
		cin >> card[i][0] >> card[i][1];
	for (int i = 0; i <= n; i++)
		cin >> c[i];

	sort(c, c + n + 1);
	for (int i = 1; i <= n; i++)
	{
		card[i][0] = lower_bound(c, c + n + 1, card[i][0]) - c;
		card[i][1] = lower_bound(c, c + n + 1, card[i][1]) - c;
	}

	match();
	init();

	cin >> q;
	for (int i = 1, d, e, wd, we; i <= q; i++)
	{
		cin >> d >> e;
		d = lower_bound(c, c + n + 1, d) - c;
		e = lower_bound(c, c + n + 1, e) - c;

		auto calc = [&](int u, int f) -> int
		{
			if (u > n || dis[u] > N)
				return -1;
			return cost + dis[u] + f;
		};

		wd = calc(d, 0), we = calc(e, 1);
		if (wd == -1 && we == -1)
			cout << "-1\n";
		else if (wd == -1 || we == -1)
			cout << n + 1 - (wd == -1 ? we : wd) << '\n';
		else
			cout << n + 1 - min(wd, we) << '\n';
	}
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\[\Huge\mathrm{AGC \; 014} \]

---

\(\Large\text{A. Cookie Exchanges}\)

暴力，直觉上就是对的。证明不难。

设当前三个数为 \(2x \leqslant 2y \leqslant 2z \; (x, y, z \in \mathrm{N}_+)\)，则操作后为 \(x + y \leqslant x + z \leqslant y + z\)。

需要一个每次减少的量，极差正好：\(2(z - x) \to (z - x)\)，因此至多 \(\log V\) 次。

细节：极差为 0 要特判。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

void solve()
{
	int a[3];
	for (int i = 0; i < 3; i++)
		cin >> a[i];

	sort(a, a + 3);
	int cnt = 0;

	while (a[0] < a[2])
	{
		for (int i = 0; i < 3; i++)
		{
			if (a[i] & 1)
				return cout << cnt << '\n', void();
			a[i] /= 2;
		}

		int b[3] = {};
		for (int i = 0; i < 3; i++)
			b[i] = a[(i + 1) % 3] + a[(i + 2) % 3];
		sort(b, b + 3);

		for (int i = 0; i < 3; i++)
			a[i] = b[i];
		cnt++;
	}

	cout << (a[0] & 1 ? cnt : -1) << '\n';
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{B. Unplanned Queries}\)

大胆猜。

从简单的必要条件入手。最终每条边覆盖偶数次，则每个点的度数也皆偶。

只需说明该条件充分，给构造即可。考虑归纳，每次尝试删一个点。任取 \(v\) 作为叶子，再任取 \(u\) 作为父亲，则 \(u\) 会继承 \(v\) 的点对。由于 \(v\) 只有一条边，覆盖次数必为偶数。分讨 \(u\)，显然本质上只有 \((u, v)\) 存在与否两种情况。

• 不存在：\(u\) 新增偶数个点对。
• 存在：刨除 \((u, v)\)，\(u\) 必有另外奇数个点对，\(v\) 同理。合并后，\(u\) 仍有偶数个点对。

事实上，随便一棵树都是对的。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

constexpr int N = 1e5;

int n, m;
int deg[N + 5];

void solve()
{
	cin >> n >> m;
	for (int i = 1, u, v; i <= m; i++)
	{
		cin >> u >> v;
		deg[u]++, deg[v]++;
	}

	for (int i = 1; i <= n; i++)
	{
		if (deg[i] & 1)
			return cout << "NO\n", void();
	}
	cout << "YES\n";
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{C. Closed Rooms}\)

普及题……

把第一步单独拿出来，之后每回合均为先解锁再行走，因此可以随便走。看第一步能到哪里，直行到墙。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

constexpr int N = 800;

int n, m, k;
int x, y;
char c[N + 5][N + 5];

int calc(int i, int j)
{
	auto need = [](int dis)
	{
		return (dis + k - 1) / k;
	};

	return min({need(i - 1), need(j - 1), need(n - i), need(m - j)});
}

int dep[N + 5][N + 5];
constexpr int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};

void solve()
{
	cin >> n >> m >> k;
	for (int i = 1; i <= n; i++)
	for (int j = 1; j <= m; j++)
	{
		cin >> c[i][j];
		if (c[i][j] == 'S')
			x = i, y = j;
	}

	queue<int> q;
	auto id = [](int i, int j)
	{
		return i * 1000 + j;
	};

	dep[x][y] = k + 1;
	q.push(id(x, y));

	int ans = n * m;
	while (!q.empty())
	{
		int u = q.front();
		q.pop();

		int i = u / 1000, j = u % 1000;
		ans = min(ans, 1 + calc(i, j));

		if (dep[i][j] == 1)
			continue;

		for (int t = 0; t < 4; t++)
		{
			int xx = i + dx[t], yy = j + dy[t];
			if (xx <= 0 || xx > n || yy <= 0 || yy > m)
				continue;
			if (c[xx][yy] != '.' || dep[xx][yy])
				continue;

			dep[xx][yy] = dep[i][j] - 1;
			q.push(id(xx, yy));
		}
	}

	cout << ans << '\n';
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{D. Black and White Tree}\)

极其困难的，看了题解。（却不是本场最困难的 [惊恐.jpg]

考虑叶子节点。先手将其父亲染白，逼迫后手染黑叶子。如果叶子已经被染白，则后手也必须染黑其父亲。这样暗示了一种自底向上每次删两个点的做法。没有实现该思路。

进一步地，上述过程与求树的完美匹配相同。若存在完美匹配，则后手只需染黑前一步的匹配点，后手必胜。若不存在，则存在一些孤立点。感性理解，先手抢占孤立点（？）（比如，两个叶子的菊花图），使得后手无计可施。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

constexpr int N = 1e5;

int n;
vector<int> e[N + 5];

int match[N + 5];
void dfs(int u, int fa)
{
	int cnt = 0;
	for (auto v : e[u])
	{
		if (v == fa)
			continue;

		dfs(v, u);
		cnt += !match[v];
	}

	if (cnt == 0)
		return ;
	if (cnt > 1)
		cout << "First\n", exit(0);
	match[u] = 1;
	return ;
}

void solve()
{
	cin >> n;
	for (int i = 1, u, v; i < n; i++)
	{
		cin >> u >> v;
		e[u].push_back(v);
		e[v].push_back(u);
	}

	dfs(1, 0);
	cout << (match[1] ? "Second" : "First") << '\n';
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{E. Blue and Red Tree}\)

国人数据结构训魔怔了，基本都正面想想然后启动 ds。比如我。

考虑第一条红边 \(<u, v>\)。移除 \(u \sim v\) 路径上一条蓝边，树分裂为两个连通块，之后的操作不能跨越二者。因此必须选择恰被 \(u \sim v\) 覆盖一次的蓝边。

做法已经呼之欲出了！维护边覆盖次数，每次取只覆盖一次的边，找到对应的路径，删去该路径。树剖即可。找路径可以通过线段树每个点再开一个 set 实现，时间飙升至 \(O(n \log^3 n)\)，也能过。聪明实现是维护路径编号 \(\text{xor}\) 和。

点击查看 DS 代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
#include <set>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

constexpr int N = 1e5;

int n;
vector<int> e[N + 5];

int path[N + 5][2];

int dep[N + 5], fa[N + 5], sz[N + 5], son[N + 5];
int dfn[N + 5], tim;
int top[N + 5];

void dfs1(int u, int fr)
{
	dep[u] = dep[fr] + 1;
	fa[u] = fr;
	sz[u] = 1;

	int tmp = 0;
	for (auto v : e[u])
	{
		if (v == fr)
			continue;

		dfs1(v, u);
		sz[u] += sz[v];
		if (!tmp || sz[v] > sz[tmp])
			tmp = v;
	}
	son[u] = tmp;
	return ;
}
void dfs2(int u, int fr, int tp)
{
	dfn[u] = ++tim;
	top[u] = tp;

	if (son[u])
		dfs2(son[u], u, tp);

	for (auto v : e[u])
	{
		if (v == fr || v == son[u])
			continue;
		dfs2(v, u, v);
	}
	return ;
}

namespace Tree
{
	constexpr int SZ = N << 2;

	struct Node
	{
		int key, id;//range min
		set<int> path;
		int tag;
	};
	Node node[SZ + 5];

	#define ls(p) (p << 1)
	#define rs(p) (p << 1 | 1)

	#define key(p) node[p].key
	#define id(p) node[p].id
	#define tag(p) node[p].tag

	void pushup(int p)
	{
		key(p) = min(key(ls(p)), key(rs(p)));
		id(p) = (key(p) == key(ls(p)) ? id(ls(p)) : id(rs(p)));
		return ;
	}
	void add(int p, int v)
	{
		key(p) += v;
		tag(p) += v;
		return ;
	}
	void pushdown(int p)
	{
		add(ls(p), tag(p));
		add(rs(p), tag(p));
		tag(p) = 0;
		return ;
	}

	void build(int p, int l, int r)
	{
		id(p) = l;
		if (l == r)
			return ;

		int mid = (l + r) >> 1;
		build(ls(p), l, mid);
		build(rs(p), mid + 1, r);
		return ;
	}

	void modify(int p, int l, int r, int L, int R, int pid, int v)
	{
		if (L <= l && r <= R)
		{
			add(p, v);
			if (v == 1)
				node[p].path.insert(pid);
			else
				node[p].path.erase(pid);
			return ;
		}

		int mid = (l + r) >> 1;
		pushdown(p);

		if (L <= mid)
			modify(ls(p), l, mid, L, R, pid, v);
		if (R > mid)
			modify(rs(p), mid + 1, r, L, R, pid, v);
		pushup(p);
		return ;
	}
	int find(int index)
	{
		int p = 1, l = 1, r = n;
		while (node[p].path.empty())
		{
			int mid = (l + r) >> 1;

			if (index <= mid)
			{
				p = ls(p);
				r = mid;
			}
			else
			{
				p = rs(p);
				l = mid + 1;
			}
		}
		return *node[p].path.begin();
	}

	void adjust(int p, int l, int r)
	{
		if (key(p) > 0)
			return ;
		if (l == r)
			return key(p) = N + 1, void();

		int mid = (l + r) >> 1;
		pushdown(p);

		adjust(ls(p), l, mid);
		adjust(rs(p), mid + 1, r);
		pushup(p);
		return ;
	}
	void adjust()
	{
		while (key(1) == 0)
			adjust(1, 1, n);
		return ;
	}
}

void modify(int pid, int val)
{
	int u = path[pid][0], v = path[pid][1];

	while (top[u] != top[v])
	{
		if (dep[top[u]] < dep[top[v]])
			swap(u, v);

		int w = top[u];
		Tree :: modify(1, 1, n, dfn[w], dfn[u], pid, val);

		u = fa[w];
	}

	if (dep[u] < dep[v])
		swap(u, v);
	if (u != v)
		Tree :: modify(1, 1, n, dfn[v] + 1, dfn[u], pid, val);
	return ;
}

void solve()
{
	cin >> n;
	for (int i = 1, u, v; i < n; i++)
	{
		cin >> u >> v;
		e[u].push_back(v);
		e[v].push_back(u);
	}
	for (int i = 1; i < n; i++)
		cin >> path[i][0] >> path[i][1];

	dfs1(1, 0);
	dfs2(1, 0, 1);
	
	Tree :: build(1, 1, n);
	for (int i = 1; i < n; i++)
		modify(i, 1);
	Tree :: adjust();

	for (int r = 1; r < n; r++)
	{	
		if (Tree :: node[1].key != 1)
			return cout << "NO\n", void();

		int pid = Tree :: node[1].id;
		pid = Tree :: find(pid);

		modify(pid, -1);
		Tree :: adjust();
	}
	cout << "YES\n";
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

存在简单做法，即官方题解。

上述为正向思考，不妨从反面试试。最后一条红边必然与蓝边重合，可以缩合两个点。对每个点存蓝边和红边，每次取重合的边，合并两个点及集合。能缩至一个单点即有解，复杂度 \(O(n \log^2 n)\)。

点击查看启发式合并代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <set>
#include <queue>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

constexpr int N = 1e5;

int n;
set<int> blue[N + 5], red[N + 5];

int fa[N + 5];
int find(int x)
{
	if (fa[x] == x)
		return x;
	return fa[x] = find(fa[x]);
}

queue<long long> q;

void solve()
{
	cin >> n;
	for (int i = 1, u, v; i < n; i++)
	{
		cin >> u >> v;
		blue[u].insert(v);
		blue[v].insert(u);
	}
	for (int i = 1, u, v; i < n; i++)
	{
		cin >> u >> v;
		red[u].insert(v);
		red[v].insert(u);
	}

	for (int i = 1; i <= n; i++)
		fa[i] = i;
	auto calc = [](int u, int v){ return ((1ll * u) << 17) | v; };
	
	for (int u = 1; u <= n; u++)
	{
		for (auto v : blue[u])
		{
			if (red[u].find(v) != red[u].end())
				q.push(calc(u, v));
		}
	}

	int cnt = 0;
	while (!q.empty())
	{
		int u = q.front() >> 17, v = q.front() & 131071;
		q.pop();

		u = find(u), v = find(v);
		if (u == v)
			continue;
		cnt++;

		if (blue[u].size() + red[u].size() > blue[v].size() + red[v].size())
			swap(u, v);

		fa[u] = v;
		blue[u].erase(v);
		blue[v].erase(u);
		red[u].erase(v);
		red[v].erase(u);

		set<int> tmp;
		for (auto w : blue[u])
		{
			blue[w].erase(u);
			blue[w].insert(v);
			blue[v].insert(w);
			tmp.insert(w);
		}
		for (auto w : red[u])
		{
			red[w].erase(u);
			red[w].insert(v);
			red[v].insert(w);
			tmp.insert(w);
		}

		for (auto w : tmp)
		{
			if (blue[v].find(w) != blue[v].end() && red[v].find(w) != red[v].end())
				q.push(calc(v, w));
		}
	}

	cout << (cnt == n - 1 ? "YES" : "NO") << '\n';
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}

\(\Large\text{F. Strange Sorting}\)

这是人类能做出的东西吗……？本场真正的大 \(\mathrm{Boss}\)。

先注意到，1 不会影响其它元素是 high / low，也不会影响操作后它们的相对位置。这启示通过删去 1 来入手，或者进一步地，按 \(n \to 1\) 逐个加入，递推答案。

假设删去 1，\(2 \sim n\) 需要 \(t\) 步排序。

• \(t = 0\)：原序列即顺序。

  若 1 位于开头，\(ans = 0\)；反之若 1 不在开头，\(ans = 1\)。

• \(t > 0\)

  同上，1 在开头则 \(ans = t\)，否则 \(ans = t + 1\)。

问题归结为如何判断 1 是否在开头。

考虑 \(t - 1\) 步时的序列（这正是需要特判 0 的原因），有如下结论：

• 2 必不在开头。

  反证：若在且未排好序，则下一步有 low 元素排在 2 之前，矛盾。

设此时以 \(f\) 开头，由上知 \(f > 2\)。如果此时 1 位于 \(f, 2\) 之间，则下一步 1 回到开头。否则还需两步。为判断 \(f, 1, 2\) 的相对位置，需如下结论：

• 任意操作后，\((f, 1, 2)\) 的循环顺序保持不变。循环顺序指 \((a, b, c) = (b, c, a) = (c, a, b)\)。

  证明：先证明引理：

  • 只考虑 \(2 \sim n\)，在前 \(t - 1\) 步中，\(f\) 除非在第一个位置，否则永远不会成为 high 元素。

    反证：若 \(f\) 成为不在开头的 high 元素，设 \(f\) 往前一个 high 元素为 \(g\)，则操作后二者相邻。易知 \(g < f\)。此后，要么同时成为 high / low 元素，\(g\) 依然在 \(f\) 前一个；要么 \(g\) 为 low 而 \(f\) 为 high，\(g\) 之前必存在 high 元素，\(f\) 仍不会移到开头。

  对所有顺序及合法的 high / low 情况讨论，可以完成证明。

综上，只需看最初 \(f, 1, 2\) 的顺序即可。

实现上，记录 \(t_i, f_i\) 表示仅考虑 \(i \sim n\) 时的值，定义同上。当 \(t_i = 0\) 时 \(f_i\) 未定义，初始 \(t_n = 0\)。\(f\) 的递推也容易得出。总 \(O(n)\)，很厉害！

另：存在 ds 做法，暂时不会。

点击查看代码

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

// #define Debug
// #define LOCAL
// #define TestCases

constexpr int N = 2e5;

int n;
int p[N + 5], q[N + 5];

int t[N + 5], f[N + 5];

void solve()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> p[i];
		q[p[i]] = i;
	}

	auto check = [&](int x, int y, int z)
	{
		int tmp[] = {q[x], q[y], q[z]};
		for (int i = 0, j = 1, k = 2; i < 3; i++, j = (j + 1) % 3, k = (k + 1) % 3)
		{
			if (tmp[i] < tmp[j] && tmp[j] < tmp[k])
				return true;
		}
		return false;
	};

	t[n] = 0, f[n] = -1;//undefined
	for (int i = n - 1; i >= 1; i--)
	{
		if (t[i + 1] == 0)
		{
			if (q[i] < q[i + 1])
				t[i] = 0, f[i] = -1;
			else
				t[i] = 1, f[i] = i + 1;
		}
		else
		{
			if (check(f[i + 1], i, i + 1))
				t[i] = t[i + 1], f[i] = f[i + 1];
			else
				t[i] = t[i + 1] + 1, f[i] = i + 1;
		}
	}
	cout << t[1] << '\n';
	return ;
}

int main()
{
	#ifdef LOCAL
	freopen("data.in", "r", stdin);
	freopen("mycode.out", "w", stdout);
	#endif

	ios :: sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
	
	#ifdef TestCases
	cin >> T;
	#endif
	
	while (T--)
		solve();
	return 0;
}