[CF23B]Party-构造

⚠写不出证明，只会找规律（悲
题目链接

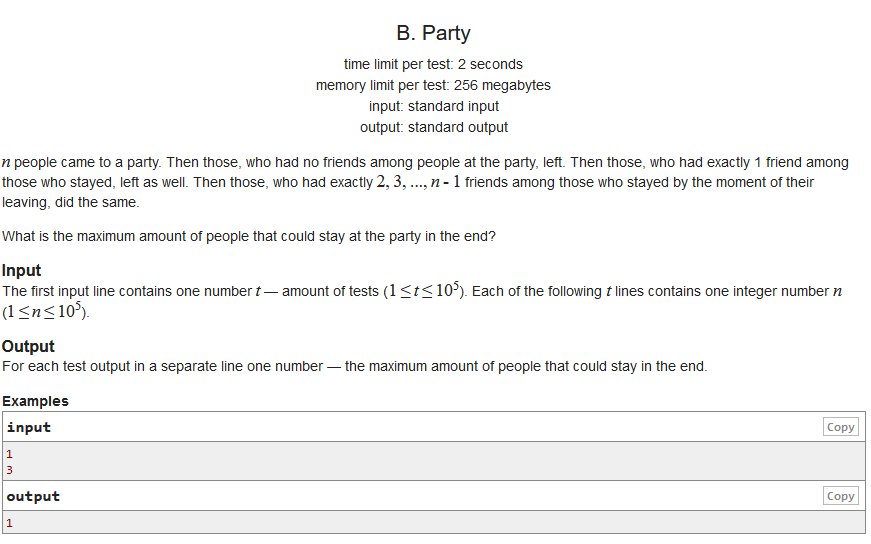
翻译：
有\(n\)个人来参加聚会，首先是没有朋友留在聚会上的人离开，然后有\(1\)个朋友留在聚会的人离开……
即，第\(m\)次离开的人在聚会上有\(m-1\)个朋友。
问最后最多留下来多少人？
多组数据
\(t\)
\(n1\)
…
\(ni\)
…
\(nt\)

---

每个人的朋友数是可以让我们进行构造的[温迪_欸嘿]

然后使用小数据进行一些分析

1. 当人数为1，第1次就会离开，留下0人（因为派对上没有朋友嘛）

---

2. 当人数为2:

• 若2人互相为朋友则一起在第2次（1个朋友）时离开
• 若2人不认识则会一起在第1次（0个朋友）时离开

---

3.当人数为3：

• 如果大家的关系是这样↓（绿色线代表为朋友）
  
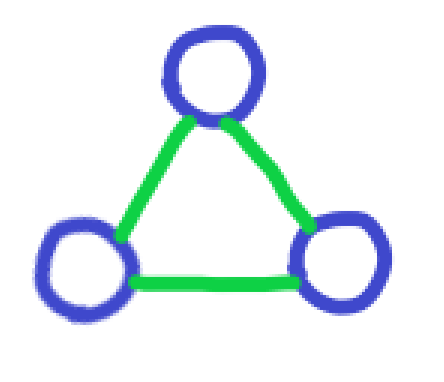
  那么大家都有1个朋友，都会在第3次离开

• 如果有2人不认识
  
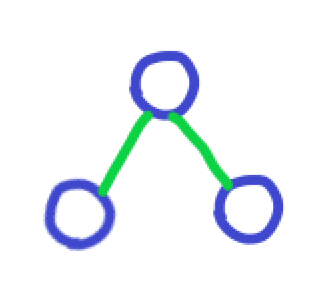
  第2次，有1个朋友的2人离开了
  但是第3次原本有2个朋友的人不用离开

  因为在第2次他的朋友离开了

  原本留在聚会朋友数：2
  现在留在聚会朋友数：0
  后面的离开需要的朋友数都会增加，所以这个人就是留在聚会啦（欸嘿

相信到这里构造思路已经体现了，让尽可能多的人因为朋友提前离开而留下，且提前离开人数尽可能少

4.当人数为4：
对于不可能情况大家自己模拟好了（抹泪）感觉没有必要说

• 如果大家都拥有3个朋友，那么都会在第4次离开（0，1，2同样）
• 如果情况如下图↓
  
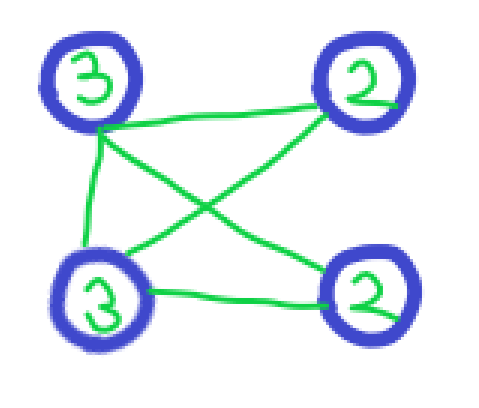
  那么2个朋友的人会在第3次离开，而3个朋友的人都变成了1个朋友，留下2人
  实际上这个就是最优的构造qwq

---

来点无意义小证明（或许算不上）：
设想：最优方案是1人提前离开，让接下来的所有人都朋友数-1（不可能情况）

所以找到“次优”方案，只需要其中1人互不认识，其他人都是朋友（绝对可行）

聚会一共\(n\)人，除去提前离开的2人，其他人都会最后留在聚会
所以程序：

#include <bits/stdc++.h>
using namespace std;
int main(){
	ios::sync_with_stdio(0);
	int t;
	cin >> t;
	while(t--){
		int n;
		cin >> n;
		if(n - 2 < 0){
			cout << 0;
		}else{
			cout << n-2;
		}
		cout << '\n'; 
	}
	return 0;
}

话说这道题当时给了我很大的构造自信，好像是第一道自己找的CF的构造qwq
顺便点名批评某外替艾曲上来打了一发等差数列。。。。