二次函数题目解析

2023.5.18

写给自己看的，以免明天的我忘记解法（雾

用了自己喜欢的讲解方法，适用于我[欸嘿]

-题目-

问$ ①$：

观察函数图像可得信息：

　1 .$  c > 0 $  (函数图像与$  y $交点位于 $  (0,c) $)
　2. $  a < 0 $  (函数开口向下时$ a$为负号)

　3.$ a$与$ b$异号 （$ a * b > 0$[同号]时,对称轴在$ y$轴左侧,右侧则为异号）

∵$ a < 0 , b > 0, c > 0$

∴$ abc < 0$

∴问$ ①$正确

问 $ ②$：

观察函数图像，当 $ x = -1$时 $ y < 0$;

将$ x = -1$代入一般式

∵$ a - b + c < 0 $

∵移项得 $ a + c < b$

∴故题中 $ b < a + c$ 错误

∴问$ ②$错误

问 $ ③$：

③：$ 4a + 2b + c > 0$

看作一元二次不等式

对称轴公式$ -b/2a$

∵$ -b/2a = 1 ($函数图像$)$

∴$ -b = 2a$

∴问$ ③ = 4a - 4a + c > 0$

∵$ c > 0$ (函数图像与$ y$轴交点位于$ (0,c)$)

∴问$ ③$正确

问$ ④$：

前情提要（雾）：对称轴公式$ -b/2a$，$ b < a + c$

∵$ b = -2a$

∵$ a - b + c < 0$

∴$ 1.5b - b + c < 0$

∴$ 2c - 3b < 0$（上式 * 2）

∴$ 2c < 3b$

问 $⑤$：

$ a + b > m(am + b)      (m != 1) $

可化为函数

$ a + b + c > m ^ 2a + mb + c$

观察函数图像发现，当$ m = 1$时达到最值 $ (x = m)$

题中条件有：$ x != 1$

∴问$ ⑤$正确，$ x(m)$取任何非1值都不为最值

即，$ ①③④⑤$正确

答案为 ： 4

 

写完了芜湖[温迪_撒花]

最近一直在学数学（躺）模拟赛时间都被数学霸占力

写点博客记录这段生活[温迪_欸嘿]

-----------------------------------------------------------------------

2023.5.19

穿越！

家人们还有几题，来写写解法芜湖

大概画一个函数图像[温迪_欸嘿]

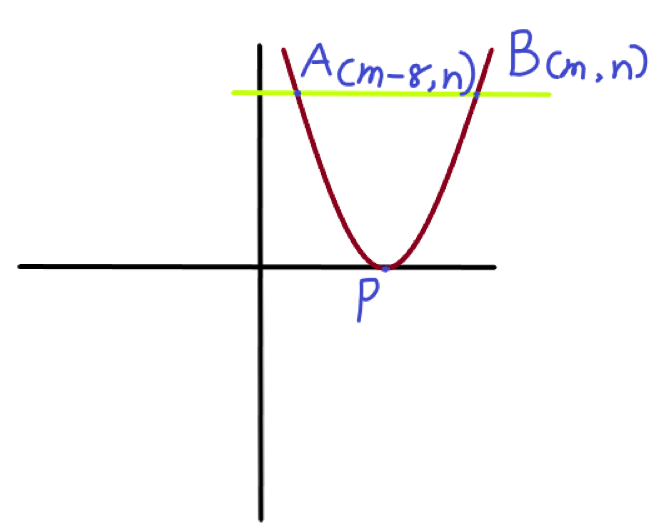
$P$为顶点

∵对称抽所在位置$x$坐标同时也为顶点所在的$x$轴坐标

∴$P((m + m - 8) / 2,0)$

∵顶点式 $y = a(x - h) + k      h为顶点x坐标，k为顶点y坐标$

因为题中a = 1

------化简后:$y = (x - (m - 4)) ^ 2 + 0 =( x - m + 4) ^ 2$

代入 $(m,n) :   n = (m - m - 4) ^ 2$

∴ $n = 16$

芜湖去吃饭了，等会继续写

-------------------------------------------------------------------------

意面能够点半份真的是太良心了，建议某丽姓中学食堂学一学

学来了的话罗勒叶少放一点emmmmm