loj6402 校门外的树(dp,多项式求逆)
庆祝一下,,,第一个我自己做出来的,,,多项式的题(没办法,我太弱
虽然用了2个小时才想出来,但这毕竟是0的突破……
首先声明,虽然我写的题解很长,但是大部分都是证明和废话
第一步,转化题意(用时30min):
一个1~n的全排列$p$,如果存在$i<j,p[i]<p[j]$,那么就把$i$和$j$之间连一条边。
问所有p的所有排列方案,最后联通块的大小的乘积,的和。
因为原题中$a$是随机的实数,所以说我们可以不用考虑有$a_i=a_j$的情况。
因为最后用到的只有相对的大小关系,所以可以直接转化成一个1~n的排列$p$。
其实很多时间都花在"诶,是这个意思吗,不会啊","哦,不对,看错题了"。
第二步,找规律推性质(用时50min):
我们发现,一个联通块,一定是$l$到$r$连续的一段。
假如说,$a$和$b$在同一个联通块内(令$a<b$),存在$c$满足$a<c<b$,并且$c$不在$a$和$b$所在联通块内。
我们来证明这种情况是不存在的。
首先,$p[b]<p[c]<p[a]$,否则$c$与$a$、$b$有直接的边相连。
那么$p[a]>p[b]$,但是他们在同一个联通块内,
所以一定存在一个位置$x$满足$x<a,p[x]<p[b]$或者$x>b,p[x]>p[a]$
那么$x$一定与$c$直接相连,所以证出矛盾。
同理,我们可以证到一个联通块的$p$也是连续的一段。
但是我不是这么找到这个性质的,因为我上面的方法只是证明了这个性质,但是如果我猜不到这个性质……
我按照套路思考,每个联通块找一个代表员好了,找谁呢,那就$p$最小的那个吧。
我们把点放在一个平面上,第$i$个点的坐标是$(i,p[i])$。
我们按照$p$从小到大,加入每个点。
首先,$p$最小的那个点加入的时候,我们考虑找它所在的联通块的点。
找到一个满足$p[j]>p[i]$的最大的$j$,那么$i$到$j$这个连续区间的所有点都在同一个联通块内。
(把这些点分成$p[x]<p[j]$,$p[x]>p[j]>p[i]$两种情况讨论就可以了)
然后$<i$的一些点,也可能在这个联通块内。
然后我们把这些点删掉,再找到$p$最小的那个点,递归下去。
我们发现,我们把一个n*n的矩形,一次一次的减去一个联通块所在的"势力范围",其实是一次一次砍掉了右边的一条和下面的一条,剩下的还是一个矩形。
如图:
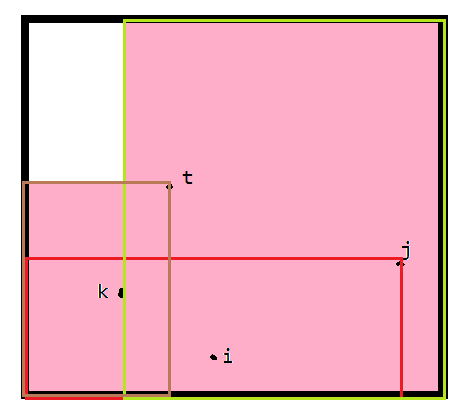
其中淡粉色是一个联通块的势力范围,$t$是这个联通块$p$最大的点,$k$是这个联通块最靠左(就是编号最小)的点。
我们再找下一个联通块的时候,下一个联通块势力范围一定是在白色部分。
所以下一个联通块的$p$最小的点的一定有$p[x]>p[t]$,编号最大的点$x<k$
于是我们两个性质都找到啦。
有了这两个性质之后,我们可以发现,一个联通块$[l,r]$,一定满足:$p[l],p[l+1],....,p[r-1],p[r]$一定是$n-l+1,n-(l+1)+1,....,n-r+1$的一个排列。
同时$p[1],p[2],....,p[r]$一定是$n,n-1,...,n-r+1$的一个排列。
同时$[l,r-1]$中不存在$x$满足$p[1],p[2],....,p[x]$是$n,n-1,....,n-x+1$的一个排列,否则就可以分出$[l,x],[x+1,r]$两个联通块了。
也就是说,如果我们称满足$p[1],p[2],....,p[x]$是$n,n-1,....,n-x+1$的一个排列的$x$是好的,那么每个$x$都一定是一个联通块的右端点。
第三步,推式子(用时40min):
有了上面的几个性质,我们可以开始列$dp$方程了。
我们令$f(n)$表示1~n的一个排列,除$n$位置外,不存在其他位置是好的,的方案数。
那么$f(0)=0,f(1)=1$
$f(n)=n!-\sum\limits_{i=1}^{n-1} i! f(n-i)$
令$g(n)=n!$,特别地,我们规定$g(0)=1$
那么$f(n)=g(n)-\sum\limits_{i=1}^{n-1} g(i) f(n-i)$
把$\sum$移到左边,可以得到$\sum\limits_{i=0}^{n} g(i) f(n-i) = g(n)$
我们发现这是一个卷积形式$f*g+1=g$。(因为$f(0)=0,g(0)=1$)
令$dp(i)$表示前$i$个数,并且$i$是一个联通块右端点,的贡献。规定$dp(0)=1$
枚举上一个联通块的右端点,那么有:
$dp(n)=\sum\limits_{i=0}^{n} (n-i) f(n-i) dp(i)$
令$h(n)=nf(n)$。$h(0)=0$
$dp(n)=\sum\limits_{i=0}^{n} h(n-i) dp(i)$
又是一个卷积形式$dp=dp*h+1$。(因为$h(0)=0,dp(0)=1$)
于是两次多项式求逆就可以解决问题啦。
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const ll mod=998244353,B=3;
const int maxn=1e7+7;
ll n,g[maxn],h[maxn],ginv[maxn],hinv[maxn],X[maxn];
template<typename T>void read(T& aa) {
aa=0;char cc=getchar();T ff=1;
while((cc!='-')&&(cc<'0'||cc>'9')) cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
ll qp(ll x,ll k) {
ll rs=1;
while(k) {
if(k&1) rs=rs*x%mod;
k>>=1; x=x*x%mod;
}
return rs;
}
ll finv(ll x) {return qp(x,mod-2);}
ll qp1(ll x,ll k) {
if(k<0) return qp(finv(x),-k);
return qp(x,k);
}
void Rader(ll F[],ll len) {
for(int i=1,j=len>>1,k;i<len-1;++i) {
if(i<j) swap(F[i],F[j]);
k=len>>1;
while(j>=k) {j-=k;k>>=1;}
if(j<k) j+=k;
}
}
void FFT(ll F[],ll len,ll on) {
Rader(F,len);
for(int h=2;h<=len;h<<=1) {
ll wn=qp1(B,(mod-1)*on/h);
for(int j=0;j<len;j+=h) {
ll w=1;
for(int i=j;i<j+h/2;++i) {
ll u=F[i],v=w*F[i+h/2]%mod;
F[i]=(u+v)%mod;
F[i+h/2]=(u-v+mod)%mod;
w=w*wn%mod;
}
}
}
ll x=finv(len);
if(on==-1) For(i,0,len) F[i]=F[i]*x%mod;
}
void get_inv(ll N,ll* A,ll* B) {
if(N==1) {
B[0]=finv(A[0]);
return;
}
get_inv((N+1)>>1,A,B);
ll n=1;for(;n<=(N<<1);n<<=1);
For(i,0,N-1) X[i]=A[i]; For(i,N,n) X[i]=B[i]=0;
FFT(X,n,1); FFT(B,n,1);
For(i,0,n) B[i]=B[i]*(2-B[i]*X[i]%mod+mod)%mod;
FFT(B,n,-1); For(i,N,n) B[i]=0;
}
int main() {
read(n);
g[0]=1; For(i,1,n) g[i]=g[i-1]*(ll)i%mod;
get_inv(n+1,g,ginv);
For(i,1,n) h[i]=ginv[i]*(ll)i%mod;
h[0]=1;
get_inv(n+1,h,hinv);
printf("%lld\n",hinv[n]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号