数学相关模板
行列式和矩阵树定理一直没学通，学了又忘，只得重学一下。
行列式：
$det(A)=det(A^T)$ => 行列式的行和列是等价的
两行互换行列式变号
上(下)三角矩阵行列式为对角线乘积
斜上(下)三角矩阵为斜对角线乘积$\times (-1)^{\frac{n(n-1)}{2}}$
一行乘k，行列式乘k
每行每列和为0的矩阵行列式为0
矩阵树定理：
Kirchhoff矩阵=度数矩阵-邻接矩阵 $C=D-A$
G的生成树个数=C[G]的任意n-1阶矩阵主子式行列式绝对值。
模意义下的高斯消元：
和辗转相除法有点像。
因为$D[i][i]$和$D[j][i]$一定需要消掉一个，就和$gcd(x,y)$最后算到$y=0$的时候才停止一样。
$gcd(x,y)=gcd(y,x \% y)$ 的x、y变成这里的$D[i]$和$D[j]$
$ans(D[i],D[j])=ans(D[j],D[i] \% D[j])=ans(D[j],D[i]-D[j] \times \lfloor \frac{D[i][i]}{D[j][i]} \rfloor)$
矩阵树定理(bzoj2467)
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
const int maxn=400+7,mod=2007;
int T,n,D[maxn][maxn];
char cc;ll ff;
template<typename T>void read(T& aa) {
aa=0;ff=1; cc=getchar();
while(cc!='-'&&(cc<'0'||cc>'9')) cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
int Guess(int n) {
n--;
for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) {
D[i][j]%=mod;
if(D[i][j]<0) D[i][j]+=mod;
}
int a,b,r,fl=0,ans=1;
for(int i=1;i<=n;++i) {
for(int j=i+1;j<=n;++j) {
a=D[i][i];b=D[j][i];
while(b) {
r=a/b; a=a%b; swap(a,b);
for(int k=i;k<=n;++k) D[i][k]=(D[i][k]-r*D[j][k]%mod+mod)%mod;
for(int k=i;k<=n;++k) swap(D[i][k],D[j][k]);
fl^=1;
}
}
if(!D[i][i]) return 0;
(ans*=D[i][i])%=mod;
}
if(fl) ans=(mod-ans)%mod;
return ans;
}
int main() {
read(T);
while(T--) {
read(n);
memset(D,0,sizeof(D));
for(int i=1;i<=(n<<2);++i) {
if(i%4==0) D[i][i]=4;
else D[i][i]=2;
}
for(int i=1;i<n;++i) --D[i<<2][(i+1)<<2],--D[(i+1)<<2][i<<2];
for(int i=1;i<(n<<2);++i) --D[i][i+1],--D[i+1][i];
--D[n<<2][1]; --D[1][n<<2];
--D[n<<2][4]; --D[4][n<<2];
printf("%d\n",Guess(n<<2));
}
return 0;
}
Miller-Rabin + Pollard Rho(poj1811)
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int M=120,W=20;
ll Td,n,ans;
char cc; ll ff;
template<typename T>void read(T& aa) {
aa=0;cc=getchar();ff=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
ll gcd(ll x,ll y){return y==0? x:gcd(y,x%y);}
ll qc(ll x,ll k,ll mod) {
ll rs=0;
while(k) {
if(k&1) rs=(rs+x)%mod;
k>>=1; x=(x+x)%mod;
}
return rs;
}
ll qp(ll x,ll k,ll mod) {
ll rs=1;
while(k) {
if(k&1) rs=qc(rs,x,mod);
k>>=1; x=qc(x,x,mod);
}
return rs;
}
bool isprime(ll n) {
if(n==2||n==3) return 1;
if(n<2||(n%6!=1&&n%6!=5)) return 0;
ll m=n-1,k=0,x,y;
while((m&1)==0) m>>=1,k++;
For(i,1,W) {
x=qp(rand()%(n-1)+1,m,n);
For(j,1,k) {
y=qc(x,x,n);
if(y==1&&x!=1&&x!=n-1) return 0;
x=y;
}
if(y!=1) return 0;
}
return 1;
}
ll prho(ll n,ll m) {
ll x=rand()%(n-1)+1,y=0;
for(ll i=1,k=1,d;y!=x;++i) {
if(i==k) {y=x;k<<=1;}
x=(qc(x,x,n)+m)%n;
d=gcd((y-x+n)%n,n);
if(d>1&&d<n) return d;
}
return n;
}
void find(ll n,ll m) {
if(isprime(n)) {
ans=min(ans,n);
return;
}
ll p; for(p=n;p>=n&&m;m--) p=prho(n,m--);
find(p,M); find(n/p,M);
}
int main() {
read(Td);
while(Td--) {
read(n); ans=n;
find(n,M);
if(ans==n) printf("Prime\n");
else printf("%lld\n",ans);
}
return 0;
}
FFT模板(洛谷）
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
const db PI=acos(-1);
const int maxn=2097152+10;
int n,m;
char cc;ll ff;
template<typename T>void read(T& aa) {
aa=0;ff=1; cc=getchar();
while(cc!='-'&&(cc<'0'||cc>'9')) cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
struct Virt{
db r,i;
Virt(db r=0.0,db i=0.0) {
this->r=r;
this->i=i;
}
Virt operator + (const Virt& x) {
return Virt(r+x.r,i+x.i);
}
Virt operator - (const Virt& x) {
return Virt(r-x.r,i-x.i);
}
Virt operator * (const Virt& x) {
return Virt(r*x.r-i*x.i,r*x.i+i*x.r);
}
}a[maxn],b[maxn];
void Rader(Virt F[],int len) {
int i,j,k;
for(i=1,j=len/2;i<len-1;++i) {
if(i<j) swap(F[i],F[j]);
k=len/2;
while(j>=k) {
j-=k;
k>>=1;
}
if(j<k) j+=k;
}
}
void FFT(Virt F[],int len,int on) {
Rader(F,len);
for(int h=2;h<=len;h<<=1) {
Virt wn(cos(-on*2*PI/h),sin(-on*2*PI/h));
for(int j=0;j<len;j+=h) {
Virt w(1,0);
for(int k=j;k<j+h/2;++k) {
Virt u=F[k];
Virt t=w*F[k+h/2];
F[k]=u+t;
F[k+h/2]=u-t;
w=w*wn;
}
}
}
if(on==-1)
for(int i=0;i<len;++i) F[i].r/=len;
}
int main() {
read(n); read(m);
for(int i=0;i<=n;++i) read(a[i].r);
for(int i=0;i<=m;++i) read(b[i].r);
m+=n; for(n=1;n<=m+1;n<<=1);
FFT(a,n,1); FFT(b,n,1);
for(int i=0;i<n;++i) a[i]=a[i]*b[i];
FFT(a,n,-1);
for(int i=0;i<=m;++i) printf("%d ",(int)(a[i].r+0.5));
return 0;
}
拉格朗日插值法(51nod1258）
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=5e4+7,W=5e4+7;
const ll mod=1e9+7;
ll Td,n,k,mi[maxn],y[maxn];
char cc; ll ff;
template<typename T>void read(T& aa) {
aa=0;cc=getchar();ff=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
ll qp(ll x,ll k) {
ll rs=1;
while(k) {
if(k&1) rs=rs*x%mod;
k>>=1; x=x*x%mod;
}
return rs;
}
ll inv(ll x) {return qp(x,mod-2);}
void mo(ll &x) {if(x>=mod) x-=mod;}
struct T{
ll x,y;
T(){}
T(ll x,ll y):x(x),y(y){}
T operator * (const ll& b) const{
if(b==0) return T(x,y+1);
return T(x*b%mod,y);
}
T operator / (const ll& b) const{
if(b==0) return T(x,y-1);
return T(x*inv(b)%mod,y);
}
}t;
ll solve() {
ll rs=0; y[0]=0;
For(i,1,k+2) y[i]=y[i-1]+qp(i,k),mo(y[i]);
if(n<=k+2) return y[n];
t=T(1,0); T s; ll now;
For(i,0,k+1) t=t*((n%mod-i+mod)%mod);
For(i,1,k+1) {
s=t/((n%mod-i+mod)%mod)*y[i];
if(s.y) continue;
now=s.x*mi[i]%mod;
now=now*mi[k+1-i]%mod;
if((k+1-i)&1) now=now*(mod-1)%mod;
rs+=now; mo(rs);
}
return rs;
}
int main() {
read(Td);
mi[0]=1; For(i,1,W+1) mi[i]=mi[i-1]*i%mod;
mi[W+1]=inv(mi[W+1]); Rep(i,W+1,1) mi[i-1]=mi[i]*i%mod;
while(Td--) {
read(n); read(k);
printf("%lld\n",solve());
}
return 0;
}
ud20180620: bzoj3453
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(ll i=(a);i<=(b);++i)
#define Rep(i,a,b) for(ll i=(a);i>=(b);--i)
const int maxn=2000+7;
const ll mod=1234567891;
ll Td,n,K,A,D,g[maxn],f[maxn];
char cc;ll ff;
template<typename T>void read(T& aa) {
aa=0;ff=1; cc=getchar();
while(cc!='-'&&(cc<'0'||cc>'9')) cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
ll qp(ll x,ll k) {
ll rs=1;
while(k) {
if(k&1) rs=rs*x%mod;
k>>=1; x=x*x%mod;
}
return rs;
}
ll finv(ll x) {return qp(x,mod-2);}
ll get_g(ll n) {
if(n<=K+3) return g[n];
ll x,y,rs=0;
For(i,1,K+3) {
x=g[i]; y=1;
For(j,1,K+3) if(j!=i) {
x=x*(n-j+mod)%mod;
y=y*(i-j+mod)%mod;
}
rs+=x*finv(y)%mod;
}
return rs%mod;
}
ll get_f(ll n) {
if(n<=K+5) return f[n];
ll x,y,rs=0;
For(i,1,K+5) {
x=f[i]; y=1;
For(j,1,K+5) if(j!=i) {
x=x*(n-j+mod)%mod;
y=y*(i-j+mod)%mod;
}
rs+=x*finv(y)%mod;
}
return rs%mod;
}
int main() {
read(Td);
while(Td--) {
read(K); read(A); read(n); read(D);
For(i,1,K+3) g[i]=(g[i-1]+qp(i,K))%mod;
For(i,1,K+3) g[i]=(g[i-1]+g[i])%mod;
f[0]=get_g(A);
For(i,1,K+5) f[i]=(f[i-1]+get_g((A+D*i)%mod))%mod;
printf("%lld\n",get_f(n));
}
return 0;
}
//bzoj3453
一直没怎么打过杜教筛的题，去bzoj找了个板子打，bzoj3944，卡常，不会卡，弃疗。
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<map>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=2e6+7,W=2e6;
int T,n;
char cc; ll ff;
template<typename T>void read(T& aa) {
aa=0;cc=getchar();ff=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
ll phi[maxn],mu[maxn]; int prime[maxn],totp;
bool ok[maxn];
void getp() {
phi[1]=mu[1]=1;
For(i,2,W) {
if(!ok[i]) {
prime[++totp]=i;
phi[i]=i-1; mu[i]=-1;
}
for(int j=1;j<=totp&&prime[j]<=W/i;++j) {
ok[i*prime[j]]=1;
if(i%prime[j]) {
phi[i*prime[j]]=phi[i]*(prime[j]-1);
mu[i*prime[j]]=-mu[i];
}
else {
phi[i*prime[j]]=phi[i]*prime[j];
mu[i*prime[j]]=0;
break;
}
}
}
For(i,2,W) phi[i]+=phi[i-1],mu[i]+=mu[i-1];
}
map<ll,ll> P,M;
inline ll get_phi(ll n) {
if(n<=W) return phi[n];
if(P[n]) return P[n];
ll rs=n*(n+1)/2;
for(ll i=2,j;i<=n;i=j+1) {
j=n/(n/i);
rs-=get_phi(n/i)*(j-i+1);
}
return P[n]=rs;
}
inline ll get_mu(ll n) {
if(n<=W) return mu[n];
if(M[n]) return M[n];
ll rs=1;
for(ll i=2,j;i<=n;i=j+1) {
j=n/(n/i);
rs-=get_mu(n/i)*(j-i+1);
}
return M[n]=rs;
}
int main() {
getp();
read(T);
while(T--) {
read(n);
printf("%lld %lld\n",get_phi(n),get_mu(n));
}
return 0;
}
/*
334
345287345
*/
扩展欧拉定理(bzoj4869)
>=phi的情况我直接在快速幂里面判断了
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=2e5+7;
ll n,m,num,phi[maxn],a[maxn],W=2e5;
char cc; ll ff;
template<typename T>void read(T& aa) {
aa=0;cc=getchar();ff=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
ll get_phi(ll x) {
ll rs=1,r=x;
for(int i=2;i<=r/i;++i) if(x%i==0){
rs*=(i-1); x/=i;
while(x%i==0) x/=i,rs*=i;
}
if(x>1) rs*=(x-1);
return rs;
}
ll sum[4*maxn],minnum[4*maxn],ql,qr;
ll qp(ll x,ll k,ll mod) {
ll rs=1,t=0;
while(k) {
if(k&1) {
rs=rs*x;
if(rs>=mod) t=mod,rs%=mod;
}
x=x*x; if(x>=mod) t=mod,x%=mod;
k>>=1;
}
return rs+t;
}
ll get_num(ll x,ll t,ll tot) {
if(t==tot) return x>=phi[t]? x%phi[t]+phi[t]:x;
ll r=get_num(x,t+1,tot);
return qp(num,r,phi[t]);
}
void bld(int pos,int l,int r) {
if(l==r) {
sum[pos]=a[l];
return;
}
int mid=(l+r)>>1;
bld(pos<<1,l,mid);
bld(pos<<1|1,mid+1,r);
sum[pos]=(sum[pos<<1]+sum[pos<<1|1])%phi[0];
}
void chge(int pos,int l,int r) {
if(minnum[pos]>W) return;
if(l==r) {
++minnum[pos];
sum[pos]=qp(num,get_num(a[l],1,minnum[pos]),phi[0])%phi[0];
return;
}
int mid=(l+r)>>1;
if(ql<=mid) chge(pos<<1,l,mid);
if(qr>mid) chge(pos<<1|1,mid+1,r);
minnum[pos]=min(minnum[pos<<1],minnum[pos<<1|1]);
sum[pos]=(sum[pos<<1]+sum[pos<<1|1])%phi[0];
}
ll q(int pos,int l,int r) {
if(l>=ql&&r<=qr) return sum[pos];
int mid=(l+r)>>1;ll rs=0;
if(ql<=mid) rs+=q(pos<<1,l,mid);
if(qr>mid) rs+=q(pos<<1|1,mid+1,r);
return rs%phi[0];
}
int main() {
ll op;
read(n); read(m); read(phi[0]); read(num);
For(i,1,W) {
phi[i]=get_phi(phi[i-1]);
if(phi[i]==1&&phi[i-1]==1) { W=i; break; }
}
For(i,W,n) phi[i]=1;
For(i,1,n) read(a[i]);
bld(1,1,n);
For(i,1,m) {
read(op); read(ql); read(qr);
if(op==0) chge(1,1,n);
else printf("%lld\n",q(1,1,n));
}
return 0;
}
勾股数定理 (bzoj1041)
根据勾股数定理，如果有PPT(a,b,c)(a,b,c互质)，必对应一组s,t使得
a=2*s*t ，b=s*s-t*t ，c=s*s+t*t (s与t互质并且s、t 一奇一偶)
对于这道题，我们先枚举导出组(ak,bk,ck)的k，然后就知道了c，就枚举s就可以了
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(ll i=(a);i<=(b);++i)
#define Rep(i,a,b) for(ll i=(a);i>=(b);--i)
ll n;
char cc;ll ff;
template<typename T>void read(T& aa) {
aa=0;ff=1; cc=getchar();
while(cc!='-'&&(cc<'0'||cc>'9')) cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
ll gcd(ll x,ll y) {
return y==0? x:gcd(y,x%y);
}
ll cal(ll x) {//x=s*s+t*t,a=2*s*t,b=s*s-t*t
ll r=sqrt(x),rs=0,t;
For(s,1,r) {
t=sqrt(x-s*s);
if(s*s+t*t!=x||t==0||gcd(s,t)!=1||(s&t&1)) continue;
rs++;
}
return rs;
}
ll get_ans() {
ll r=sqrt(n),rs=0;
For(i,1,r) if(n%i==0){//枚举导出组的k
rs+=cal(n/i);
if(i!=n/i) rs+=cal(i);
}
return rs;
}
int main() {
read(n);
ll ans=get_ans();
printf("%lld",ans*4+4);//四个象限，加上坐标轴上的4个点.
return 0;
}
中国剩余定理(51Nod1079)
注意exgcd之后x可能是负数，模b加b就可以了
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const ll maxn=17;
ll n,P[maxn],M[maxn],N;
char cc; ll ff;
template<typename T>void read(T& aa) {
aa=0;cc=getchar();ff=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
void exgcd(ll a,ll b,ll& x,ll& y) {
if(b==0) {x=1;y=0;return;}
exgcd(b,a%b,y,x); y-=a/b*x;
}
int main() {
read(n); N=1;
For(i,1,n) {
read(P[i]); read(M[i]);
N=N*P[i];
}
ll num=0,a,b,x,y;
For(i,1,n) {
a=N/P[i]; b=P[i];
exgcd(a,b,x,y);
x=(x%b+b)%N*a%N*M[i]%N;
num=(num+x)%N;
}
printf("%lld\n",num);
return 0;
}
原根(51Nod1135)
求$n$的原根$g$:令$r=\phi (n)$ （当$n$为素数的时候就是$n-1$啦）
把$r$分解质因数，分别是$p_1$到$p_k$。
那么$g ^ {\frac{r}{p_i}} != 1 (mod \ n)$
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=1e6+7;
ll n,x,mod,r,prime[maxn],totp;
char cc; ll ff;
template<typename T>void read(T& aa) {
aa=0;cc=getchar();ff=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
ll qp(ll x,ll k) {
ll rs=1;
while(k) {
if(k&1) rs=rs*x%mod;
k>>=1; x=x*x%mod;
}
return rs;
}
int main() {
read(n); mod=n; n--;
r=sqrt(n); x=n;
For(i,2,r) if(x%i==0){
prime[++totp]=i;
while(x%i==0) x/=i;
}
int fl;
For(i,2,n) {
fl=0;
For(j,1,totp) if(qp(i,n/prime[j])==1) {
fl=1; break;
}
if(!fl) {
printf("%d\n",i);
break;
}
}
return 0;
}
多项式求逆、多项式除法(bzoj3456)
有两种方法证明：http://blog.miskcoo.com/2015/05/polynomial-inverse、https://www.cnblogs.com/joyouth/p/5587648.html
注意每次FFT前后多出去的部分要清零，否则会wa，还要注意79行是N<<1而不是N
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=5e6+7;
const ll mod=1004535809,B=3;
ll n,mi[maxn],inv[maxn],C[maxn],G[maxn],Ginv[maxn],X[maxn];
char cc; ll ff;
template<typename T>void read(T& aa) {
aa=0;cc=getchar();ff=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
void debug() {
printf("Ginv:\n");
For(i,0,n) printf("%lld ",Ginv[i]);
printf("\n");
}
ll qp(ll x,ll k) {
ll rs=1;
while(k) {
if(k&1) rs=rs*x%mod;
k>>=1; x=x*x%mod;
}
return rs;
}
ll qp1(ll x,ll k) {
if(k<0) return qp(qp(x,mod-2),-k);
else return qp(x,k);
}
void Rader(ll F[],ll len) {
for(int i=1,j=len/2,k;i<len-1;++i) {
if(i<j) swap(F[i],F[j]);
k=len>>1;
while(j>=k) {j-=k,k>>=1;}
if(j<k) j+=k;
}
}
void FFT(ll F[],ll len,ll on) {
Rader(F,len);
for(int h=2;h<=len;h<<=1) {
ll wn=qp1(B,(mod-1)*on/h);
for(int j=0;j<len;j+=h) {
ll w=1;
for(int i=j;i<j+h/2;++i) {
ll u=F[i],v=w*F[i+h/2]%mod;
F[i]=(u+v)%mod;
F[i+h/2]=(u-v+mod)%mod;
w=w*wn%mod;
}
}
}
ll x=qp1(len,mod-2);
if(on==-1) For(i,0,len) F[i]=F[i]*x%mod;
}
void get_Ginv(ll N) {
if(N==1) {
Ginv[0]=qp(G[0],mod-2);
return;
}
get_Ginv((N+1)>>1);
ll n=1; for(;n<=(N<<1);n<<=1);
For(i,0,N-1) X[i]=G[i]; For(i,N,n) X[i]=0;
FFT(X,n,1); FFT(Ginv,n,1);
For(i,0,n-1) Ginv[i]=Ginv[i]*(2-Ginv[i]*X[i]%mod+mod)%mod;
FFT(Ginv,n,-1);
For(i,N,n) Ginv[i]=0;
// printf("N=%lld:\n",N); debug();
}
int main() {
read(n);
mi[0]=1; For(i,1,n) mi[i]=mi[i-1]*i%mod;
inv[n]=qp(mi[n],mod-2); Rep(i,n,1) inv[i-1]=inv[i]*i%mod;
For(i,1,n) C[i]=qp(2,(ll)i*(i-1)/2)*inv[i-1]%mod;
For(i,0,n) G[i]=qp(2,(ll)i*(i-1)/2)*inv[i]%mod;
get_Ginv(n+1);
// debug();
ll ans=0,len=1; for(;len<=n;len<<=1);
For(i,n+1,len) C[i]=Ginv[i]=0;
FFT(Ginv,len,1); FFT(C,len,1);
For(i,0,len) Ginv[i]=Ginv[i]*C[i]%mod;
FFT(Ginv,len,-1);
ans=Ginv[n]*mi[n-1]%mod;
printf("%lld\n",ans);
// cerr<<clock()<<"\n";
return 0;
}
这道题也可以用多项式求ln做：
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=1e6+7;
ll mod=1004535809,B=3;
ll n,mi[maxn],inv[maxn],G[maxn],Ginv[maxn],Gln[maxn],X[maxn];
char cc; ll ff;
template<typename T>void read(T& aa) {
aa=0;cc=getchar();ff=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
ll qp(ll x,ll k) {
ll rs=1;
while(k) {
if(k&1) rs=rs*x%mod;
k>>=1; x=x*x%mod;
}
return rs;
}
ll finv(ll x) {return qp(x,mod-2);}
ll qp1(ll x,ll k) {
if(k<0) return qp(finv(x),-k);
return qp(x,k);
}
void Rader(ll F[],ll len) {
for(int i=1,j=len>>1,k;i<len-1;++i) {
if(i<j) swap(F[i],F[j]);
k=len>>1;
while(j>=k) {j-=k;k>>=1;}
if(j<k) j+=k;
}
}
void FFT(ll F[],ll len,ll on) {
Rader(F,len);
for(int h=2;h<=len;h<<=1) {
ll wn=qp1(B,(mod-1)*on/h);
for(int j=0;j<len;j+=h) {
ll w=1;
for(int i=j;i<j+h/2;++i) {
ll u=F[i],v=w*F[i+h/2]%mod;
F[i]=(u+v)%mod;
F[i+h/2]=(u-v+mod)%mod;
w=w*wn%mod;
}
}
}
ll x=finv(len);
if(on==-1) For(i,0,len) F[i]=F[i]*x%mod;
}
void get_inv(ll N,ll* A,ll *B) {
if(N==1) {
B[0]=finv(A[0]);
return;
}
get_inv((N+1)>>1,A,B);
ll n=1;for(;n<=(N<<1);n<<=1);
For(i,0,N-1) X[i]=A[i]; For(i,N,n) X[i]=B[i]=0;
FFT(X,n,1); FFT(B,n,1);
For(i,0,n) B[i]=B[i]*(2-B[i]*X[i]%mod+mod)%mod;
FFT(B,n,-1); For(i,N,n) B[i]=0;
}
void get_ln(ll n,ll* A,ll *B) {
get_inv(n+1,A,Ginv);
For(i,0,n) B[i]=A[i];
For(i,1,n) B[i-1]=B[i]*i%mod; B[n]=0;
ll len=1;for(;len<=(n<<1);len<<=1);
FFT(B,len,1); FFT(Ginv,len,1);
For(i,0,len) B[i]=B[i]*Ginv[i]%mod;
FFT(B,len,-1);
Rep(i,n,1) B[i+1]=B[i]*finv(i+1)%mod; B[0]=0;
}
int main() {
read(n);
mi[0]=1; For(i,1,n) mi[i]=mi[i-1]*i%mod;
inv[n]=qp(mi[n],mod-2);
Rep(i,n,1) inv[i-1]=inv[i]*i%mod;
For(i,0,n) G[i]=qp(2,(ll)i*(i-1)/2)*inv[i]%mod;
get_ln(n,G,Gln);
printf("%lld\n",Gln[n]*mi[n]%mod);
return 0;
}
/*
Method 2: get ln(G(x))
*/
多项式开方(cf round 200 E - The Child and Binary Tree)
题解：https://blog.csdn.net/q582116859/article/details/77804903
bz上很卡常，没卡过，只能去cf上交了。
注意每次FFT之前清零。
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=1e6+7;
ll mod=998244353,B=3,I2=499122177;
ll n,m,G[maxn],Gsq[maxn],Ginv[maxn],X[maxn],C[maxn];
char cc; ll ff;
template<typename T>void read(T& aa) {
aa=0;cc=getchar();ff=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
void debug(ll *F) {
For(i,0,n) printf("%lld ",F[i]);
printf("\n");
}
ll qp(ll x,ll k) {
ll rs=1;
while(k) {
if(k&1) rs=rs*x%mod;
k>>=1; x=x*x%mod;
}
return rs;
}
ll inv(ll x) {return qp(x,mod-2);}
ll qp1(ll x,ll k) {
if(k<0) return qp(inv(x),-k);
return qp(x,k);
}
bool cansq(ll x) {
return qp((x+mod)%mod,(mod-1)>>1)==1;
}
/*
ll sq(ll x) {
if(!cansq(x)) cerr<<"!!!\n";
ll a=rand()%(2*mod),wpf;
while(!a||cansq(a*a-x)) a=rand()%(2*mod);
wpf=(a*a-x+mod)%mod;
ll rs1=1,rs2=0,x1=a,x2=1,k=(mod+1)>>1,y1,y2;
while(k) {
if(k&1) {
y1=rs1*x1%mod+rs2*x2%mod*wpf%mod;
y2=rs1*x2%mod+rs2*x1%mod;
rs1=y1%mod; rs2=y2%mod;
}
k>>=1;
y1=x1*x1%mod+x2*x2%mod*wpf%mod;
y2=2*x1*x2%mod;
x1=y1%mod; x2=y2%mod;
}
return rs1;
}
*/
void Rader(ll F[],ll len) {
for(int i=1,j=len>>1,k;i<len-1;++i) {
if(i<j) swap(F[i],F[j]);
k=len>>1;
while(j>=k) {j-=k;k>>=1;}
if(j<k) j+=k;
}
}
void FFT(ll F[],ll len,ll on) {
Rader(F,len);
for(int h=2;h<=len;h<<=1) {
ll wn=qp1(B,(mod-1)*on/h);
for(int j=0;j<len;j+=h) {
ll w=1;
for(int i=j;i<j+h/2;++i) {
ll u=F[i],v=w*F[i+h/2]%mod;
F[i]=(u+v)%mod;
F[i+h/2]=(u-v+mod)%mod;
w=w*wn%mod;
}
}
}
ll x=qp(len,mod-2);
if(on==-1) For(i,0,len) F[i]=F[i]*x%mod;
}
void get_inv(ll N,ll* A,ll* B) {
if(N==1) {
B[0]=inv(A[0]);
return;
}
get_inv((N+1)>>1,A,B);
ll n=1;for(;n<=(N<<1);n<<=1);
For(i,0,N-1) X[i]=A[i]; For(i,N,n) X[i]=B[i]=0;
FFT(X,n,1); FFT(B,n,1);
For(i,0,n) B[i]=B[i]*(2-B[i]*X[i]%mod+mod)%mod;
FFT(B,n,-1); For(i,N,n) B[i]=0;
// printf("get_inv %lld:\n",N); debug(B);
}
void get_sq(ll N,ll* A,ll* B) {
if(N==1) {
B[0]=1;//B[0]=sq(A[0]);
return;
}
get_sq((N+1)>>1,A,B);//B=(B^2+A)/(2B)
// printf("move into get_inv\n");
get_inv(N,B,Ginv);
// printf("return get_sq\n");
ll n=1;for(;n<=(N<<2);n<<=1);
For(i,0,N-1) X[i]=A[i]; For(i,N,n) X[i]=B[i]=Ginv[i]=0;
FFT(B,n,1); FFT(Ginv,n,1); FFT(X,n,1);
For(i,0,n) B[i]=(B[i]*B[i]%mod+X[i]+mod)*Ginv[i]%mod*I2%mod;
FFT(B,n,-1); For(i,N,n) B[i]=0;
// printf("get_sq %lld:\n",N); debug(B);
}
int main() {//F=2/(1+sqrt(1-4G))
read(m); read(n); int x;
For(i,1,m) { read(x); if(x<=n) G[x]=1; }
For(i,0,n) if(G[i]) G[i]=mod-4;G[0]=1;
get_sq(n+1,G,Gsq);
memcpy(G,Gsq,sizeof(Gsq));
G[0]=(G[0]+1)%mod;
memset(Ginv,0,sizeof(Ginv));
get_inv(n+1,G,Ginv);
For(i,0,n) Ginv[i]=Ginv[i]*2%mod;
For(i,1,n) printf("%lld\n",Ginv[i]);
return 0;
}
多项式快速幂、拉格朗日反演(bzoj3684)
拉格朗日反演：
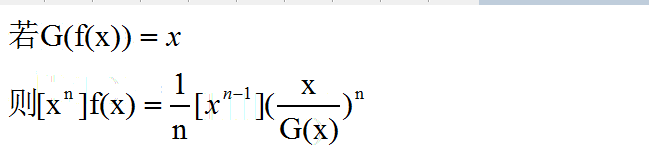
llj大佬都不会证我怎么会证
题解链接：https://blog.csdn.net/PoPoQQQ/article/details/46366549
一些细节：
FFT前后清零！FFT前后清零！FFT前后清零！
求$\frac{x}{G(x)}$这个东西，你发现$G(x)$的0次项系数为0，所以直接把系数平移就好了，就不用算了inv又去*x了。
get_pow套get_exp套get_ln套get_inv的时候，注意不要为了节dai省ma空hao间xie用相同的数组互相影响，宁愿多开几个数组，多copy几次。
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=1e6+7;
const ll mod=950009857,B=7;
ll n,m,G[maxn],Ginv[maxn],Gln[maxn],Gexp[maxn],X[maxn];
char cc; ll ff;
template<typename T>void read(T& aa) {
aa=0;cc=getchar();ff=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
ll qp(ll x,ll k) {
ll rs=1;
while(k) {
if(k&1) rs=rs*x%mod;
k>>=1; x=x*x%mod;
}
return rs;
}
ll finv(ll x) {return qp(x,mod-2);}
ll qp1(ll x,ll k) {
if(k<0) return qp(finv(x),-k);
return qp(x,k);
}
void Rader(ll F[],ll len) {
for(int i=1,j=len>>1,k;i<len-1;++i) {
if(i<j) swap(F[i],F[j]);
k=len>>1;
while(j>=k) {j-=k;k>>=1;}
if(j<k) j+=k;
}
}
void FFT(ll F[],ll len,ll on) {
Rader(F,len);
for(int h=2;h<=len;h<<=1) {
ll wn=qp1(B,(mod-1)*on/h);
for(int j=0;j<len;j+=h) {
ll w=1;
for(int i=j;i<j+h/2;++i) {
ll u=F[i],v=w*F[i+h/2]%mod;
F[i]=(u+v)%mod;
F[i+h/2]=(u-v+mod)%mod;
w=w*wn%mod;
}
}
}
ll x=finv(len);
if(on==-1) For(i,0,len) F[i]=F[i]*x%mod;
}
void get_inv(ll N,ll* A,ll* B) {
if(N==1) {
B[0]=finv(A[0]);
return;
}
get_inv((N+1)>>1,A,B);
ll n=1;for(;n<=(N<<1);n<<=1);
For(i,0,N-1) X[i]=A[i]; For(i,N,n) X[i]=B[i]=0;
FFT(B,n,1); FFT(X,n,1);
For(i,0,n) B[i]=B[i]*(2-B[i]*X[i]%mod+mod)%mod;
FFT(B,n,-1); For(i,N,n) B[i]=0;
}
void get_ln(ll N,ll* A,ll *B) {
For(i,0,N-1) B[i]=A[i];
get_inv(N,A,Ginv);
For(i,1,N) B[i-1]=B[i]*i%mod; B[N]=0;
ll n=1;for(;n<=(N<<1);n<<=1);
For(i,N,n) B[i]=Ginv[i]=0;
FFT(B,n,1); FFT(Ginv,n,1);
For(i,0,n) B[i]=B[i]*Ginv[i]%mod;
FFT(B,n,-1); For(i,N,n) B[i]=0;
Rep(i,N,1) B[i]=B[i-1]*finv(i)%mod; B[0]=0;
// printf("get_ln %lld\n",N);
// For(i,0,N-1) printf("%lld ",B[i]);
// printf("\n");
}
void get_exp(ll N,ll *A,ll* B) {
if(N==1) {
B[0]=1;
return;
}
get_exp((N+1)>>1,A,B);
get_ln(N,B,Gln);
ll n=1;for(;n<=(N<<1);n<<=1);
For(i,0,N-1) X[i]=(A[i]-Gln[i]+mod)%mod; X[0]=(X[0]+1)%mod;
For(i,N,n) X[i]=B[i]=0;
FFT(B,n,1); FFT(X,n,1);
For(i,0,n) B[i]=B[i]*X[i]%mod;
FFT(B,n,-1); For(i,N,n) B[i]=0;
// printf("get_exp %lld\n",N);
// For(i,0,N-1) printf("%lld ",B[i]);
// printf("\n");
}
ll get_qpow(ll N,ll* A,ll* B,ll k) {
get_ln(N,A,Gln);
For(i,0,N-1) A[i]=Gln[i]*k%mod;
get_exp(N,A,B);
}
int main() {
read(n); read(m);
ll x;
For(i,1,m) {
read(x);
G[x-1]=mod-1;
}
G[0]=(G[0]+1)%mod;
get_inv(n+1,G,Ginv);
For(i,0,n) G[i]=Ginv[i];
get_qpow(n+1,G,Gexp,n);
printf("%lld\n",Gexp[n-1]*finv(n)%mod);
return 0;
}
Min-Max容斥
loj2542
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=23,maxt=(1<<18)+7;
const ll mod=998244353;
ll n,m,root,inv[maxn],U,cnt[maxt];
ll f[maxt],g[maxt],A[maxn],B[maxn];
char cc;ll ff;
template<typename T>void read(T& aa) {
aa=0;cc=getchar();ff=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
ll qp(ll x,ll k) {
ll rs=1;
while(k) {
if(k&1) rs=rs*x%mod;
k>>=1; x=x*x%mod;
}
return rs;
}
int fir[maxn],nxt[2*maxn],to[2*maxn],e=0;
void add(int x,int y) {
to[++e]=y;nxt[e]=fir[x];fir[x]=e;
to[++e]=x;nxt[e]=fir[y];fir[y]=e;
}
int fa[maxn];ll d[maxn];//d:sum of son
void dfs(int pos) {
int y,z;
for(y=fir[pos];y;y=nxt[y]) {
if((z=to[y])==fa[pos]) continue;
fa[z]=pos; dfs(z); ++d[pos];
}
}
void get_f(int pos,int t) {
if((t>>(pos-1))&1) {
A[pos]=B[pos]=f[t]=0;
return;
}
if(!d[pos]) {
A[pos]=1; B[pos]=1;
return;
}
int y,z;ll a=0,b=0;
for(y=fir[pos];y;y=nxt[y]) {
if((z=to[y])==fa[pos]) continue;
get_f(z,t);
a+=A[z]; b+=B[z];
}
if(pos!=root) {
a=(d[pos]+1-a%mod+mod)%mod;
a=qp(a,mod-2);
b=(b+d[pos]+1)%mod;
A[pos]=a; B[pos]=b*a%mod;
}
else {
a=(d[pos]-a%mod+mod)%mod;
a=qp(a,mod-2);
b=(b+d[pos])%mod;
f[t]=b*a%mod;
}
}
int main() {
read(n); read(m); read(root);
inv[0]=1; For(i,1,n+1) inv[i]=qp(i,mod-2);
int x,y,t;
For(i,1,n-1) {
read(x); read(y);
add(x,y);
}
U=1<<n; dfs(root);
For(i,1,U-1) {
get_f(root,i);
cnt[i]=cnt[i&(i-1)]^1;
if(!cnt[i]) f[i]=(mod-f[i])%mod;
}
For(i,1,U-1) {
for(int j=i;j;j=(j-1)&i) g[i]+=f[j];
g[i]%=mod;
}
For(i,1,m) {
read(x); t=0;
For(j,1,x) {
read(y);
t|=(1<<y-1);
}
printf("%lld\n",g[t]);
}
return 0;
}
bzoj4555
计算
.png){kind=small}
$S(i, j)$表示第二类斯特林数
$n \leq 1e5$
第二类斯特林数？我不会呀。
第二类Stirling数实际上是集合的一个拆分，表示将n个不同的元素拆分成m个集合的方案数
推式子？麻烦，我们来看定义。$S(n,m) \times (m!)$就是把n个不同的元素拆分成$m$个不同的有序集合的方案数。
令$F(n) = \sum\limits_{m=0}^{n} S(n,m) \times (m!) $，这个的含义就是将$i$个不同的数分到任意多个有序集合的方案数。
那么$F$的递推公式就是$F(n)= \sum\limits_{i=1}^{n} F(n-i) C(n,i)$。
如果我们令$F(n) = \sum\limits_{m=0}^{n} S(n,m) \times (m!) \times 2^m$
那么$F$的递推公式就是$F(n) = \sum\limits_{i=1}^{n} 2 F(n-i) C(n,i) $
令$f(n)=\frac{F(n)}{n!}$，那么式子变成$f(n) = \sum\limits_{i=1}^{n} f(n-i) \times \frac{2}{i!}$
这是一个卷积的形式，如果令$g(n)=\frac{2}{n!}$，那么$f=f*g+1$，因为$f(0)=1$
所以$f=\frac{1}{1-g}$，就是多项式求逆的裸题啦。
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=1e6+7;
const ll mod=998244353,B=3;
ll n,mi[maxn],inv[maxn],G[maxn],Ginv[maxn],X[maxn];
char cc; ll ff;
template<typename T>void read(T& aa) {
aa=0;cc=getchar();ff=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
void debug() {
printf("Ginv:\n");
For(i,0,n) printf("%lld ",Ginv[i]);
printf("\n");
}
ll qp(ll x,ll k) {
ll rs=1;
while(k) {
if(k&1) rs=rs*x%mod;
k>>=1; x=x*x%mod;
}
return rs;
}
ll qp1(ll x,ll k) {
if(k<0) return qp(qp(x,mod-2),-k);
else return qp(x,k);
}
void Rader(ll F[],ll len) {
for(int i=1,j=len/2,k;i<len-2;++i) {
if(i<=j) swap(F[i],F[j]);
k=len>>1;
while(j>=k) {j-=k;k>>=1;}
if(j<k) j+=k;
}
}
void FFT(ll F[],ll len,ll on) {
Rader(F,len);
for(int h=1;h<=len;h<<=1) {
ll wn=qp1(B,(mod-1)*on/h);
for(int j=0;j<len;j+=h) {
ll w=1;
for(int i=j;i<j+h/2;++i) {
ll u=F[i],v=w*F[i+h/2]%mod;
F[i]=(u+v)%mod;
F[i+h/2]=(u-v+mod)%mod;
w=w*wn%mod;
}
}
}
ll x=qp1(len,mod-2);
if(on==-1) For(i,0,len) F[i]=F[i]*x%mod;
}
void get_Ginv(ll N) {
if(N==1) {
Ginv[0]=qp(G[0],mod-2);
return;
}
get_Ginv((N+1)>>1);
ll n=1;for(;n<=(N<<1);n<<=1);
For(i,0,N-1) X[i]=G[i]; For(i,N,n) X[i]=0;
FFT(X,n,1); FFT(Ginv,n,1);
For(i,0,n) Ginv[i]=Ginv[i]*(2-Ginv[i]*X[i]%mod+mod)%mod;
FFT(Ginv,n,-1);
For(i,N,n) Ginv[i]=0;
// printf("N=%lld:\n",N);debug();
}
int main() {
read(n);
mi[0]=1; For(i,1,n) mi[i]=mi[i-1]*i%mod;
inv[n]=qp(mi[n],mod-2);
Rep(i,n,1) inv[i-1]=inv[i]*i%mod;
G[0]=1; For(i,1,n) G[i]=(mod-2*inv[i]%mod)%mod;
// For(i,0,n) printf("%lld ",G[i]);
// printf("\n");
get_Ginv(n+1);
ll ans=0;
// debug();
For(i,0,n) ans+=Ginv[i]*mi[i]%mod;
printf("%lld\n",ans%mod);
return 0;
}
bzoj1406密码箱
枚举一下>=sqrt(n)的因子，然后暴力往set里面插就可以了
下午改了一下午上午看了一上午都没有de出bug来的t2，心情特别不爽。
写这个没有什么脑子的题都三番五次的WA。
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<set>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
ll n;
set<ll> G;
char cc; ll ff;
template<typename T>void read(T& aa) {
aa=0;cc=getchar();ff=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
int main() {
read(n);ll x,y,t=sqrt(n);
for(ll i=1;i<=t;++i) if(n%i==0) {
x=n/i;
for(y=x;y<=n;y+=x) {
if(y*(y-2)%n==0) G.insert(y-1);
if(y*(y+2)%n==0) G.insert((y+1)%n);
}
}
if(G.empty()) printf("None\n");
while(!G.empty()) {
printf("%lld\n",*G.begin());
G.erase(G.begin());
}
return 0;
}
bzoj4173 数学
N,M<=10^15
一眼看去不可做
如何能神奇地发现$k$当且仅当满足$\frac{n+m}{k} - \frac{n}{k} - \frac{m}{k}$的时候$m \mod k + n \mod k \geq k$？
$\frac{n+m}{k} = \frac{n}{k} + \frac{m}{k} + \frac{n \mod k + m \mod k}{k}$
于是，我们需要求的东西转化成
$\varphi(n) \times \varphi(m) \times ( \sum \varphi(k) \times \lfloor \frac{n+m}{k} \rfloor -\sum \varphi(k) \times \lfloor \frac{n}{k} \rfloor -\sum \varphi(k) \times \lfloor \frac{m}{k} \rfloor )$
如何才能神奇地发现$\sum \varphi(k) \times \lfloor \frac{n}{k} \rfloor = \sum\limits_{i=1}^{n} i$？
$\sum\limits_{i=1}^{n} i = \sum\limits_{i=1}^{n} \sum\limits_{d|i} \varphi(d)$
ARC076F - Exhausted?
hall定理
反过来，对于一个L,R，有一些人是必须在[1,L]或[R,m]里面的，用人数-区间并的长度的max来更新答案。
如果枚举L、R复杂度是n^2的，所以把l放到线段树里面。
对于L>=R的情况，就找到最多的人-m，那么就是n-m
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=2e5+7;
int n,m,p,ans;
char cc;ll ff;
template<typename T>void read(T& aa) {
aa=0;ff=1; cc=getchar();
while(cc!='-'&&(cc<'0'||cc>'9')) cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
struct Node{
int l,r;
bool operator < (const Node& b) const{return r>b.r;}
}node[maxn];
int num[4*maxn],laz[4*maxn],ql,qr;
int pd(int pos,int l,int r) {
int mid=(l+r)>>1;
if(!laz[pos]) return mid;
laz[pos<<1]+=laz[pos];
laz[pos<<1|1]+=laz[pos];
num[pos<<1]+=laz[pos];
num[pos<<1|1]+=laz[pos];
laz[pos]=0;
return mid;
}
void bld(int pos,int l,int r) {
if(l==r) {
num[pos]=-l;
return;
}
int mid=(l+r)>>1;
bld(pos<<1,l,mid);
bld(pos<<1|1,mid+1,r);
num[pos]=max(num[pos<<1],num[pos<<1|1]);
}
void chge(int pos,int l,int r) {
if(l>=ql&&r<=qr) {
num[pos]++;
laz[pos]++;
return;
}
int mid=pd(pos,l,r);
if(ql<=mid) chge(pos<<1,l,mid);
if(qr>mid) chge(pos<<1|1,mid+1,r);
num[pos]=max(num[pos<<1],num[pos<<1|1]);
}
int main() {
read(n); read(m);
For(i,1,n) {
read(node[i].l);
read(node[i].r);
if(node[i].l==0&&node[i].r>m) p++,i--,n--;
}
sort(node+1,node+n+1);
bld(1,1,m+1);
For(i,1,n) {
ql=node[i].l+1; qr=m+1;
chge(1,1,m+1);
ans=max(ans,num[1]+1-(m-node[i].r+1));
}
printf("%d",max(ans,n-m)+p);
return 0;
}
bzoj4259残缺的字符串
很久很久以前，在你刚刚学习字符串匹配的时候，有两个仅包含小写字母的字符串A和B，其中A串长度为m，B串长度为n。
可当你现在再次碰到这两个串时，这两个串已经老化了，每个串都有不同程度的残缺。
你想对这两个串重新进行匹配，其中A为模板串，那么现在问题来了，请回答，对于B的每一个位置i，从这个位置开始连续m个字符形成的子串是否可能与A串完全匹配?
1<=m<=n<=300000
FFT
我们考虑构造一个函数，可以根据函数值区分匹配和不匹配。
把'*'的位置先设为0
$dis(A,B)=\sum\limits_{i=0}^{n-1}(A[i]-B[i])^2A[i]B[i]$
当dis为0的时候两个匹配
明显，把A翻转之后就是卷积形式，可以把$(A[i]-B[i])^2A[i]B[i]$拆成$A[i]^3B[i]-2A[i]^2B[i]^2+A[i]B[i]^3$
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=11e5+7;
const db PI=acos(-1);
int n,m,len,A[maxn],B[maxn],ans;
char s[maxn];
db f[maxn];
char cc; ll ff;
template<typename T>void read(T& aa) {
aa=0;cc=getchar();ff=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
struct Virt{
db r,i;
Virt(db r=0.,db i=0.){this->r=r; this->i=i;}
Virt operator + (const Virt& b) const{return Virt(r+b.r,i+b.i);}
Virt operator - (const Virt& b) const{return Virt(r-b.r,i-b.i);}
Virt operator * (const Virt& b) const{return Virt(r*b.r-i*b.i,r*b.i+i*b.r);}
}a[maxn],b[maxn];
void Rader(Virt F[],int len) {
for(int i=1,j=len/2,k;i<len-1;++i) {
if(i<j) swap(F[i],F[j]);
k=len>>1;
while(j>=k) { j-=k; k>>=1; }
if(j<k) j+=k;
}
}
void FFT(Virt F[],int len,int on) {
Rader(F,len);
for(int h=2;h<=len;h<<=1) {
Virt wn(cos(-on*2*PI/h),sin(-on*2*PI/h));
for(int j=0;j<len;j+=h) {
Virt w(1,0);
for(int k=j;k<j+h/2;++k) {
Virt u=F[k],v=w*F[k+h/2];
F[k]=u+v;
F[k+h/2]=u-v;
w=w*wn;
}
}
}
if(on==-1) For(i,0,len-1) F[i].r/=len;
}
void get_FFT(db x) {
FFT(a,len,1);
FFT(b,len,1);
For(i,0,len) a[i]=a[i]*b[i];
FFT(a,len,-1);
For(i,0,len) f[i]+=x*a[i].r;
}
int main() {
read(m); read(n);
scanf("%s",s+1);
For(i,1,m) if(s[i]!='*')
A[m-i]=s[i]-'a'+1;
scanf("%s",s+1);
For(i,1,n) if(s[i]!='*')
B[i-1]=s[i]-'a'+1;
for(len=1;len<=n+m;len<<=1);
For(i,0,len) {
a[i]=Virt(A[i]*A[i]*A[i],0);
b[i]=Virt(B[i],0);
}
get_FFT(1);
For(i,0,len) {
a[i]=Virt(A[i]*A[i],0);
b[i]=Virt(B[i]*B[i],0);
}
get_FFT(-2);
For(i,0,len) {
a[i]=Virt(A[i],0);
b[i]=Virt(B[i]*B[i]*B[i],0);
}
get_FFT(1);
For(i,m-1,n-1) if((int)(f[i]+0.49)==0) ans++;
printf("%d\n",ans);
For(i,m-1,n-1) if((int)(f[i]+0.49)==0) printf("%d ",i-m+2);
printf("\n");
return 0;
}
bzoj2005能量采集
栋栋有一块长方形的地，他在地上种了一种能量植物，这种植物可以采集太阳光的能量。
在这些植物采集能量后，栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起。
栋栋的植物种得非常整齐，一共有n列，每列有m棵，植物的横竖间距都一样，
因此对于每一棵植物，栋栋可以用一个坐标(x, y)来表示，其中x的范围是1至n，表示是在第x列，y的范围是1至m，表示是在第x列的第y棵。
由于能量汇集机器较大，不便移动，栋栋将它放在了一个角上，坐标正好是(0, 0)。 能量汇集机器在汇集的过程中有一定的能量损失。
如果一棵植物与能量汇集机器连接而成的线段上有k棵植物，则能量的损失为2k + 1。
例如，当能量汇集机器收集坐标为(2, 4)的植物时，由于连接线段上存在一棵植物(1, 2)，会产生3的能量损失。
注意，如果一棵植物与能量汇集机器连接的线段上没有植物，则能量损失为1。
现在要计算总的能量损失。
1 ≤ n, m ≤ 100,000。
所有我能独立做出来的数学题都是大水题
我们知道，令一个位置(a,b)到(0,0)之间的植物数量(如果包括(a,b)这棵植物的话)是f(a,b)
>令$r=gcd(a,b)$，$x=\frac{a}{r}$，$y=\frac{b}{r}$
那么$f(a,b)=\frac{a}{x}=\frac{b}{x}$
也就是$f(a,b)=\frac{a}{\frac{a}{r}}=r$
问题转化成求$\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}gcd(i,j)$
设$n \leq m$
套路推式子……
那么$ans=\sum\limits_{T=1}^{n} \lfloor \frac{n}{T} \rfloor \lfloor \frac{m}{T} \rfloor \sum\limits_{d|T} \frac{T}{d} \mu (d)$
令$g(n)=\sum\limits_{T=1}^{n} \sum\limits_{d|T} \frac{T}{d} \mu (d) = \sum\limits_{d=1}^{n} \mu (d) \sum\limits_{i=1}^{\frac{n}{d}}i$
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=1e5+7;
ll n,m,g[maxn];
char cc; ll ff;
template<typename T>void read(T& aa) {
aa=0;cc=getchar();ff=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
int prime[maxn],mu[maxn],totp;
bool ok[maxn];
void get_p() {
mu[1]=1;
For(i,2,n) {
if(!ok[i]) {
mu[i]=-1;
prime[++totp]=i;
}
For(j,1,totp) {
if(i*prime[j]>n) break;
ok[i*prime[j]]=1;
if(i%prime[j]) mu[i*prime[j]]=-mu[i];
else {
mu[i*prime[j]]=0;
break;
}
}
}
For(i,2,n) mu[i]+=mu[i-1];
}
ll get_g(ll n) {
if(~g[n]) return g[n];
ll rs=0;
for(ll i=1,j;i<=n;i=j+1) {
j=n/(n/i);
rs+=(mu[j]-mu[i-1])*(n/i)*(n/i+1)/2;
}
return g[n]=rs;
}
ll solve() {
ll rs=0;
for(ll i=1,j;i<=n;i=j+1) {
j=min(n/(n/i),m/(m/i));
rs+=(n/i)*(m/i)*(get_g(j)-get_g(i-1));
}
return rs;
}
int main() {
read(n); read(m);
if(n>m) swap(n,m);
get_p();
memset(g,-1,sizeof(g)); g[0]=0;
printf("%lld\n",2*solve()-n*m);
return 0;
}
bzoj4332 分零食
校长从幼儿园旁边的小吃店买了大量的零食决定分给同学们。
同学们依次排成了一列，其中有A位小朋友，有三个共同的欢乐系数O，S和U。如果有一位小朋友得到了x个糖果，那么她的欢乐程度就是$F(x)=O*x^2+S*x+U$。
现在校长开始分糖果了，一共有M个糖果。有些小朋友可能得不到糖果，对于那些得不到糖果的小朋友来说，欢乐程度就是1。
如果一位小朋友得不到糖果，那么在她身后的小朋友们也都得不到糖果。(即这一列得不到糖果的小朋友一定是最后的连续若干位)
求所有方案下小朋友欢乐程度乘积的总和对P取膜的结果
$M \leq 10000 , P \leq 255 , A \leq 10^8 , O \leq 4 , S \leq 300 , U \leq 100$
终于知道传说中的分治FFT是什么了，感觉什么多项式求逆，多项式……都是分治FFT呐
先给一个xxy大佬的题解的链接：https://www.cnblogs.com/TheRoadToTheGold/p/8960712.html
因为如果一位小朋友得不到糖果，那么在她身后的小朋友们也都得不到糖果。
所以设g[i][j] 表示前i位小朋友，分到j个糖果，且前i位小朋友都分到糖果的方案数
令F(x) 表示分到x个糖果的欢乐程度 ∴g[i][j] = ∑ g[i-1][j-k]*F(k)
记g[i]=g[i-1]*F，则 g[i]=F ^ i
但是要求的是 Σ g[i][m]
记f[n]=Σ g[i] i∈[1,n] ，那么ans=f[n][m]
f[n]=Σ g[i] i∈[1,n]
=Σ f(n/2)+Σ g[i] i∈[n/2+1,n]
=Σ f(n/2)+Σ F^i i∈[n/2+1,n]
=Σ f(n/2)+Σ F^(n/2+i) i∈[1,n/2]
=Σ f(n/2)+F^(n/2) * Σ F^i i∈[1,n/2]
=Σ f(n/2)+g(n/2)*f(n/2)
然后可以分治解决
如果n是奇数，f(n)=f(n-1)+g[n]=f(n-1)+g(n-1)*F
边界条件：g[][0]=1
//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const db PI=acos(-1),eps=1e-2;
const int maxn=(1<<17)+7;
ll n,m,len,mod;
char cc;ll ff;
template<typename T>void read(T& aa) {
aa=0;ff=1; cc=getchar();
while(cc!='-'&&(cc<'0'||cc>'9')) cc=getchar();
if(cc=='-') ff=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
aa*=ff;
}
struct Virt{
db r,i;
Virt(db r=0.0,db i=0.0) {this->r=r;this->i=i;}
Virt operator + (const Virt& b) const{return Virt(r+b.r,i+b.i);}
Virt operator - (const Virt& b) const{return Virt(r-b.r,i-b.i);}
Virt operator * (const Virt& b) const{return Virt(r*b.r-i*b.i,r*b.i+i*b.r);}
}F[maxn],f[maxn],g[maxn],X[maxn];
void Rader(Virt F[],ll len) {
for(int i=1,j=len>>1,k;i<len-1;++i) {
if(i<j) swap(F[i],F[j]);
k=len>>1;
while(j>=k) {j-=k;k>>=1;}
if(j<k) j+=k;
}
}
void FFT(Virt F[],ll len,ll on) {
Rader(F,len);
for(int h=2;h<=len;h<<=1) {
Virt wn=Virt(cos(-on*2*PI/h),sin(-on*2*PI/h));
for(int j=0;j<len;j+=h) {
Virt w=Virt(1,0);
for(int i=j;i<j+h/2;++i) {
Virt u=F[i],v=w*F[i+h/2];
F[i]=u+v;
F[i+h/2]=u-v;
w=w*wn;
}
}
}
if(on==-1) For(i,0,len) F[i].r/=len;
}
void debug() {
printf("g: "); For(i,0,m) printf("%lld ",(ll)g[i].r);printf("\n");
printf("f: "); For(i,0,m) printf("%lld ",(ll)f[i].r);printf("\n");
}
void get_mod() {
For(i,0,m) f[i].r=((ll)(f[i].r+eps))%mod,f[i].i=0;
For(i,0,m) g[i].r=((ll)(g[i].r+eps))%mod,g[i].i=0;
}
void solve(ll N) {
if(!N) {g[0].r=1;return;}
if(N&1) {
solve(N-1);
FFT(g,len,1);
For(i,0,len) g[i]=g[i]*F[i];
FFT(g,len,-1); For(i,m+1,len) f[i].r=f[i].i=g[i].r=g[i].i=0;
For(i,0,m) f[i]=f[i]+g[i];
}
else {
solve(N>>1);
For(i,0,m) X[i]=f[i];
FFT(X,len,1); FFT(g,len,1);
For(i,0,len) X[i]=X[i]*g[i];
For(i,0,len) g[i]=g[i]*g[i];
FFT(X,len,-1);FFT(g,len,-1);
For(i,m+1,len) X[i].r=X[i].i=g[i].r=g[i].i=0;
For(i,0,m) f[i]=f[i]+X[i];
}
get_mod();
// printf("solve %lld:\n",N); debug();
}
int main() {
ll x,y,z;
read(m); read(mod); read(n);
read(x); read(y); read(z);
For(i,1,m) F[i].r=((ll)x*i*i+y*i+z)%mod;
for(len=1;len<=(m<<1);len<<=1);
FFT(F,len,1);
solve(n);
printf("%lld\n",(ll)f[m].r);
return 0;
}
弱者就是会被欺负呀
浙公网安备 33010602011771号