2022ACTF-Crypto-impossible RSA

impossible RSA wp

0x01 题目源码

server.py

from Crypto.Util.number import *
from Crypto.PublicKey import RSA

e = 65537
flag = b'ACTF{...}'

while True:
    p = getPrime(1024)
    q = inverse(e, p)
    if not isPrime(q):
        continue
    n = p * q;
    public = RSA.construct((n, e))
    with open("public.pem", "wb") as file:
        file.write(public.exportKey('PEM'))
    with open("flag", "wb") as file:
        file.write(long_to_bytes(pow(bytes_to_long(flag), e, n)))
    break

public.pem

-----BEGIN PUBLIC KEY-----
MIIBITANBgkqhkiG9w0BAQEFAAOCAQ4AMIIBCQKCAQB+pWAiyLgiiDUmsUJs4sGi
BJeEwLvitqUvBVtcgPEFK4vO4G6CNAd3JlN8zBqJRBVn1FRlcxGPPXuJgIjMOkyV
G4vo3mLr/v/pER79JrPgP8E5hShao5rujsue8NUq9+r1dUsnqU3gEiPyZspAG+//
8P7TW0XcvCy5olRZqkV/QD6dlqjBaufWgTL2iMCtkadXT99ETmmgDVJ/GE51xErz
pE8poKXjJqnwZEWEjdcqO1RXHKLAcmm3mpQEGbFOXWlb2cqSnKTbtJ0cVQ93y3gA
mjCCBJrQLulx+5Oyn2+1rkRlHuMSq82DC0qAMvbc/DTjlTVYSC+GvIpEEFR344/5
AgMBAAE=
-----END PUBLIC KEY-----

bytes_to_long(flag)

8273086882440893360458062957389163084656045191542493618199369528956277216626884353986044368396198156428766254991928690583227149075264217246716715502497271453823598984519037301602775476502736840821942623288225980044817912940317041496675271105285924648202112216540495276381694590948153181922044287087121526235593090625653756288948499134042427779455887781328892794911088854654421379942237290840799205667104402295294924690771201447934282318850564703279100891083617354084345663030868007048086929831020873706613566948846194280096109248694845560054847526215721665897469865078997234299897107511688667705001432037926136840958

0x02 分析

\(\qquad\) 总览

\(\qquad\) 给了我们三个文件，1.公钥文件；2.密文；3.加密程序。前两个文件我们再熟悉不过了，通过公钥文件拿到 n ，解密时要拿到密文的整数类型（密文文件原本是字符文件）

\(\qquad\) 分段

• p = getPrime(1024)
  q = inverse(e, p)
  if not isPrime(q):
  	continue
  

  \(\qquad\) 这里出了 p 和 q 的值， p 的值是随机的我们不得而知，我们可以研究一下 q 的值，在给出的这个函数中我们可以得知一些数学关系：

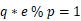  ，还可以修改一下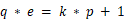： k为正整数，并且 q 是个素数。

0x03 decrypt

\(\qquad\) 整理

\(\qquad\) 我们整理一下我们已有的信息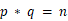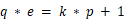： ， ，怎么将他们联系起来呢。

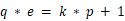
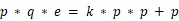
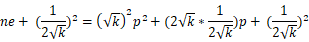
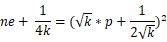
\(\qquad\) 到这里，是不是很明确了？其实整个程序最重要的部分已经分析完了，但是小数的计算并不方便，我们还需要再化简一下：

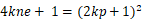
\(\qquad\) 我们都知道 gmpy2 的库中有一个函数 iroot() 可以帮助我们开方，我们只要遍历出 k 的值就可以解题啦，接下来的事情就交给脚本了。\(\qquad\)

\(\qquad\) 脚本

点击查看代码

from gmpy2 import *
from Crypto.Util.number import *
n = 15987576139341888788648863000534417640300610310400667285095951525208145689364599119023071414036901060746667790322978452082156680245315967027826237720608915093109552001033660867808508307569531484090109429319369422352192782126107818889717133951923616077943884651989622345435505428708807799081267551724239052569147921746342232280621533501263115148844736900422712305937266228809533549134349607212400851092005281865296850991469375578815615235030857047620950536534729591359236290249610371406300791107442098796128895918697534590865459421439398361818591924211607651747970679849262467894774012617335352887745475509155575074809

e = 65537

num = 2

ne = n * e
k = 1

with open('flag','rb')as f:
    c = f.read()
c = bytes_to_long(c)
while (True):
    num1 = 4 * k * ne + 1
    if (iroot(num1, 2)[1] == True):
        num2 = iroot(num1, 2)[0] - 1
        p = num2 // k // 2
        print('p = ', p, ' ', is_prime(p))
        break
    k += 1
q = n //p
d = invert(e,(p-1)*(q-1))
m = pow(c,d,n)
print(long_to_bytes(m))