CF1827C Palindrome Partition

CF1827C Palindrome Partition

前言

一个下午和 jimmywang 大力发明未果，写题解以记之。

思路

首先考虑求出以每个位置结尾的不可分割的偶回文串，这样就可以从前往后转移，但如果同一个位置结尾的这样的串有很多，\(\text{dp}\) 的复杂度肯定炸。

但其实每个点结尾的不可分割的偶回文串只有一个。

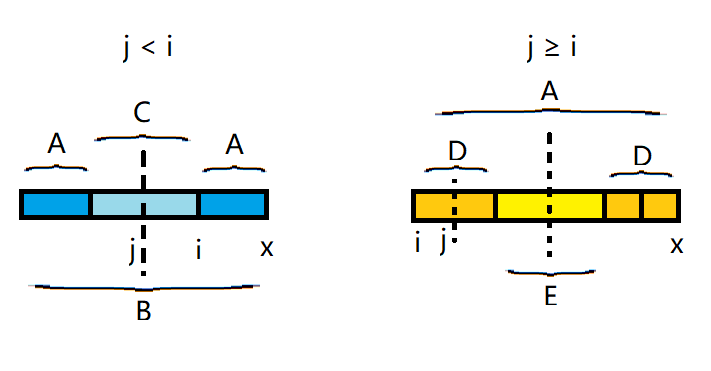
证明：假设以 \(x\) 这个位置结尾存在第二短的不可分割的偶回文串。记第一短的不可分割的偶回文串为 \(A\)，第二短的为 \(B\), \(A\) 的左端点为 \(i\)，\(B\) 的对称中心的左侧点为 \(j\)。若 \(j < i\)，那么 \(B\) 形如 \(A+C+A\)，其中 \(C\) 也为偶回文串，与 \(B\) 是不可分割的矛盾。若 \(j \ge i\)，则 \(A\) 形如 \(D+E+D\)，其中 \(D\) 与 \(E\) 都是偶回文串，与 \(A\) 是不可分割的矛盾。故 \(B\) 不存在，以 \(x\) 结尾的不可分割的偶回文串只有一个，且是以 \(x\) 结尾的最短的偶回文串。

可以结合图理解一下：

那么每个点只可能由前面的一个点转移过来，\(\text{dp}\) 的复杂度是 \(O(n)\) 的。

只需要在合适的复杂度里找出以每个点为结尾的最短偶回文串即可。

众所周知，\(\text{Manachar}\) 算法可以在线性时间内求解每个回文中心往外扩展的最长回文串。但我们要求的是最短。所以一个叫做车拉马的算法诞生了

先把所有对称中心以及每个中心当前对应期望回文串长度放进一个 \(\text{pair}\) 里入队，依然考虑从每个对称中心往外扩，如果当前期望长度下是回文串且右端点没被标记过，那就标记右端点，并把期望长度加 \(2\) 继续入队，否则直接出队。由于每个右端点只能被标记一次，复杂度 \(O(n)\)。

非常的对啊。

被轻松 \(\text{Hack}\) 了，例如在 \(\text{abbbba}\) 中，中间三个 \(\text{bb}\) 被标记完后就扩不到整个串了。

既然线性做不到，舍弃一点复杂度，多个 \(\log\) 也没事嘛。

把所有右端点扔进一个 \(\text{set}\) 里，表示未被标记的右端点的集合，每次入队前用 \(\text{upper_bound}\) 找到后面第一个没被标记右端点。

与之前不同的是，如果一个对称中心从队中取出，其原本期望长度对应的串是否为回文串用 \(\text{Hash}\) 判断。若不是则直接出队，否则当前右端点没被标记过就标记，并找到下一个右端点继续入队。

但写完以后又挂了，\(\text{Hack}\) 是 \(\text{abbbbaabbbba}\)。对，又是它。答案是 \(24\)，但输出是 \(23\)。原因是一个中心往下跳很远找到下一个右端点，并且赶在离那个右端点较近的中心之前把它标记了，就gg了。（上面这个串中最后一个 \(\text{a}\) 匹配了第一个 \(\text{a}\)）

一个普通队列倒下了，就有千万个优先队列站起来

按期望的回文串长度丢进优先队列（小根堆），复杂度 \(O(n \log n)\)。

真的吗？这个过程唯一的问题在于这一步：

否则当前右端点没被标记过就标记，并找到下一个右端点继续入队

如果一个中心每次出队没有标记任何右端点又被入队，相当于它被虚空入队很多次，是否会使复杂度不是 \(O(n \log n)\) 呢？

暂时还不太会证，但是能过，只能感性理解所有中心一轮出入队必然能标记一些右端点，出队时期望右端点已被标记的情况数不会很多。

因为复杂度证不出来，jimmywang 觉得没有前途，改造了原版 \(\text{Manachar}\)，严格 \(O(n \log n)\)。

后来发现 jimmywang 的方法在题解区有用链表实现 \(O(n)\) 的。

Code

点击查看代码

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define mpr make_pair
const ll SIZE = 500005;
const ll mod = 180181327;
ll T, n;
char ch[SIZE];
ll las[SIZE];
ll dp[SIZE];
ll sum[SIZE], sum1[SIZE];
ll pp[SIZE];

inline ll rd(){
	ll x = 0, f = 1;
	char ch = getchar();
	while(ch < '0' || ch > '9'){
		if(ch == '-') f = -1;
		ch = getchar();
	}
	while(ch >= '0' && ch <= '9'){
		x = (x<<1) + (x<<3) + (ch^48);
		ch = getchar();
	}
	return x*f;
}

ll power(ll x, ll y){
	ll jl = 1;
	while(y){
		if(y & 1) jl = (jl * x) % mod;
		x = (x * x) % mod;
		y >>= 1;
	}
	return jl;
}

bool check(ll l, ll r){
	if(l < 1 || r > n) return false;
	if(l % 2 == r % 2) return false;
	ll mid = (l + r) / 2;
	ll x = (sum[mid] - ((sum[l-1] * pp[mid-l+1]) % mod) + mod) % mod;
	ll y = (sum1[mid+1] - ((sum1[r+1] * pp[mid-l+1]) % mod) + mod) % mod;
	return (x==y);
}

int main(){
	T = rd(); priority_queue<pair<ll, ll> > q; set<ll> s;
	pp[0] = 1;
	for(ll i = 1; i <= 500000; i++) pp[i] = (pp[i-1] * 26) % mod; 
	while(T--){
		n = rd(); cin >> ch+1;
		sum[0] = sum1[n+1] = 0; 
		s.clear();
		for(ll i = 1; i <= n; i++){
			sum[i] = ((sum[i-1] * 26) % mod + ch[i] - 'a') % mod;
		}
		for(ll i = n; i >= 1; i--){
			sum1[i] = ((sum1[i+1] * 26) % mod + ch[i] - 'a') % mod;
		}
		for(ll i = 1; i <= n; i++) las[i] = -1, s.insert(i);
		for(ll i = 1; i <= n; i++) q.push(mpr(-1, i));
		while(q.size()){
			ll x = q.top().second, len = -q.top().first; q.pop();
			if(x-len+1 < 1 || x+len > n) continue;
			if(ch[x-len+1] != ch[x+len]) continue;
			if(las[x+len] == -1){
				las[x+len] = x-len;
				s.erase(x+len);
			}
			if(s.upper_bound(x) != s.end()){
				ll jl = *s.upper_bound(x);
				if(check(x-(jl-x)+1, jl)) q.push(mpr(-(jl-x), x));
			}
		}
		ll ans = 0;
		for(ll i = 1; i <= n; i++){
			if(las[i] != -1){
				dp[i] = dp[las[i]] + 1, ans += dp[i];		
			}
			else dp[i] = 0;
		}
		printf("%lld\n", ans);
	}
	return 0;
}