P5392 [Cnoi2019]雪松树之约

P5392 [Cnoi2019]雪松树之约

首先分析一下给出的图的形态，限制 \(1\) 表示每相邻两层之间对应点之间两两连边，限制 \(2\) 和限制 \(3\) 表示每一层是一个环，所以整张图可以形象地看成是由 \(L\) 个大小为 \(x\) 的环上下顺次相连形成的柱状图。

观察数据范围，\(L\) 很大但 \(x\) 很小，所以可以考虑对每一层做状态压缩，然后利用矩阵快速幂进行层与层之间的转移。对每个环逆时针编号为 \(1 \sim x\)，设 \(s_i\) 表示第 \(i\) 层的状态，\(s_i\) 二进制下低位开始第 \(j\) 位为 \(1\) 或 \(0\) 表示环上编号为 \(j\) 的点选或不选。

先预处理出每层满足独立集的状态，发现当 \(x=17\) 时，一共有 \(3571\) 种。如果用这些状态转移在矩阵乘法自带的 \(O(n^3)\) 复杂度下根本无法通过。那么能否再压缩掉一些状态？

手动模拟发现有些情况其实是本质相同的。

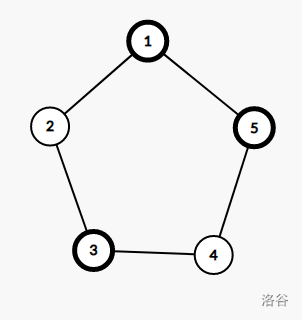
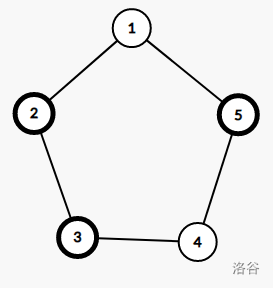
例如上面两个环，忽略编号时，右图中的环可由左图中的环逆时针旋转 \(144^{\circ}\) 得到，也就是说，这两个环实际上是本质相同的。

考虑合并这种旋转以后能重合的本质相同的环，再跑一遍发现可用状态只剩下 \(211\) 种，算一下复杂度，似乎只要常数小刚好能过？

然后想压缩掉这些本质相同的状态后如何转移。对于一些本质相同的状态，我们从中选出其中一个作为这些状态的代表环，而这个代表环是有编号对应的。我们设 \(dp_{i,s_j}\) 表示第 \(i\) 层的状态为 \(s_j\) 且固定第 \(i\) 层不动的方案数。这里不动的含义是当前层选的状态与该状态对应的代表环严格相同，而第 \(1\) 到 \(i-1\) 层可整体旋转与之相匹配。当从 \(dp_{i-1,s_k}\) 向 \(dp_{i,s_j}\) 转移时，记状态 \(s_k\) 通过旋转得到的 \(x\) 个状态中，与 \(s_j\) 构成独立集的状态数有 \(cnt_{k,j}\) 种。那么有如下转移：

\[dp_{i,s_j}=\sum dp_{i-1,s_k}\times cnt_{k,j} \]

转化为矩阵，容易发现 \(cnt\) 数组即为转移矩阵。

最后统计答案时，对于第 \(L\) 层的每一种状态的答案，要乘上该状态里旋转可得的状态个数。（相当于将整张图旋转一定的角度）

注意常数，尽量减少取模，时间复杂度 \(O(x \cdot 2^x + 211^3 \cdot \log L)\)

点击查看代码

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const ll SIZE = 200005;
const ll mod = 998244353;
ll L, n;
bool mp[150005];
bool mp1[150005];
ll cntm[150005];
ll a[SIZE], id[150005], tot;

inline ll rd(){
	ll f = 1, x = 0;
	char ch = getchar();
	while(ch < '0' || ch > '9'){
		if(ch == '-') f = -1;
		ch = getchar();
	}
	while(ch >= '0' && ch <= '9'){
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return f*x;
}

struct node{
	ll o[212][212];
}zy;

node jl;
node mul(node A, node B){
	for(int i = 0; i <= tot; i++)
		for(int j = 0; j <= tot; j++){
			jl.o[i][j] = 0;
			for(ll k = 0; k <= tot; k++){
				jl.o[i][j] += A.o[i][k] * B.o[k][j] % mod;
			}
			jl.o[i][j] %= mod;
		}
	return jl;	
}

node power(node x, ll y){
	node j2;
	for(int i = 0; i <= tot; i++)
		for(int j = 0; j <= tot; j++)
			j2.o[i][j] = (i==j);
	while(y){
		if(y & 1) j2 = mul(j2, x);
		x = mul(x, x);
		y >>= 1;
	}
	return j2;
}

int main(){
	L = rd(), n = rd();
	for(int i = 0; i < (1<<n); i++){
		ll now = i; bool ff = 0;
		for(ll j = 2; j <= n; j++){
			if((i&(1<<(j-1))) && (i&(1<<(j-2)))){
				ff = 1;
				break;
			}
		}
		if((i&1) && (i&(1<<(n-1)))) ff = 1;
		if(!ff){ //同一个环内满足两两不相邻
			for(ll j = 1; j < n; j++){
				now = ((now&1)<<(n-1))|(now>>1);
				if(mp[now]){
					cntm[id[now]]++;//更新循环意义下相同方案的个数
					ff = 1;
					break;
				}
			}
		}
		if(!ff){//出现一种新的本质不同的环
			cntm[tot+1] = 1; 
			mp[i] = 1;
			a[++tot] = i;
			id[a[tot]] = tot;
		}
	}	
	for(int i = 1; i <= tot; i++){//枚举可能的转移，构造转移矩阵
		for(int j = 1; j <= tot; j++){
			if((a[i]&a[j]) == 0) zy.o[i][j]++;	
			if(a[i] == 0) continue;
			ll now = a[i], st = a[i]; bool ff = 0;
			for(int h = 1; h < n; h++){
				now = ((now&1)<<(n-1))|(now>>1);
				if(ff && now == st) break;
				if((now&a[j]) == 0) zy.o[i][j]++;
				ff = 1;
			}
		}
	}
	node ans = power(zy, L-1);
	ll aans = 0;
	for(int i = 1; i <= tot; i++){
		ll jl = 0;
		for(int j = 1; j <= tot; j++){
			jl = jl + ans.o[j][i];
			if(jl >= mod) jl -= mod;
		}
		jl = jl * cntm[i] % mod; //统计最顶层为状态i的方案数 
		aans = aans + jl;
		if(aans >= mod) aans -= mod;
	}
	printf("%lld", aans);
	return 0;
}