2016 ACM/ICPC Asia Regional Qingdao Online(SDKD 2024 Summer Training Contest H2)
A - I Count Two Three
题意
给定\(n\),求第一个\(\ge n\)的数\(k\),且\(k=2^a3^b5^c7^d\)。
思路
考虑到样例很多,直接打表存入set省去数组排序操作,由于\(n\le 10^9\),所以只需要打到\(10^9\)后二分即可。(记得加上快读快写,T得饱饱的😭💔)
代码
点击查看代码
#define _CRT_SECURE_NO_WARNINGS
#include<bits/stdc++.h>
using namespace std;
#define int long long
int read() {
int x = 0, f = 1;
char c = getchar();
while (c < '0' || c>'9') { if (c == '-') f = -1; c = getchar(); }
while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return x * f;
}
void write(int x) {
if (x == 0) {
putchar('0'); return;
}
if (x < 0) putchar('-'), x = -x;
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
set<int> s;
int A[40], B[40], C[40], D[40];
void init()
{
A[0] = B[0] = C[0] = D[0] = 1;
for (int a = 1; a < 30; a++)
{
A[a] = A[a - 1] * 2;
}
for (int b = 1; b < 19; b++)
{
B[b] = B[b - 1] * 3;
}
for (int c = 1; c < 13; c++)
{
C[c] = C[c - 1] * 5;
}
for (int d = 1; d < 11; d++)
{
D[d] = D[d - 1] * 7;
}
for (int a = 0; a < 30; a++)
{
int t1 = A[a];
for (int b = 0; b < 19; b++)
{
int t2 = t1 * B[b];
if (t2 > 1e9 || t2 < 0)
{
break;
}
for (int c = 0; c < 13; c++)
{
int t3 = t2 * C[c];
if (t3 > 1e9 || t3 < 0)
{
break;
}
for (int d = 0; d < 11; d++)
{
int t4 = t3 * D[d];
if (t4 > 1e9 || t4 < 0)
{
break;
}
s.insert(t4);
}
}
}
}
}
void solve()
{
int n = read();
write(*s.lower_bound(n));
putchar('\n');
}
signed main()
{
init();
int T = read();
while (T--)
{
solve();
}
return 0;
}
B - Cure
题意
给定\(n\),求\(\sum_{k=1}^n\frac1{k^2}\),结果四舍五入,精确到小数点后5位。
思路
也是打表,但开大了数组会爆,考虑到\(\frac1{k^2}\)越往后越小,而只要求精确到小数点后5位,所以可以取n$\ge$1e6以后就等于\(10^6\)时的值。
代码
点击查看代码
#define _CRT_SECURE_NO_WARNINGS
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef pair<int, int> pii;
const int mxn = 1e6 + 5;
double f[mxn];
void init()
{
double sum = 0.0;
for (int i = 1; i <= 1e6; i++)
{
sum += (double)(1.0 / (double)(i * i));
f[i] = sum;
}
}
void solve()
{
init();
int n;
while (scanf("%lld", &n) != EOF)
{
if (n >= 1000000)
{
printf("%.5lf\n", f[1000000]);
}
else
{
printf("%.5lf\n", f[n]);
}
}
}
signed main()
{
int T = 1;
//scanf("%lld", &T);
while (T--)
{
solve();
}
return 0;
}
D - Tea
题意
壶里有\([L,R](L \le R)\)的水,倒俩杯里,倒完时俩杯里水相差不超过\(1\),壶里最多可以余\(1\),求最少多少次一定能倒完。
思路
由于\(L \le R\),显然当\(R\le 1\),壶里的水相差不超过1,不用倒;\(R=2\),只用往任意一个杯里倒1单位的水即可;当\(L=R或L=R-1\),只需分别向两个杯里倒L单位的水;其他情况,第一次倒给甲\(L/2+0.5,第二次倒给乙L/2+1.5,再给甲倒L/2+2.5,再给乙倒L/2+3.5···得(R - L)/2+1\)。
代码
点击查看代码
#define _CRT_SECURE_NO_WARNINGS
#include<bits/stdc++.h>
using namespace std;
#define int long long
void solve()
{
int L, R;
while (scanf("%lld%lld", &L, &R) != EOF)
{
if (!L) // L = 0 与 L = 1 等效(因为壶内可留1升水)
{
L++;
}
if (R <= 1)
{
putchar('0');
}
else if (R == 2)
{
putchar('1');
}
else if (L == R || L == R - 1)
{
putchar('2');
}
else
{
printf("%lld", (R - L) / 2 + 1);
}
putchar('\n');
}
}
signed main()
{
int T = 1;
//scanf("%lld", &T);
while (T--)
{
solve();
}
return 0;
}
E - Balanced Game
题意
相较于传统石头剪子布游戏的\(3\)种形状,现在给定\(n\)种形状,问游戏是否平衡(即随机选择形状,赢的可能性正好是\(50%\),无论对方如何选择,如果平局,继续游戏直到有人获胜)。
思路
对于n种形状,假设\(n\)个人玩,那么每个人都要打败\(\frac{n-1}2\)的人,又要被\(\frac{n-1}2\)的人打败,则当n是奇数的时候(整除)游戏平衡。
代码
点击查看代码
#define _CRT_SECURE_NO_WARNINGS
#include<bits/stdc++.h>
using namespace std;
void solve()
{
int n;
scanf("%d", &n);
if (n & 1)
{
printf("Balanced\n");
}
else
{
printf("Bad\n");
}
}
signed main()
{
int T = 1;
scanf("%d", &T);
while (T--)
{
solve();
}
return 0;
}
F - The Best Path
题意
\(n\)个点,\(m\)条边(可能有自环),问能否构成欧拉路径(通路或回路),如果能,求点权异或和的最大值。
思路
如果能构成,通路则只有一条路径;回路则需要枚举起点,如果经过点\(a\)偶数次则不需要异或(\(w_a\)^\(w_a = 0\))。由于通路中起点和终点的度数为奇数,所以取值应该向上取整;回路则通过起点的次数要多通路一次,终点的次数相同。
代码
点击查看代码
#define _CRT_SECURE_NO_WARNINGS
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mxn = 1e6 + 5;
int degree[mxn], point[mxn];
void solve()
{
int n , m ;
cin >> n >> m;
fill(degree, degree + n + 1, 0);
for (int i = 1; i <= n; ++i)
{
cin >> point[i];
}
for (int i = 1; i <= m; ++i)
{
int u , v ;
cin >> u >> v;
degree[u]++;
degree[v]++;
}
int cnt = 0;
for (int i = 1; i <= n; ++i)
{
if (degree[i] % 2)
{
cnt++;
}
}
if (cnt > 2)
{
cout << "Impossible" << endl;
return;
}
int ans = 0;
for (int i = 1; i <= n; ++i)
{
if ((degree[i] + 1) / 2 % 2)
{
ans ^= point[i];
}
}
if (!cnt)
{
for (int i = 1; i <= n; ++i)
{
ans = max(ans, ans ^ point[i]);
}
}
cout << ans << endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T;
cin >> T;
while (T--)
{
solve();
}
return 0;
}
G - Sort
题意
\(n\)个有序序列,第i个序列有\(a_i\)个元素,每次选择至多\(k\)个序列合并,使得最后只有\(1\)个序列,合并代价为这些序列的长度和,总代价不能超过\(T\)。求\(k\)的最小值。
思路
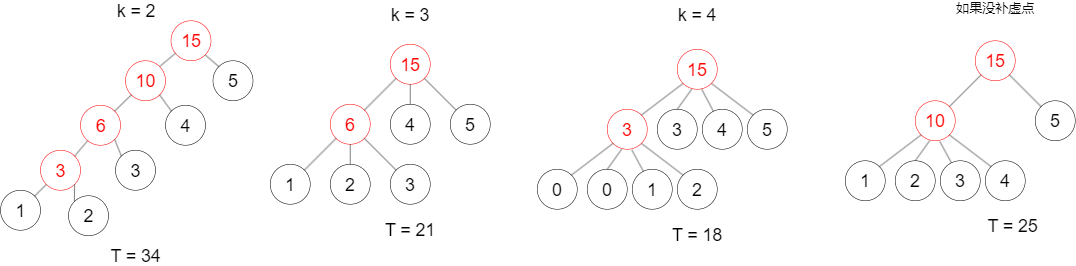
\(k\)越大,代价越小,有了单调性就二分\(k\),每次都取前\(k\)小的序列合并后再合并,此时的代价最小,但是注意,对于每个\(k\),总共需要合并\(n-1\)个数,每次合并了\(k-1\)个数,如果\((n-1)\)%\((k-1)\)!=\(0\),就凑不够 k 个,凑不够这几个一定是先合并才能保证代价最小,所以可以用权为0的虚点凑够k个,本质是一个\(k\)叉哈夫曼树。然后
就超时了,用两个普通队列代替优先队列,一个存原数组,另一个存合并后的数,显然两个队列都可以保证是有序的,取的时候比较取最小值即可,从而将时间复杂度从\(O(n*\log n*\log n)优化到O(n*\log n)\)。
代码
点击查看代码
#define _CRT_SECURE_NO_WARNINGS
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n, t;
vector<int> v;
bool check(int k)
{
queue<int> p, q; // 插入时有序,所以可以代替优先队列
for (int i = 0; i < n; i++)
{
p.push(v[i]);
}
int res = 0, cnt = 0;
if ((n - 1) % (k - 1))
{
cnt = (n - 1) % (k - 1) + 1; // 虚点数量就是(k - cnt)
int sum = 0;
for (int i = 0; i < cnt; i++)
{
sum += p.front();
p.pop();
}
q.push(sum);
res += sum;
}
while (p.size())
{
int sum = 0;
for (int i = 0; i < k; i++) // 前k小
{
if (p.size() && q.size())
{
if (p.front() <= q.front())
{
sum += p.front();
p.pop();
}
else
{
sum += q.front();
q.pop();
}
}
else if (p.empty())
{
sum += q.front();
q.pop();
}
else if (q.empty())
{
sum += p.front();
p.pop();
}
}
res += sum;
q.push(sum);
}
if (res > t) // 代价大了,说明k太小了
{
return true;
}
int sum = 0;
cnt = 0;
while (q.size() > 1)
{
sum += q.front();
q.pop();
cnt++;
if (cnt == k)
{
q.push(sum);
res += sum;
sum = cnt = 0;
}
}
if (res > t)
{
return true;
}
return false;
}
void solve()
{
cin >> n >> t;
v.resize(n);
for (int i = 0; i < n; i++)
{
cin >> v[i];
}
sort(v.begin(), v.end());
int l = 2, r = n, ans = 0;
while (l <= r)
{
int mid = (l + r) >> 1;
if (check(mid))
{
l = mid + 1;
}
else
{
ans = mid;
r = mid - 1;
}
}
cout << ans << endl;
v.clear();
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T = 1;
cin >> T;
while (T--)
{
solve();
}
return 0;
}
疑问
为什么这次用cin比scanf快多了😡?甚至比快读快写还快。是杭电OJ的问题吗,真给我T的饱了💔。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号