主席树学习笔记

可持久化线段树，以求区间第k小为应用举例。其实区间第k小是权值线段树、可持久化线段树与前缀和的综合应用，奈何中者的基础应用过于鸡肋，懒得从那开始学。

考虑区间第k与与可持久化线段树的适配。
先离散化，开桶。
第\(i\)棵线段树的所有叶子结点，是储存了原序列\([1,i]\)区间所有值的一列桶；树上的任意一个结点，其涵盖区间为\([l,r]\)，储存了原序列\([1,i]\)区间内（离散化后的）值域为\([l,r]\)的值的数量：即，一棵权值线段树。
由是可以发现，第\(i\)棵线段树相对于第\(i-1\)棵，由于总的要管的区间只大了一格，所以其相对于后者有变动的桶只有一个\(a[i]\),再回溯到根，所有有变动的结点形成了自根到叶的一条链。所以这玩意可以用可持久化线段树维护。
那么应当如何维护呢？

inline void modify(const int &x,int k,int pre,int l,int r){
	while(1){
		tr[k].sum=tr[pre].sum+1;
		if(l==r) break;
		const int mid=l+r>>1;
		if(x<=mid)
			tr[k].rs=tr[pre].rs,k=tr[k].ls=++tot_node,pre=tr[pre].ls,r=mid;
		else
			tr[k].ls=tr[pre].ls,k=tr[k].rs=++tot_node,pre=tr[pre].rs,l=mid+1;
	}
}

\(k\)是第\(i\)棵树的当前结点，\(pre\)是第\(i-1\)棵树的对应结点。
没有必要建空树。

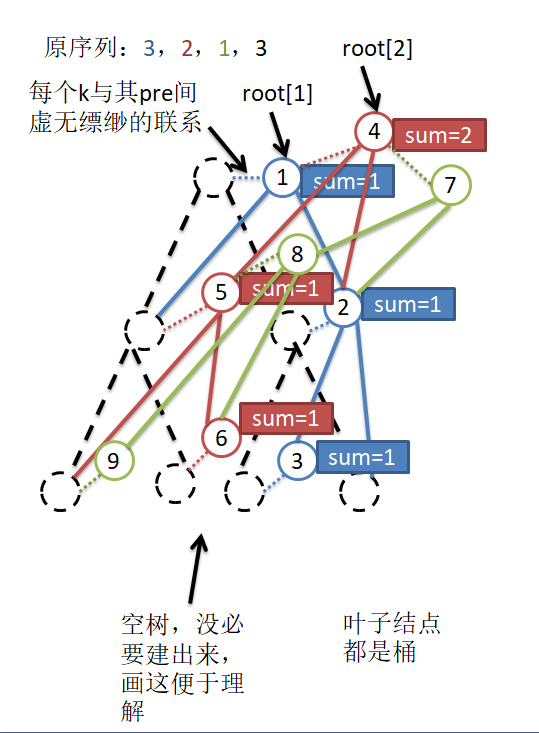
对着图理解一下，就是序列每扩张一位，就需要一棵新树，该树可以在上一棵树的基础上建，需要变动的只是modify()中递归的那一条链。反正最后我们要的就是这\(n\)棵权值线段树。

好了现在我们有\(n\)棵权值线段树了，那么该如何查询呢？

inline int query(int lt,int rt,int l,int r,int k){
	while(l<r){
		const int mid=l+r>>1,tot=tr[tr[rt].ls].sum-tr[tr[lt].ls].sum;
		if(tot<k)
			lt=tr[lt].rs,rt=tr[rt].rs,l=mid+1,k-=tot;
		else
			lt=tr[lt].ls,rt=tr[rt].ls,r=mid;
	}
	return l;
}

	int l=read(),r=read(),rk=read();
	cout<<sort_a[T.query(T.root[l-1],T.root[r],1,max_bucket,rk)]<<endl;

利用前缀和的思想，拿出第\(r\)和\(l-1\)棵线段树，只考虑它们每个对应同位结点\(sum\)之差，我们相当于就有了一棵只表示\([l,r]\)区间的权值线段树。于是问题就变成了“已知某原序列区间内任意一段值区间所涵盖的\(a_i\)个数，求区间第\(k\)小。易如反掌
往小了走，若行就进去；若不行就换大的，还把\(k-=tot\)。