【算法设计与分析】动态规划

 

---

1. 斐波那契数列

 

 

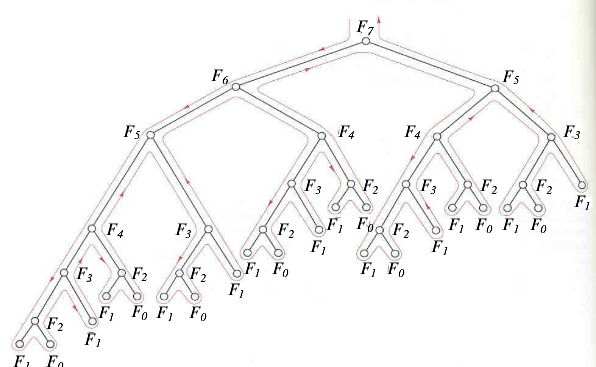
 显然，如果我们打算直接递归计算它的每个值，会有重复计算的部分，这个时候我们可以考虑把得到的值存起来，每次调用。

 首先，会自然的想到用数组存下，每次计算下标的前两位的值。

 

 

 

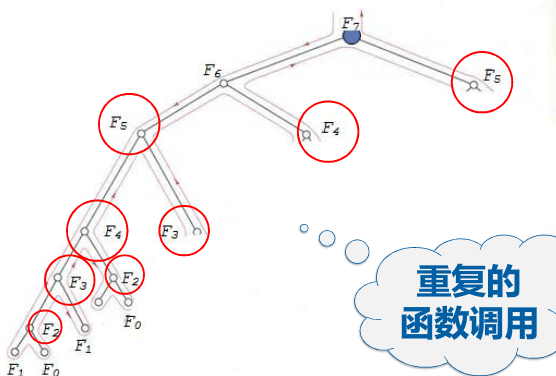
 但是，注意到，因为仍然是递归的形式，依然有重复的调用。

 这时，我们可以转变思维。不再使用自顶向下，而是使用自底向上，递推的想法。

其实每次都只需要保留最后两个数的值就能计算出下一个数的值了。这样减少了存储空间的占用。

 

 

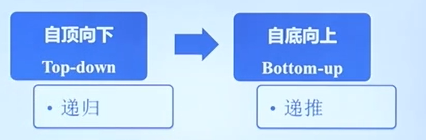
 从这里可以看出，分治和动态规划的差别，出发点是有重复的子问题。

我们可以使用分治递归的思想定下最优解的框架，但是实现时用动态规划，先把每个小问题解决，得到最优解，再递推地自底向上。

2.计算矩阵连乘

---

 

矩阵乘法的次数跟其N、M有关，所以我们要找到的是最适合的剧本连乘情况。

通过切分的方法，也就是使用括号，把四个乘法切分为不同的小问题。

 

 

 

 

 

 

 

 

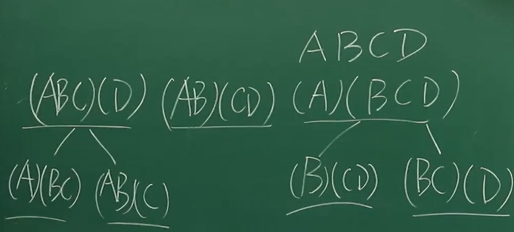
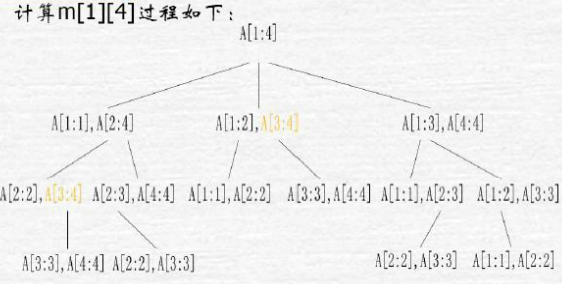
随后我们可以发现，要解决的中等拆分问题，可由更小的拆分问题解决，同时它可能出现多次。

类似这样的问题，就可以使用保存值之后直接调用的方法。

 

 

 

 

 

 大问题就变成了切割的左边小问题乘法次数+右边小问题乘法次数+两个相乘的次数

所以，接下来的问题是，如何设计存储？

 

 

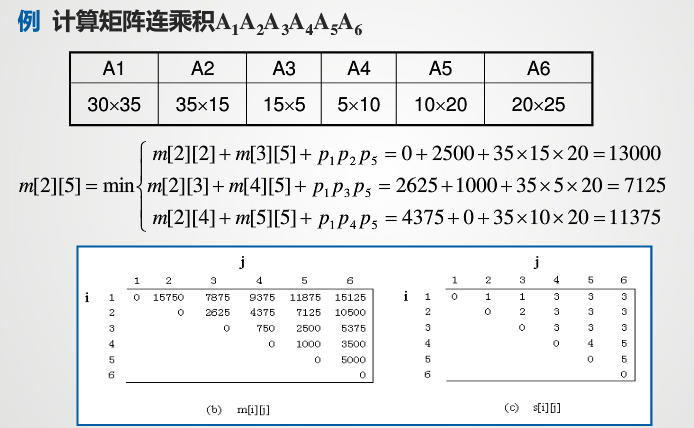
当我们计算m[2][5]时，有三种切割方式，左边[2][2]/[2][3]/[2][4],每一种又对应着其右边的[3][5]/[4][5]/[5][5]，最后加上左右两个新矩阵相乘的次数，我们在这三种方法中取最小；

要计算[3][5]我们也有[3][3],[4,5]  /  [3,4],[5]，我们在这两种方法中取最小；

要计算[4][5]我们需要计算[4] [4]，[5][5]，已无法再拆分，到达边界了，直接为0；

这里也可以看到，我们需要先设置一个边界，让递归有入口和出口，在这道题中，我们使主对角线的元素都为0；

经过刚才的分析，我们知道，我们的计算方式，是斜对角线向上进行的，这样才能计算出非相邻的两个元素的乘法结果；

 

 

 3. 最优二叉查找树

---

 

   3.1 来源

 

    如今在输入栏上输入关键字，搜索引擎都会按照以前搜索的关键字记录计算频率，得到用户最有可能想要的输入内容。

    如何高效查找带频率的键值，使频率高的值尽可能离根结点近，低的尽量远。

 

   3.2 核心

 

    二叉查找树： 左子树的任意结点都小于根节点，右子树的任意结点都大于根节点。

                          采用中根遍历一棵二叉查找树，可以得到树中关键字由小到大的序列。

                          二叉查找树中搜索一个关键字需要访问的结点数等于包含关键字的结点的深度加1。

 

    哈夫曼树：在数据通信中，需要将传送的文字转换成二进制的字符串，用0，1码的不同排列来表示字符。

                      在设计编码时，让使用频率高的用短码，使用频率低的用长码，以优化整个报文编码。

                      是最优二叉树，是一种带权路径长度最短的二叉树。

                      树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的 路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。

                       https://baijiahao.baidu.com/s?id=1663514710675419737&wfr=spider&for=pc这篇文章讲的很好

    区分两个概念，哈夫曼树的左右子树彼此没有关系，更关注频率值，而二叉查找树除了要尽量使频率高的离根近，还需要维持左右子树的大小顺序，保证键值的查找效率。

 

    所谓最优，是最少的平均比较次数。即

 

 

   3.3 参考资料

    https://www.cnblogs.com/henuliulei/p/10074216.html

    https://blog.csdn.net/tengweitw/article/details/16972241

    https://blog.csdn.net/liufeng_king/article/details/8694652

   3.4 理解

   由动态规划的思想，当T(i,j)min时，T（left）和T（right）也应该是最小的

   而C(i,j)=查找根结点+查找左子树+查找右子树