【算法设计与分析】时空权衡

0.起源

---

 

  最开始，我们会将一些常用的结果存储起来做表，进行预存储

  或者，我们会先对问题的部分或整体进行预处理。

 

1.具有此思想的算法

 

2.计数法排序，每趟计算小于本数的个数 

---

 

 

 

 

//注意else的内容，这样就可以每次都从i+1开始遍历

 

 

 

 

 

 比较操作：

 

 

 

 这种思想适合计算分布函数的频率

 

 

3.字符串匹配问题

---

 

首先，尝试列出几种可能的字符串匹配情况

设文本长度为n，模式长度为m

 

 【文本】This is a simple example

 【模式】example

 

 【文本】This is a simple example

 【模式】isa

 

 【文本】This is a simple example

 【模式】simpuuuu

 

【文本】This is a simple example

 【模式】ashuhasd

 

>>   如果我们使用暴力方法，那么我们为文本和模式设置头指针，都是正序比较，如果头指针不匹配，文本头指针往前走，如果匹配，文本和模式的头指针都往前走。

   这样我们在最坏的情况下，需要比较n-m+1次，而每次都需要比较m次，性能为O(mn);

   不过，对于自然语言文本，他的平均效率是O(n+m)

 

  为了减少比较次数，我们经过观察可以发现，即使前面的字符都匹配，只要最后一个不匹配，那么这次匹配就是失败的，那么，我们不妨换个角度，

  文本正序遍历， 而模式倒序遍历。

 

【文本】This is a simple example 

【模式】example

T

h

i

s

i

s

a

s

i

m

p

l

e

e

x

a

m

p

l

e

e

x

a

m

p

l

e

  

经过尝试，我们可以发现，文本尾部的S在模式中没有，我们可以直接移动到下面的位置，

 

T

h

i

s

i

s

a

s

i

m

p

l

e

e

x

a

m

p

l

e

e

x

a

m

p

l

e

此时虽然不匹配，但是文本尾部的p在模式中是存在的，不能排除把p对齐了之后匹配成功的情况

 

T

h

i

s

i

s

a

s

i

m

p

l

e

e

x

a

m

p

l

e

e

x

a

m

p

l

e

 

再一次出现了匹配失败的情况,但是文本尾部在模式的非尾部出现

 

T

h

i

s

i

s

a

s

i

m

p

l

e

e

x

a

m

p

l

e

e

x

a

m

p

l

e

这一次和第二次类似，尾部不匹配，但是在模式内出现，我们直接移动到相对的位置

 

T

h

i

s

i

s

a

s

i

m

p

l

e

e

x

a

m

p

l

e

e

x

a

m

p

l

e

匹配成功!

 

 【文本】This is a simple example

 【模式】isa

 

【文本】This is a simple example

 【模式】simpuuuu

 

【文本】This is a simple example

 【模式】ashuhasd

 

同理，这些模式也可以如此匹配。

 

接下来，我们看看教材Horspoor算法，思考有没有遗漏的情况

 

情况1，文本的尾部不匹配，同时也不在文本中，那么我们可以直接移动模式的距离。

 

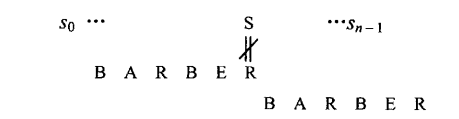
 情况2：文本尾部不匹配，模式内存在这个字符，但是，此时可能有多个字符相等。这种情况是我们没考虑的，那么，我们应该匹配哪个字符呢？

            我们是从尾部开始匹配模式的，如果直接从模式的正序第一个，直接移动，那么会漏比掉模式倒序的第一个

             所以，我们应该让模式的倒序第一个相等的字符和文本尾部归位

 

 

 

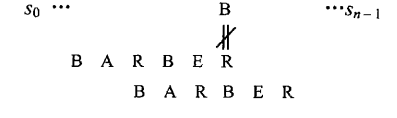
情况3:我们刚刚出现了这种情况，倒序匹配了部分，不匹配的字符不在模式中，直接移动模式的长度

 

 

 

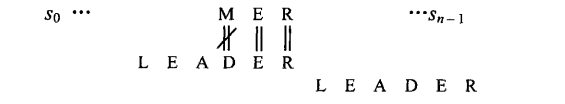
 情况4:出现不匹配情况，但是尾部R是模式的尾部，同时R在模式中出现了多次，那么此时应该把模式中前m-1个字符串中的R和文本的R对应

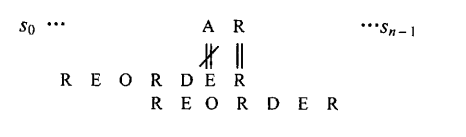
 而Boyer-Moore算法与其在有部分匹配的情况是不同处理的