前缀和&差分

前缀和&差分（蒟蒻篇）

前缀和

前缀和是指某序列的前n项和，而差分可以看成前缀和的逆运算。
一般用于大量的求一段连续区间的和
时间复杂度：预处理O(n),查询O(1)

一维前缀和

模板

作用是：找a序列的一段连续区间的和

for(int i=1;i<=n;i++)
        sum[i]=sum[i-1]+a[i];
        
    a序列l~r的和 = sum[r]-sum[l-1]

原理

sum[1] = a[1]
sum[2] = sum[1] + a[2] = a[1] + a[2]
sum[5] = sum[4] + a[5] = a[1] + a[2] + a[3] + a[4] + a[5]
sum[n] = sum[n-1] + a[n] = a[1] + .... + a[n]
所以 l ~ r 的和 = a[l] + .... + a[r] = sum[r] - sum[l-1]

来个模板题练练手 一维前缀和

二维前缀和

顾名思义，二位前缀和解决的就是二维数组的问题

模板

作用是：找a序列的一块连续区间的和

for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++)
            sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j];
    }
    x1 ~x2, y1 ~y2整个区域的和
    S[x1 ~ x2][y1 ~ y2] = sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1]

原理

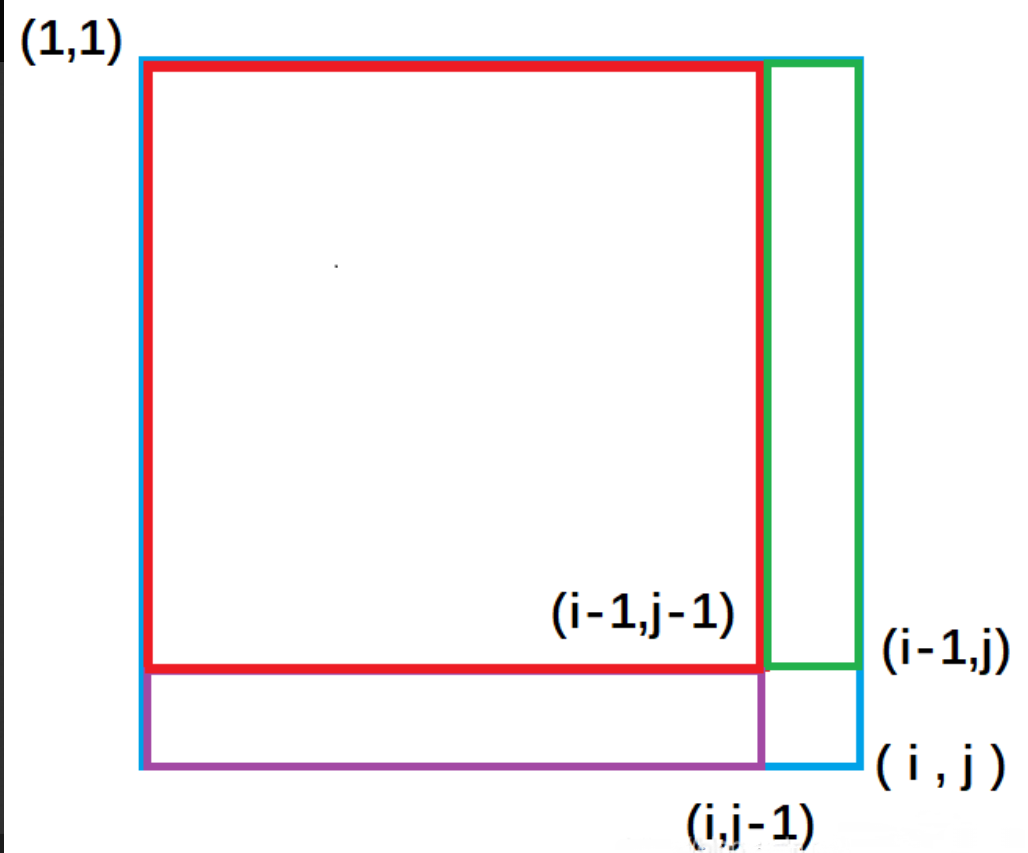
紫色面积是指(1,1)左上角到(i,j-1)右下角的矩形面积, 绿色面积是指(1,1)左上角到(i-1, j )右下角的矩形面积。每一个颜色的矩形面积都代表了它所包围元素的和。

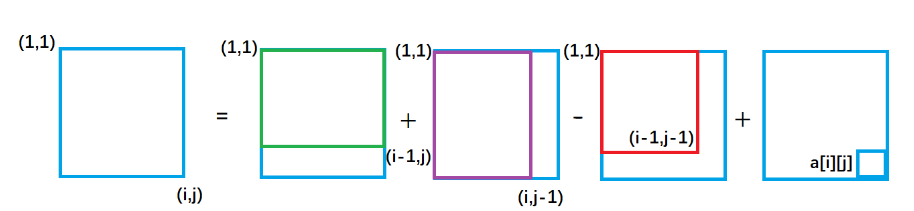
二位前缀和预处理

s[i][j] = s[i-1][j]+s[i][j-1]+a[i][j]-s[i-1][j-1]

去求以(x1,y1)为左上角和以(x2,y2)为右下角的矩阵的元素的和

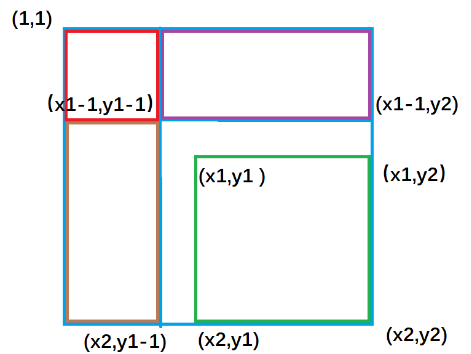
紫色面积是指 ( 1,1 )左上角到(x1-1,y2)右下角的矩形面积 ，黄色面积是指(1,1)左上角到(x2,y1-1)右下角的矩形面积

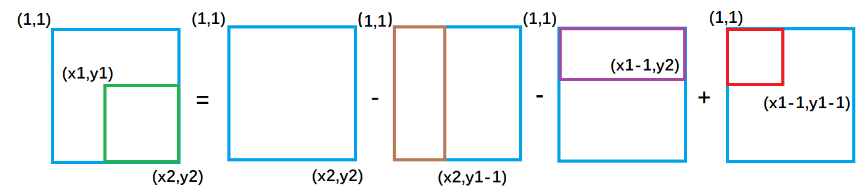
绿色矩形的面积 = 整个外围面积s[x2, y2] - 黄色面积s[x2, y1 - 1] - 紫色面积s[x1 - 1, y2] + 重复减去的红色面积 s[x1 - 1, y1 - 1]
所以公式

S[x1 ~ x2][y1 ~ y2] = s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]

来个模板题练练手 二维前缀和

差分

类似于数学中的求导和积分，差分可以看成前缀和的逆运算。

一维差分

模板

作用是可以快速的让序列多个区间加上相同的数，最后求序列

void insert(int l, int r, int c)
{
    s[l] += c;
    s[r + 1] -= c;
}
void solve(){
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    for (int i = 1; i <= n; i++)
        insert(i, i, a[i]);
    while (q--)
    {
        int l, r, c;
        scanf("%d%d%d", &l, &r, &c);
        insert(l, r, c);
    }
    for (int i = 1; i <= n; i++)
        s[i] += s[i - 1];
}

原理

s[i] = a[1] + a[2] + a[3] +...+ a[i]
所以s数组是a的前缀和的数组，a数组就是差分数组了
让s数组的l~r都加上c ，a[l]+=c,a[r+1]-=c;
所以s[l]~s[r] 都因为a[l]变成a[l]+c而都加了c，多加的在a[r+1]的地方减去就好了

来个模板题练练手 一维差分

二维差分

如果扩展到二维，我们需要让二维数组被选中的子矩阵中的每个元素的值加上c,是否也可以达到O(1)的时间复杂度。答案是可以的，考虑二维差分

模板

作用是让一块区间加上相同的数

void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1]+=c;   b[x1][y2+1]-=c; b[x2+1][y1]-=c; b[x2+1][y2+1]+=c;
}
int main ()
{
    for (int i=1;i<=n;i++)  for (int j=1;j<=m;j++)  insert(i,j,i,j,a[i][j]);
    while (q--)
    {
        int x1,x2,y1,y2,c;  cin>>x1>>y1>>x2>>y2>>c;
        insert(x1,y1,x2,y2,c);
    }
    for (int i=1;i<=n;i++)  for (int j=1;j<=m;j++)  
	b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];

原理

让a数组的x1 ~ x2,y1 ~ y2的所有区间都加上c

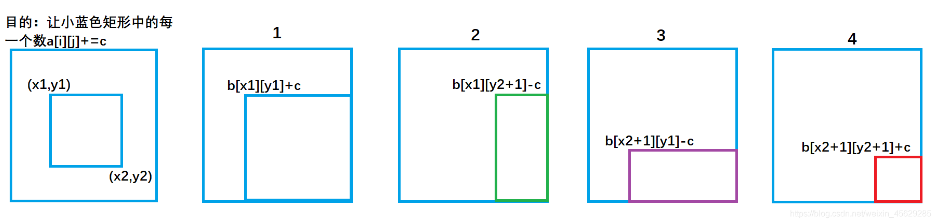
b[x1][ y1 ] +=c ; 对应图1 ,让整个a数组中蓝色矩形面积的元素都加上了c。
b[x1,][y2+1]-=c ; 对应图2 ,让整个a数组中绿色矩形面积的元素再减去c，使其内元素不发生改变。
b[x2+1][y1]- =c ; 对应图3 ,让整个a数组中紫色矩形面积的元素再减去c，使其内元素不发生改变。
b[x2+1][y2+1]+=c; 对应图4,,让整个a数组中红色矩形面积的元素再加上c，红色内的相当于被减了两次，再加上一次c，才能使其恢复。

来个模板题练练手 二维差分

题单

都是一些模板题，给大家熟悉一下
题单