python算法与数据结构-希尔排序算法(35)

一、希尔排序的介绍

　　希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。 希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的记录越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。　　

二、希尔排序的原理

　　在前面文章中介绍的直接插入排序，它对于已经基本有序的数据进行排序，效率会很高，而如果对于最初的数据是倒序排列的，则每次比较都需要移动数据，导致算法效率降低。

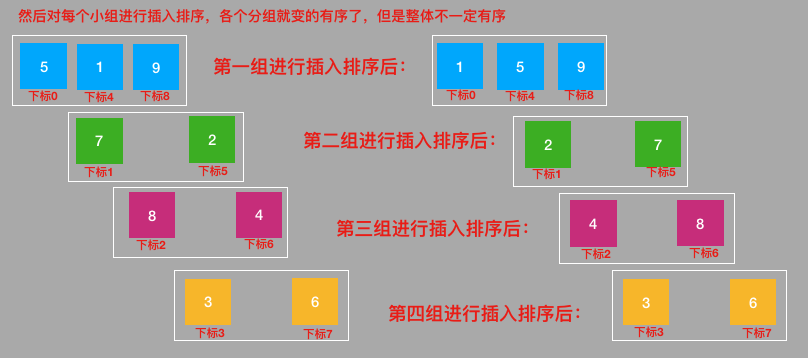
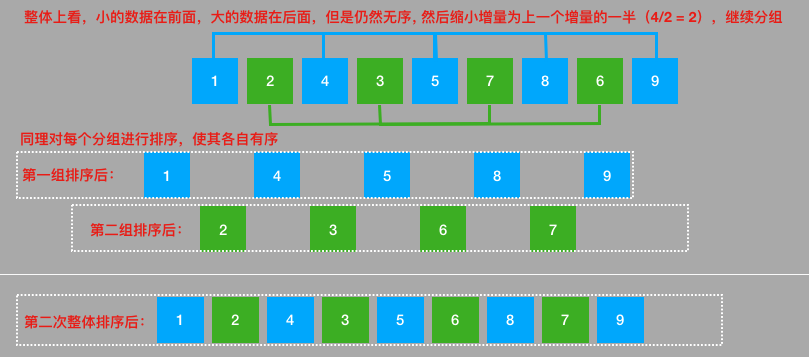
      希尔排序的基本思想就是：将需要排序的序列逻辑上划分为若干个较小的序列（但并非真的分割成若干分区），对这些逻辑上序列进行直接插入排序，通过这样的操作可使需要排序的数列基本有序，最后再使用一次直接插入排序。

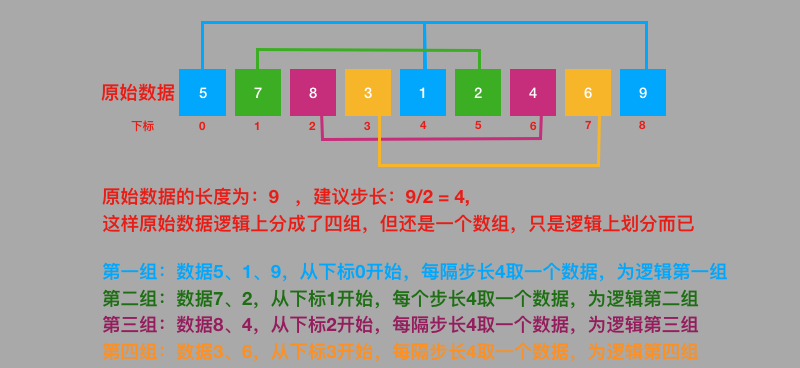
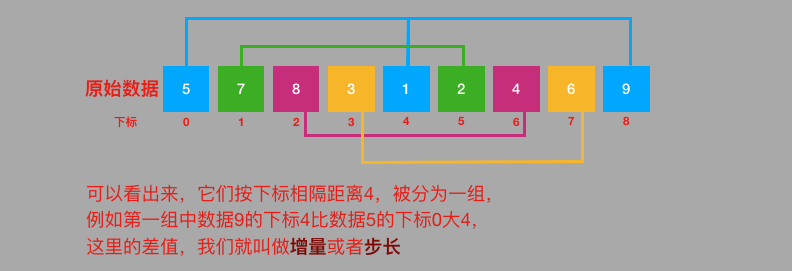
      在希尔排序中首先要解决的是怎样划分序列，对于子序列的构成不是简单地分段，而是采取将相隔某个增量的数据组成一个序列。一般选择增量的规则是：取上一个增量的一半作为此次子序列划分的增量，一般初始值元素的总数量的一半。

三、希尔排序的图解　

 

四、希尔排序的python代码实现

# 创建一个希尔排序的函数
def shell_sort(alist):
    # 需要排序数组的个数
    N = len(alist)
    # 最初选取的步长
    gap = N//2
    
    # 根据每次不同的步长，对分组内的数据进行排序
    # 如果步长没有减为1就继续执行
    while gap>0:
        # 对每个分组进行插入排序，
        # 因为插入排序从第二个元素开始，而这里第二个元素的下标就是gap
        # 所以i的起始点是gap
        for i in range(gap,N):
            # 控制每个分组内相邻的两个元素,逻辑上相邻的两个元素间距为gap，
            # j的前一个元素比它少一个gap距离，所以for循环中j的步长为 -gap
            for j in  range(i,0,-gap):
                # 判断和逻辑上的分组相邻的两个数据大小
                if alist[j]<alist[j-gap] and j-gap>=0:
                    # 交换
                    temp = alist[j]
                    alist[j] = alist[j-gap]
                    alist[j-gap] = temp
        # 改变步长
        gap = gap//2
    
    
numlist = [5,7,8,3,1,2,4,6,9]
print("排序前：%s"%numlist)
shell_sort(numlist)
print("排序后：%s"%numlist)

运行结果为：

排序前：[5, 7, 8, 3, 1, 2, 4, 6, 9]
排序后：[1, 2, 3, 4, 5, 6, 7, 8, 9]

五、希尔排序的C语言实现

#include <stdio.h>
// 创建一个希尔排序的函数
void shell_sort(int arr[],int arrLength,int gap)
{
    // 根据每次不同的步长，对分组内的数据进行排序
    // 如果步长没有减为1就继续执行
    while (gap>0)
    {
        // 对每个分组进行插入排序，
        // 因为插入排序从第二个元素开始，而这里第二个元素的下标就是gap，
        // 所以i的起始点是gap
        for (int i = gap; i<arrLength; i++)
        {
            // 控制每个分组内相邻的两个元素,逻辑上相邻的两个元素间距为gap，
            // j的前一个元素比它少一个gap距离，所以for循环中j每次减少一个gap
            // 因为j-gap是上一个元素的下标，也必须保证大于等于0
            for (int j = i; j>0&&j-gap>=0; j=j-gap)
            {
                // 判断和逻辑上的分组相邻的两个数据大小
                if (arr[j]<arr[j-gap])
                {
                    // 交换
                    int temp = arr[j];
                    arr[j] = arr[j-gap];
                    arr[j-gap] = temp;
                }
            }
        }
        gap = gap/2;
    }
}

int main(int argc, const char * argv[]) {
   
    // 定义数组
    int array[] = {5,7,8,3,1,2,4,6,9};
    // 希尔排序的声明
    void shell_sort(int arr[],int arrLength,int gap);
    // 计算数组长度
    int len = sizeof(array)/sizeof(int);
    // 制定gap为二分之一的长度
    int g = len/2;
    // 使用希尔排序
    shell_sort(array, len, g);
    // 验证
    for (int i = 0; i<len; i++)
    {
        printf("%d ",array[i]);
    }
    
    return 0;
}

运行结果为：

1 2 3 4 5 6 7 8 9

 

六、希尔排序的时间复杂度

• 最优时间复杂度：根据步长序列的不同而不同
• 最坏时间复杂度：O(n2)

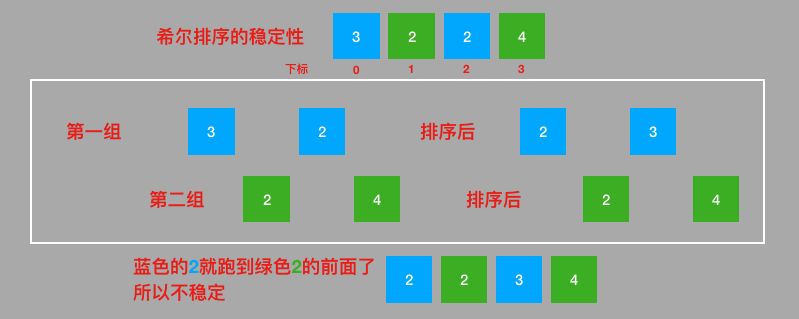
七、希尔排序的稳定性

　　由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的。