P9437 『XYGOI round1』一棵树 题解

首先这是一道很明显的换根 dp。

首先注意到要拼接数，所以我们可以先处理出 \(num_i=10^{x}\)，使得 \(10^x > a_i > 10^{x-1}\)，这样方便我们后面算贡献。

我们以这棵树为例子来推状态转移方程。

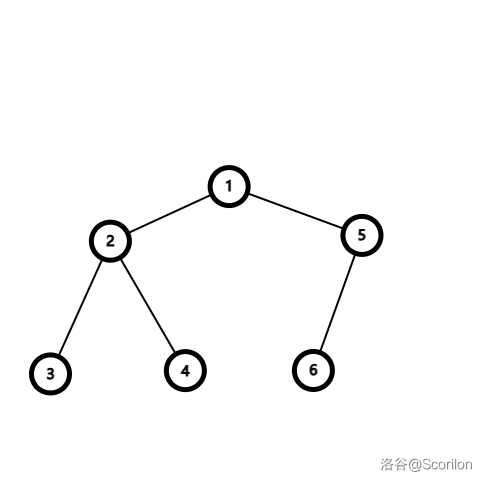
先假设 \(dp_u\) 表示以 \(1\) 为根时，从 \(u\) 的子树的点到 \(u\) 的权值和。

那么

\[dp_u=\sum_{v \in son_u} dp_v \times num_u+a_u \times siz_v \]

首先 \(dp_v \times num_u\) 是把前面已经拼好的数扩大 \(num_u\) 倍，然后 \(a_u \times siz_v\) 是 \(a_u\) 一共对包含它本身在内的子树节点数的贡献。

我们求出了以 \(1\) 为根时的贡献值后，设 \(f_u\) 表示以 \(u\) 为根时的值。

那么我们可以分为两部分考虑：

1. 属于 \(u\) 的子树的部分，那么这一部分很明显直接加上就可以，也就是 \(dp_u\)，例如上图我们已经求出了以 \(1\) 为根时的值，然后我们要从节点 \(1\) 转移到节点 \(2\)，那么属于节点 \(2\) 的子树部分的贡献就是 \(dp_2\)。

2. 不属于 \(u\) 的子树的部分，我们可以先利用 \(f_{fa}-sum\) 求出 \(fa\) 的子树中除去 \(u\) 的贡献的值，其中 \(sum\) 表示节点 \(u\) 对它的父节点即 \(fa\) 的贡献，根据我们上面的方程逆推回来可得 \(sum=dp_u \times num_{fa} + a_{fa} \times siz_u\)，然后再根据这个值来计算对 \(u\) 的贡献，那么还是带入上面的方程可得对 \(u\) 的贡献为 \((f_{fa}-sum) \times num_{u} + a_u \times (siz_1 - siz_{u})\).

因此状态转移方程为

\[f_u=dp_u+num_u \times (f_{fa}-(dp_u \times num_{fa}+a_{fa} \times siz_{u})) + a_u \times (siz_1-siz_u) \]

最后的答案就是

\[\sum_{i=1}^{n} f_i \]

#include <cstdio>

typedef long long ll;

const ll N=1e6+5;
const ll mod=998244353;

ll mo(ll x) {//取模，注意负数 
	return (x%mod+mod)%mod;
}

struct edge {
	ll v,nxt;
}G[N<<1];
ll h[N],idx;

void add(ll u,ll v) {
	G[++idx].v=v;
	G[idx].nxt=h[u];
	h[u]=idx;
}

ll n,a[N];
ll siz[N],num[N];
ll dp[N],f[N];

void dfs1(ll x,ll fa) {
	siz[x]=1,dp[x]=a[x];
	for(ll i=h[x];i;i=G[i].nxt) {
		ll v=G[i].v;
		if(v==fa) continue;
		dfs1(v,x);
		siz[x]+=siz[v];
		dp[x]=mo(dp[x]+mo(mo(dp[v]*num[x])+mo(siz[v]*a[x])));
	}
}

void dfs2(ll x,ll fa) {
	if(x!=1) {
		ll t1=mo(f[fa]-mo(mo(dp[x]*num[fa])+mo(a[fa]*siz[x])));
		f[x]=mo(mo(mo((siz[1]-siz[x])*a[x])+mo(t1*num[x]))+dp[x]);
	}
	for(ll i=h[x];i;i=G[i].nxt) {
		ll v=G[i].v;
		if(v==fa) continue;
		dfs2(v,x);
	}
}

int main() {
	scanf("%lld",&n);
	for(ll i=1;i<=n;i++) {
		scanf("%lld",&a[i]);
		num[i]=10;
		while(num[i]<=a[i]) num[i]*=10;
	}
	for(ll i=2;i<=n;i++) {
		ll x;
		scanf("%lld",&x);
		add(x,i);add(i,x);
	}
	dfs1(1,0);
	f[1]=dp[1];
	dfs2(1,0);
	ll ans=0;
	for(ll i=1;i<=n;i++) ans=mo(ans+f[i]);
	printf("%lld\n",ans);
	return 0;
}