Dynamic Dot Problem(EASY) 题解

模型建立

首先，题意应该很清楚了，我们可以拟一条数轴，通过样例一来辅助理解题目，建立模型。

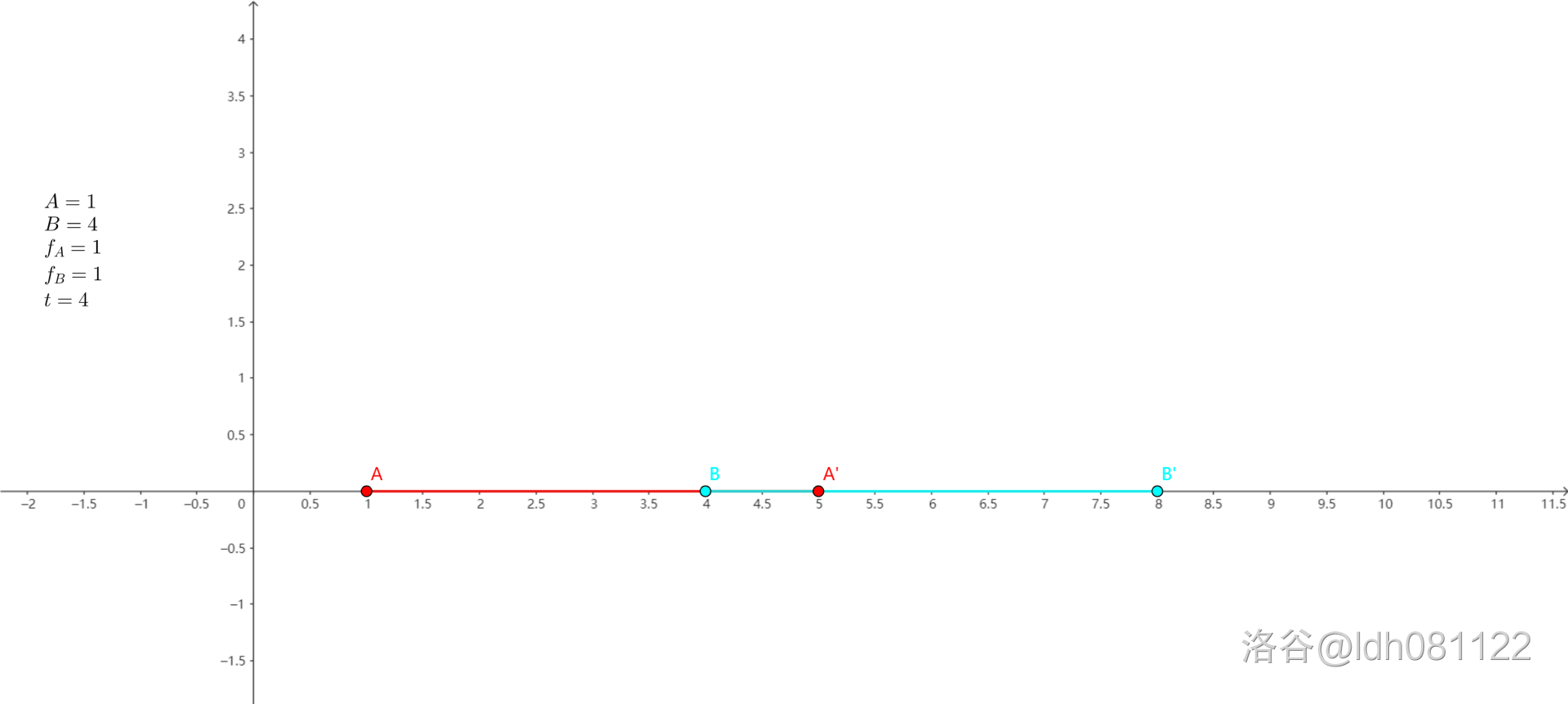
由此易得

\(A'=A+f_At\)

\(B'=B+f_Bt\).

因此我们就可以得出 \(A\ B\) 的位置，也易得 \(AB\) 的长度。

这是模型的建立，涉及到一点点入门的平面几何。

10pts/20pts/50pts/80pts做法

忽略了 \(A\ B\) 的大小关系，可以加绝对值即 abs() 或 if() 进行判断。

60pts做法

60pts 的做法是建立在模型、细节点都没有出错的情况下，没有开long long 造成的。

我们可以通过简单的计算来核定数据范围：

\(10^9+10^9 \times 10^9=10^{18}+10^9\)

\(-10^9-10^9 \times 10^9=-10^{18}-10^9\)

\(10^{18}+10^9+10^{18}+10^9=2 \times (10^{18}+10^9)\)

所以 int 存不下，要开 long long.

同时对于一些开了 long long 却还是 60pts 的同学，问题出在了计算过程中可能会爆 int.

100pts做法

避免了以上所有情况，就是满分做法了。

//B
#include <cstdio>
#include <iostream>

using namespace std;

int a,b;
int f1,f2;
int v1,v2;
int t;
long long new_a,new_b;

int main() {
    scanf("%d%d%d",&a,&f1,&v1);
    scanf("%d%d%d",&b,&f2,&v2);
    scanf("%d",&t);
    if(f1==1) new_a=1ll*a+(long long)v1*t;
    else new_a=1ll*a-(long long)v1*t;
    if(f2==1) new_b=1ll*b+(long long)v2*t;
    else new_b=1ll*b-(long long)v2*t;
    if(new_a<new_b) {
        long long x=new_a;
        new_a=new_b;
        new_b=x;
    }
    printf("%lld\n",new_a-new_b);
    return 0;
}

对于abs()

如果是用 cmath 库的函数，就会变成 \(5pts\)。原因是只有 float long double double 类型。

解决方法：

//1
#include <cstdlib>

abs();

//2
long long abs(long long x) {
	return x<0?-x:x;
}