Theory of Computation Review
Theorem. \(\mathsf{SPACE}(f(n)) \subseteq \mathsf{TIME}\left(2^{\mathcal O(f(n))}\right)\) when \(f(n) = \Omega(\log n)\).
Proof. A TM that decides a language always halts. Since it scans \(\le f(n)\) tapes, it can have at most \(2^{\mathcal O(f(n))}\) configurations. The total time to list all configurations is \(f(n) \cdot 2^{\mathcal O(f(n))} = 2^{\mathcal O(f(n))}\).
Theorem. \(\mathsf{NTIME}(f(n)) \subseteq \mathsf{SPACE}(f(n))\).
Proof. We can enumerate all guesses.
Theorem. \(\mathsf{NSPACE}(f(n)) \subseteq \mathsf{TIME}\left(2^{\mathcal O(f(n))}\right)\).
Proof. Construct a graph of the configurations, then check whether the accepting configuration is reachable from the initial configuration.
Theorem. PATH is in \(\mathsf{NL}\).
Proof. Non-deterministically walk through the graph, checking whether the current vertex is the target vertex.
Theorem. If \(A_1 \le_{\mathsf L} A_2\) and \(A_2 \in \mathsf L\), then \(A_1 \in \mathsf L\).
Proof. Suppose we want to check if \(w \in A_1\). We can simulate the log-space machine \(M\) on input \(f(w)\). We do not calculate \(f(w)\) directly (since \(f(w)\) may not be of log length), but each time \(M\) scans on a cell of the input tape we calculate that bit of \(f(w)\).
Theorem. PATH is \(\mathsf{NL}\)-complete.
Proof. The number of configurations is polynomial of \(n\). We can calculate the configuration graph in log space.
Theorem. \(\mathsf{NL} \subseteq \mathsf{P}\).
Proof. Obvious since PATH is in \(\mathsf P\).
Theorem. \(\mathsf{NSPACE}(\log n) \subseteq \mathsf{SPACE}(\log^2n)\).
Proof. Let \(f(u, v, d)\) denote if there is a path from \(u\) to \(v\) of length \(\le d\). Recursively calculate \(f(u, v, d)\) by $$f(u, v, d) = \bigvee_{w=1}^n \left(f(u, w, d/2) + f(w, v, d/2)\right).$$ To calculate \(f(s, t, |V|)\), the depth of the recursion is \(\log n\), thus the total space used is \(\mathcal O(\log^2 n)\).
Theorem. If \(\mathsf P = \mathsf{NP}\), then \(\mathsf{EXP} = \mathsf{NEXP}\).
Proof (padding argument). Need to show \(\mathsf{NEXP} \subseteq \mathsf{EXP}\). Suppose \(L \in \mathsf{NEXP}\) and NTM \(M\) decides \(L\) in time \(2^{n^k}\). Consider the language $$L' = \left{x1{2{|x|^k}} \mid x \in L \right},$$ where \(1\) is a symbol not in \(L\). Clearly a NTM decides this language in polynomial time. by \(\mathsf P = \mathsf{NP}\), there exists a DTM that decides \(L'\) in polynomial time. Hence, there exists another DTM that decides \(L\) in exponential time, so \(L \in \mathsf{NEXP}\).
Theorem (Savitch’s Theorem). For any \(S(n) \ge \log n\), \(\mathsf{NSPACE}(S(n)) \subseteq \mathsf{SPACE}(S^2(n))\).
Proof. Use similar padding argument as above. For \(L \in \mathsf{NSPACE}(S(n))\), we can construct \(L' \in \mathsf{NL}\), then \(L' \in \mathsf{SPACE}(\log^2 n)\), hence \(L \in \mathsf{SPACE}(S^2(n))\).
Corollary. \(\mathsf{PSPACE} = \mathsf{NPSPACE}\).
Theorem. NON-PATH is in \(\mathsf{NL}\).
Proof. Let \(R(i)\) denote the number of vectices reachable from \(s\) in \(i\) steps. We can compute \(R(i+1)\) from \(R(i)\) in log space by the following procedure:
cnt = 0
for u in V:
guess if u is reachable from s in i + 1 steps
if yes:
guess a path from s to u in i + 1 steps
if the path is invalid:
reject
cnt += 1
else:
k = 0
for v in V:
guess if v is reachable from s in i steps
if yes:
guess a path from s to v in i steps
if the path is invalid:
reject
if v == u or (v, u) is in E:
reject
k += 1
if k != R(i):
reject
R(i + 1) = cnt
Thus we can compute \(R(n)\). Then we delete \(t\) and compute \(R'(n)\). \(t\) is reachable from \(s\) iff \(R(n) = R'(n)\). The total space used is \(\mathcal O(\log n)\).
Corollary. \(\mathsf{NL} = \mathsf{coNL}\).
Proof. Since PATH is \(\mathsf{NL}\)-Complete, NON-PATH is \(\mathsf{coNL}\)-complete. Thus \(\mathsf{coNL} \subseteq \mathsf{NL}\). For any \(L \in \mathsf{NL}\), \(\bar L \in \mathsf{coNL}\), so \(\bar L \in \mathsf{NL}\), so \(L \in \mathsf{coNL}\). Hence, \(\mathsf{NL} = \mathsf{coNL}\).
Corollary. For any \(S(n) \ge \log(n)\), \(\mathsf{NSPACE}(S(n)) = \mathsf{coNSPACE}(S(n))\).
Proof. By a similar padding argument.
Theorem. \(\mathsf{NP} \subseteq \mathsf{PSPACE}\).
Proof. Obviously SAT is in \(\mathsf{PSPACE}\).
Theorem. TQBF is \(\mathsf{PSPACE}\)-Complete.
Proof. Only need to show that TQBF is \(\mathsf{PSPACE}\)-hard. For a polynomial space TM \(M\), let \(\psi(u, v, t)\) denote if configuration \(v\) is reachable from \(u\) in \(t\) steps. Then $$\psi(u, v, t) = (\exists m) (\psi(u, m, t/2) \wedge \psi(m, v, t/2)),$$ which is equivalent to $$(\exists m) (\forall a) (\forall b) (((a=u\wedge b=m) \vee (a=m\wedge b=v)) \to \psi(a, b, t/2)).$$ Since \(M\) runs in exponential time, the depth of the recursion is polynomial, thus the total space used is polynomial. Hence, TQBF is \(\mathsf{PSPACE}\)-hard and thus \(\mathsf{PSPACE}\)-complete.
Theorem. \(\mathsf{TIME}(\mathcal O(n^{1.1})) \ne \mathsf{TIME}(\mathcal O(n))\).
Proof. Consider the TM \(D\) that runs on the discription \(\langle M \rangle\) of a TM \(M\). \(D\) simulates \(M\) with input \(\langle M \rangle\) for \(|\langle M \rangle|^{1.1}\) steps. If accepts then reject, and otherwise accept.
Clearly \(D\) is in \(\mathsf{TIME}(\mathcal O(n^{1.1}))\). Suppose \(D \in \mathsf{TIME}(\mathcal O(n))\), and \(M'\) decides \(L(D)\) in \(cn\) time, then consider \(D(\langle M' \rangle) = M'(\langle M' \rangle)\). We can make \(\langle M' \rangle\) not too small so that $$|\langle M' \rangle|^{1.1} > c |\langle M' \rangle| \log \left(|\langle M' \rangle|\right),$$ then the simulation can finish, hence contradiction.
Theorem (Time Hierarchy Theorem). For any time constructible function \(f:\mathbb N \to \mathbb N\), there exists a language \(L\) that is decidable in time \(f(n)\) but not in time \(o(f(n)/\log f(n))\).
Theorem (Space Hierarchy Theorem). For any space constructible function \(f:\mathbb N \to \mathbb N\), there exists a language \(L\) that is decidable in space \(f(n)\) but not in space \(o(f(n))\).
Corollary. \(\mathsf L \ne \mathsf{PSPACE}\).
Theorem. There exists an oracle \(B\) for which \(\mathsf{P}^B \ne \mathsf{NP}^B\).
Proof. For a language \(B\) we define \(L(B) = \{1^k \mid \exists x \in B, |x| = k\}\). Consider finding a language \(B\) such that \(L(B) \in \mathsf{NP}^B - \mathsf P^B\). Obviously \(L(B) \in \mathsf{NP}^B\). Now we construct a \(B\) satisfying \(L(B) \not\in \mathsf P^B\).
We enumerate all deterministic OTMs \(M_0, M_1, \cdots\) and maintain two sets \(B, X\). For each \(i\), let \(n\) be some integer that \(n > |x|\) for all \(x \in B \cup X\). We simulate \(M_i(1^n)\) for \(n^{\log n}\) steps. When \(M_i\) makes a query \(q\) to the oracle, if \(|q| < n\) then answer with \(B\), and otherwise answer no and add \(q\) to \(X\). If \(M_i\) accepts, then add all strings in \(\{0, 1\}^n\) to \(X\). If \(M_i\) rejects, find some \(x \in \{0, 1\}^n\) such that \(x \not\in X\) and add \(x\) to \(B\).
If \(M_i\) accepts \(1^n\) then \(L(B) \ne L(M_i)\). If \(M_i\) rejects \(1^n\), then since \(n^{\log n} < 2^n\) we can find such \(x\), so \(L(B) \ne L(M_i)\). If \(M_i\) is in \(\mathsf{TIME}(\mathcal O(n^c))\), then we can choose sufficiently large \(n\) such that \(n^{\log n} > n^c\). Therefore for any \(M_i\), \(L(B) \ne L(M_i)\), hence \(L(B) \not\in \mathsf P^B\).
Theorem. For undirected unweighted graph \(G\) we can find a \(2\)-additive spanner of \(G\) with \(\mathcal O(n^{3/2})\) edges.
Proof. Randomly sample \(n^{1/2}\) vectices and denote the set as \(W\). The spanner \(S\) first contains the shortest path trees from each vertex in \(W\). For all \(u \not\in W\), if \(u\) has a neighbor \(v \in W\), then add the edge \((u, v)\) to \(S\). Otherwise, add all edges adjacent to \(u\) to \(S\). We note that if \(\deg u = \Omega(n^{1/2})\) then w.h.p. it is adjacent to a vertex in \(W\).
Now consider the shortest path from \(u\) to \(v\). If \(u\) or \(v\) is in \(W\) then obviously correct. Otherwise, if the first edge \((u, u') \in S\) we can recursively consider \((u', v)\), and otherwise we can find \((u, u') \in E\) s.t. \(u' \in W\), then we can find a path from \(u\) to \(v\) in \(S\) of length \(\le d(u, v) + 2\).
Theorem. Miller-Rabin primality test is correct with probability \(\ge 1 - 2^{-t}\), where \(t\) is the number of iterations.
Proof. We can prove that for every odd composite \(n\) we can find \(x\) such that \((x, n) = 1\) and \(x^{(n-1)/2^k} \not\equiv \pm 1 \pmod n\) for some \(k\). Then we can prove that at least onf half of elements in \(\mathbb Z_n^*\) are such \(x\).
Theorem. Suppose \(x\) is a binary random variable with \(\Pr[x=1] = 1/2 + \epsilon\) and \(\Pr[x=0] = 1/2 - \epsilon\). For some integer \(k\) let \(m = k/\epsilon^2\). If we sample \(x\) for \(m\) times, then the probability that the majority of the samples are \(1\) is \(1 - \exp(-\Omega(k))\).
Proof. $$\sum_{i=0}^{\frac m 2} \binom m i \left(\frac12 + \epsilon\right)^i \left(\frac12 - \epsilon\right)^{m-i} \le 2^m \left(\frac12 + \epsilon\right)^{\frac m 2} \left(\frac12 - \epsilon\right)^{\frac m 2} = \left(1 - 4\epsilon^2 \right)^{\frac{k}{2 \epsilon^2 }} \le \text e^{-2k}.$$
Theorem (Schwartz-Zippel). Let \(p(x_1, x_2, \cdots, x_n)\) be a total degree \(d\) non-zero polynomial and let \(S\) be any subset of integers. Then $$\Pr_{r_1, r_2, \cdots, r_n \in S}[p(r_1, r_2, \cdots, r_n) = 0] \le \frac{d}{|S|}.$$
Proof. Induct on \(n\). If \(n=1\) by the fundemental theorem of algebra the statement is true. When \(n > 1\) we write the polynomial as \(\sum_{i=0}^k x_1^i p_i(x_2, \cdots, x_n)\). In case that \(p_k(x_2, \cdots, x_n) \ne 0\) the whole polynomial is \(0\) w.p. \(\le k/|S|\) (the probability is taken by \(x_1\)). Hence, $$\Pr[p(r_1, \cdots, r_n) = 0] \le \frac{k}{|S|} + \Pr[p_k(r_2, \cdots, r_n) \ne 0] \le \frac{d}{|S|}.$$
Theorem. \(\mathsf{ZPP} = \mathsf{RP} \cap \mathsf{coRP}\).
Proof. \(\mathsf{RP} \cap \mathsf{coRP} \subseteq \mathsf{ZPP}\): For any \(L \in \mathsf{RP} \cap \mathsf{coRP}\), let \(M_1 \in \mathsf{RP}\) and \(M_2 \in \mathsf{coRP}\) both decide \(L\). For any input \(w\) we run \(M_1\) and \(M_2\). If \(M_1\) accepts then accept. If \(M_2\) rejects then reject. Otherwise, repeat. The expected time is polynomial.
\(\mathsf{ZPP} \subseteq \mathsf{RP} \cap \mathsf{coRP}\): For \(\mathsf{RP}\), simulate the \(\mathsf{ZPP}\) algorithm for double its expected running time. If the algorithm halts then return its result. Otherwise, reject. We notice that the algorithm halts under the simulation w.p. \(\ge 1/2\), so the correctness is guaranteed.
Theorem. \(\mathsf{RP} \subseteq \mathsf{NP}\).
Proof. Trivial.
Theorem. If \(\mathsf P = \mathsf{NP}\), then \(\mathsf{PH} = \mathsf P\).
Proof. We prove \(\Sigma_n = \mathsf P\) for all \(n \ge 0\) by induction. We see that $$\Sigma_n = \mathsf{NP}^{\Sigma_{n-1}} = \mathsf{NP}^{\mathsf P} = \mathsf P^{\mathsf P} = \mathsf P.$$
Corollary. If \(\Sigma_i = \Pi_i\), then \(\mathsf{PH} = \Sigma_i\).
Theorem. \(\mathsf{BPP} \subseteq \mathsf{PH}\).
Proof. Use a \(m\)-bit random string \(r\) to represent the randomness. By error reduction for any \(L \in \mathsf{BPP}\) we can find a TM \(M\) such that $$x \in L \Rightarrow \Pr_r[M(x ,r) = 1] \ge 1 - \frac{1}{2m}$$ and $$x \not\in L \Rightarrow \Pr_r[M(x, r) = 1] \le \frac{1}{2m}.$$ Now we claim that $$x \in L \Leftrightarrow (\exists r_1)(\exists r_2) \cdots (\exists r_m) (\forall s) (\exists i) (M(x, r_i \oplus s) = 1).$$
If \(x \in L\) then $$\Pr_{r_1, r_2, \cdots, r_m, s}[(\exists i)(M(x, r_i \oplus s)) = 1] \le 1 - \left(\frac{1}{2m}\right)^m,$$ so $$\Pr_{r_1, r_2, \cdots, r_m}[(\forall s)(\exists i)(M(x, r_i \oplus s)) = 1] \le 1 - 2^m \left(\frac{1}{2m}\right)^m > 0,$$ thus such \((r_1, r_2, \cdots, r_m)\) must exist.
If \(x \not\in L\) then for any \((r_1, r_2, \cdots, r_m)\), $$\Pr_s[(\exists i)(M(x, r_i \oplus s) = 1)] \le \sum_i \Pr_s[M(x, r_i \oplus s) = 1] \le m \cdot \frac{1}{2m} < 1,$$ so there must exists \(s\) such that \((\forall i)(M(x, r_i \oplus s) = 0)\).
Therefore, we see that \(\mathsf{BPP} \subseteq \Sigma_2\). Since \(\mathsf{BPP} = \mathsf{coBPP}\), \(\mathsf{BPP} \subseteq \Sigma_2 \cap \Pi_2\). Hence, \(\mathsf{BPP} \subseteq \mathsf{PH}\).
Theorem. GNI is in \(\mathsf{IP}\).
Proof. Suppose the prover wants to prove that \(G_0 \not\cong G_1\). The verifier can randomly choose a bit \(b\) and a permutation \(\pi\) and send \(\pi(G_b)\) to the prover. The prover need to tell if \(b\) is \(0\) or \(1\). The verifier can repeat this procedure to reduce the error probability.
Theorem. #SAT is in \(\mathsf{IP}\).
Proof.
Attempt: Suppose the prover claims that \(\phi(x_1, x_2, \cdots, x_n)\) has \(k\) satisfying assignments. The prover sends \(k_0, k_1\) to the verifier, claiming that \(\phi(0, x_2, \cdots, x_n)\) has \(k_0\) satisfying assignments and \(\phi(1, x_2, \cdots, x_n)\) has \(k_1\) satisfying assignments. The verifier randomly chooses a bit \(b\), set \(x_1 = b\), and send the bit to the prover. The prover need to recursively prove that \(\phi(b, x_2, \cdots, x_n)\) has \(k_b\) satisfying assignments. In the end the verifier can check itself.
The only problem is that if the prover tries to cheat, it can win w.p. \(1 - 2^n\), which is too high. The idea for solving this problem is to transfer \(\phi\) into a polynomial and extend the range from \(\{0, 1\}\) to some larger field.
The first part is not hard. We can change \(\phi\) to polynomial \(p_{\phi}\) by applying $$\neg a \to (1-a), \quad (a \vee b) \to 1 - (1-a)(1-b), \quad (a \wedge b) \to ab.$$
Let \(F\) be a field with \(q > 2^n\) elements. We want to find $$\sum_{x_1 \in {0, 1}} \sum_{x_2 \in {0, 1}} \cdots \sum_{x_n \in {0, 1}} \phi(x_1, x_2, \cdots, x_n).$$ This time the prover can ask the prover to give a polynomial \(k(z)\) such that $$k(z) = \sum_{x_2 \in {0, 1}} \cdots \sum_{x_n \in {0, 1}} \phi(z, x_2, \cdots, x_n).$$ The prover checks iff \(k(0) + k(1) = k\), sends random \(z \in F\). Similarly, they repeat the procedure recursively. The difference is that if \(k(z)\) is not real, the probability of choosing a \(z\) such that \(k(z)\) is not the same as its definition is \(\ge 1 - d/q \ge 1 - d/2^n\). The probability of choosing such \(z\) in all steps is \(\ge (1-d/2^n)^n \ge 1 - \text{poly}(n)/2^n > 2/3\).
Corollary. \(\mathsf{coNP} \subseteq \mathsf{IP}\).
Proof. That's because we can reduce TAUTOLOGY to #SAT, and the former is \(\mathsf{coNP}\)-Complete.
Theorem. \(\mathsf{IP} = \mathsf{PSPACE}\).
Proof. \(\mathsf{IP} \subseteq \mathsf{PSPACE}\): Enumerate all possible interactions and calculate acceptance probability.
\(\mathsf{PSPACE} \subseteq \mathsf{IP}\): Consider TQBF. We see that \((\forall x_1) (\exists x_2) \cdots (\exists x_n) \phi(x_1, x_2, \cdots, x_n)\) is true iff $$\prod_{x_1\in{0, 1}} \sum_{x_2\in{0, 1}} \cdots \sum_{x_n\in{0, 1}} \phi(x_1, x_2, \cdots, x_n) > 0.$$ However, we cannot directly use the previous proof, since the degree of this polynomial may be exponential in \(n\). We notice that we only care about \(x \in \{0, 1\}\), so for any polynomial \(p(x_1, x_2, \cdots, x_n)\) we can use $$x_i p(x_1, \cdots, x_{i-1}, 1, x_{i+1}, \cdots, x_n) + (1-x_i) p(x_1, \cdots, x_{i-1}, 0, x_{i+1}, \cdots, x_n)$$ to replace \(p\), so that we can reduce the degree of \(x_i\). We do the reduce for every variable after each \(\sum\) and \(\prod\), so the degree can be linear to \(|\phi|\). The rest part is similar to the previous proof.
Therefore, \(\mathsf{IP} = \mathsf{PSPACE}\).
Corollary. \(\mathsf{AM} \subseteq \mathsf{IP}\).
Proof. The proof of \(\mathsf{PSPACE} \subseteq \mathsf{IP}\) dose not need any private randomness.
Remark. This corollary shows that public coins are at least as powerful as private coins.
Theorem. Let \(D(f)\) and \(C(f)\) denote the decision tree complexity and the certificate complexity of a function \(f:\{0, 1\}^n \to \{0, 1\}\), respectively. We have \(D(f) \le C(f)^2\).
Proof. We notice that every \(0\)-certificate must intersect with every \(1\)-certificate. Let \(S\) be any \(0\)-certificate of \(f(\cdot)\). We enumerate all bits in \(S\), and recursively call the corresponding decision trees (\(2^{|S|}\) decision trees in total). Since after each recursive call the maximum size of \(1\)-certificate is reduced by at least \(1\), the recursive depth is \(\le C(f)\). Thus the total depth of the decision tree is \(\le C(f)^2\).
Theorem. For any langauge \(L\), \(L \in \mathsf P\) iff there exists a logspace uniform, polynomial size circuit family \(\{C_n\}\) that decides \(L\).
Proof. \(\mathsf P \subseteq \mathsf{P/poly}\): We notice that the \(i\)-th character of the configuration at time \(t\) can be decided by the \((i-1)\)-th, \(i\)-th, and \((i+1)\)-th characters of the configuration at time \(t-1\). Thus we can use a circuit family to generate the table of computation history. Not hard to show that the circuit family is logspace uniform and polynomial sized.
\(\mathsf{P/poly} \subseteq \mathsf P\): We can use a TM to simulate the circuit family.
Theorem (Karp-Lipton). If SAT has poly-size circuits, then \(\mathsf{PH}\) collapses to the second level.
Proof. Only need to show \(\Pi_2 \subseteq \Sigma_2\). We see that $${x: (\forall y) (\exists z) (x, y, z) \in R}$$ is equivalent to $${x: (\exists C) (\forall y) \left(C((\exists z) (x, y, z) \in R) = 1\right)}.$$ Since \((\exists z) (x, y, z) \in R\) is in \(\mathsf{NP}\), such \(C\) exists, and we can simulate it in polynomial time.
Hence, \(\Pi_2 \subseteq \Sigma_2\), so \(\mathsf{PH} = \Sigma_2 = \Pi_2\).
Theorem (Shannon). A random function \(f:\{0, 1\}^n \to \{0, 1\}\) requires a circuit of size \(\Omega(2^n/n)\) to compute w.p. \(1 - o(1)\).
Proof. # of circuits with \(n\) inputs and size \(s\) is at most $$C(n, s) = \left(3(s+n)2\right)s.$$ We have $$C(n, c2^n/n) < \left(c' \cdot \frac{2{2n}}{n2}\right)^\frac{c 2^n}{n} = \mathcal O\left(\frac{1}{n^2}\right) \cdot 2{2c2n} = \mathcal o(1) \cdot 2{2n}.$$ Since the number of functions is \(2^{2^n}\), we see that w.p. \(1 - o(1)\) a random function cannot be computed by circuits of size \(\le c2^n/n\).
Theorem. \(\mathsf{EXPSPACE} \not\subseteq \mathsf{P/poly}\).
Proof. Let \(f_n\) denote the first function which needs circuit of size \(\Omega(2^n/n)\). Let \(L = \{x:f_{|x|}(x) = 1\}\). We see that \(L\) is not in \(\mathsf{P/poly}\). Since we can enumerate all functions and circuits of \(\mathcal O(2^n/n)\) size, \(L \in \mathsf{EXPSPACE}\).
Corollary. \(\mathsf{EXP}^{\Sigma_2} \not\subseteq \mathsf{P/poly}\).
Proof. Instead of enumerating all functions we do a binary search. We just need to ask the oracle to solve $$(\exists f \in [f_1, f_2])(\forall C, |C| = \mathcal O(2^n/n)) (C \ne f).$$
Question: To check whether \(C = f\) we need to verify \(2^n\) bits. Is it really in \(\Sigma_2\)?
Answer: Yes, since the input length is also \(\mathcal O(2^n)\).
Corollary. \(\mathsf{NEXP}^{\mathsf{NP}} \not\subseteq \mathsf{P/poly}\).
Proof. If \(\mathsf{NEXP}^{\mathsf{NP}} \subseteq \mathsf{P/poly}\) then \(\mathsf{NP} \subseteq \mathsf{P/poly}\), so \(\mathsf{PH}\) collapses to the second level. Hence, $$\mathsf P^{\Sigma_2} = \Sigma_2 = \mathsf{NP}^{\mathsf{NP}}.$$ By padding argument, \(\mathsf {EXP}^{\Sigma_2} \subseteq \mathsf{NEXP}^{\mathsf{NP}}\), but we have shown that \(\mathsf{EXP}^{\Sigma_2} \not\subseteq \mathsf{P/poly}\).
Theorem. \(L \in \mathsf{NC}^1\) iff decidable by polynomial-size uniform family of Boolean formulas.
Proof. Too lazy to write.
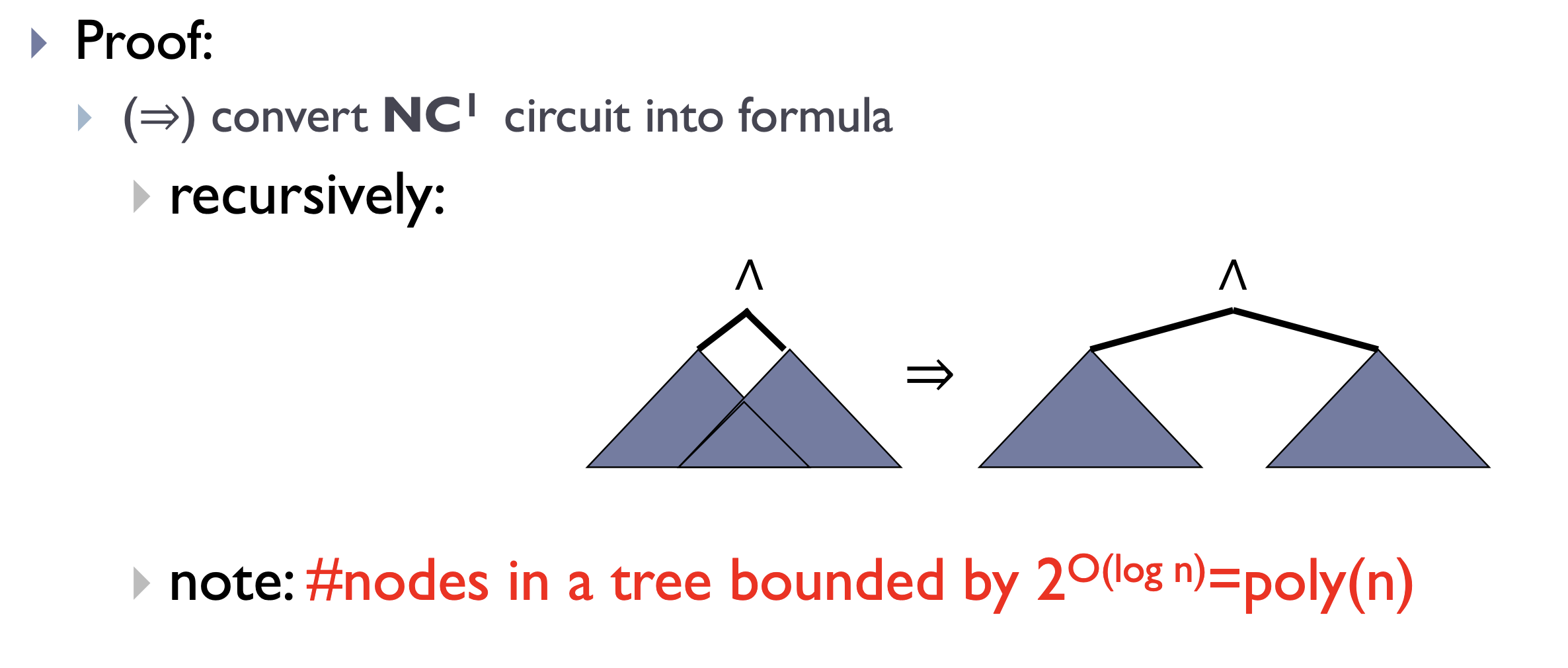
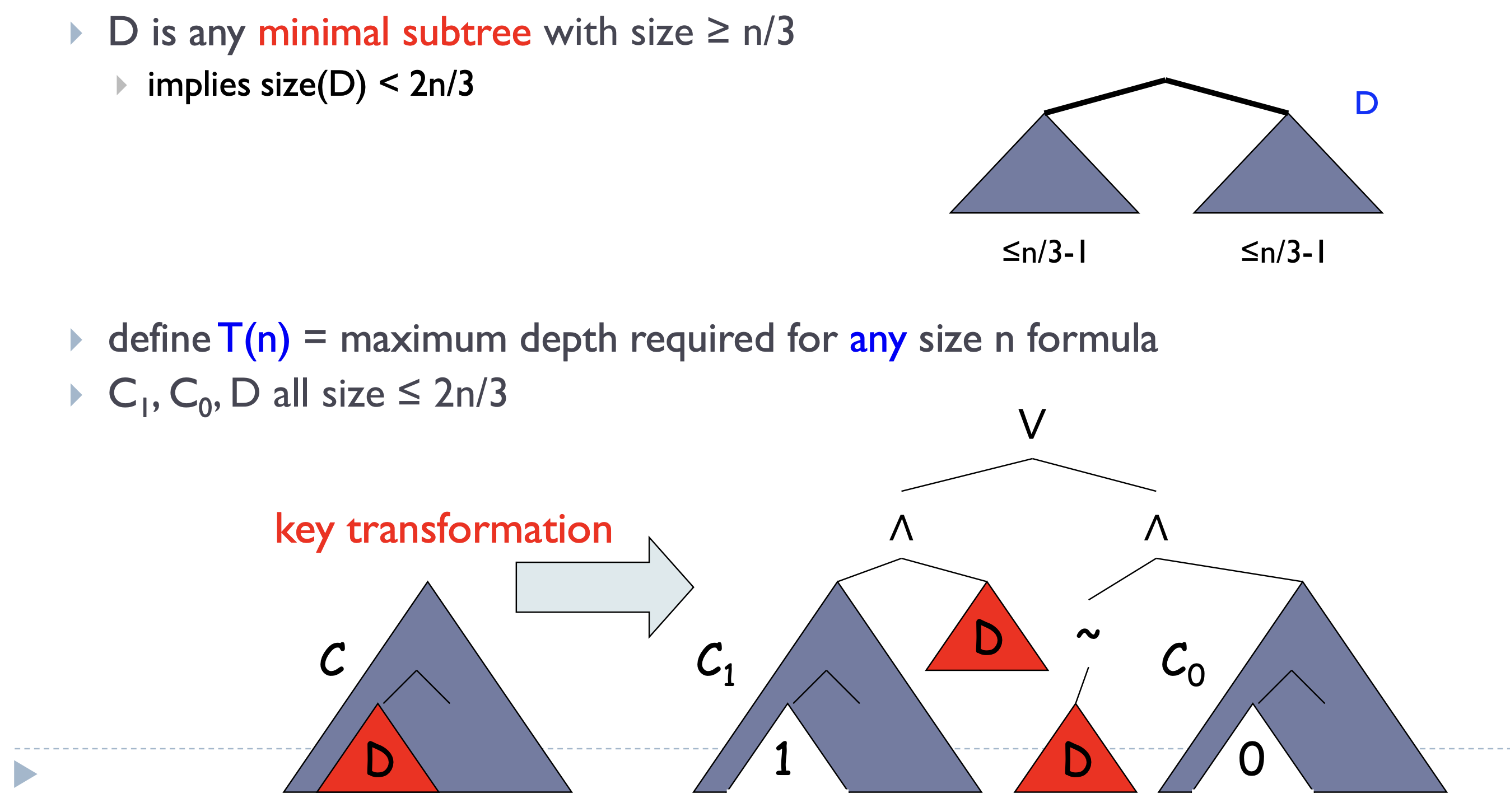
Theorem. \(\mathsf{NC} \subseteq \mathsf P\) and \(\mathsf{NC}^1 \subseteq \mathsf L\).
Proof. Trivial.
Theorem. \(\mathsf{NL} \subseteq \mathsf{NC}^2\).
Proof. We can use a log-depth circuit to calculate the boolean matrix multiplication. Therefore, we can calculate \(A^n\) in \(\mathcal O(\log^2 n)\) depth, where \(A\) is the adjacency matrix.
Theorem. Binary number addition is in \(\mathsf{AC}^0\).
Proof. Trivial.
Theorem. Parity is not in \(\mathsf{AC}^0\).
Proof. We use two lemmas to prove the statement.
Lemma 1. Let \(C\) be a circuit of size \(s\) and depth \(d\), then \(C\) is \(99\%\) approximated by a polynomial of degree \((\log s)^{\mathcal O(d)}\) over \(\mathbb Z_3 = \{-1, 0, 1\}\).
Proof. Let \(x_1 \vee x_2 \cdots \vee x_n \to \sum a_i x_i\), where \(a_i\) are randomly sampled from \(\mathbb Z_3\). We use De Morgan's law to eliminate \(\wedge\). By sampling \(\mathcal O(\log s)\) times we can reduce the error probability to \(< 1/(100s)\).
Lemma 2. Parity cannot be \(99\%\) approximated by a polynomial of degree \(c \cdot n^{1/2}\) over \(\mathbb Z_3\).
Proof. We can transfer any polynomial from \(\{0, 1\}^n \to \{0, 1\}\) to \(\{-1, 1\}^n \to \{0, 1\}\) with the same degree by \(0 \to -1\) and \(1 \to 1\). In \(\mathbb Z_3\) the transform is \(f(x_1, \cdots, x_n) \to -f(-x_1-1, \cdots, -x_n-1)-1\).
The parity function is transformed to \(\prod x_i\). Suppose \(q\) is a polynomial of degree \(c \cdot n^{1/2}\) that approximates the parity functio over \(S \subseteq \{-1, 1\}^n\), where \(|S| > 0.99 \cdot 2^n\). We see that any function over \(\{-1, 1\}^n \to \{0, 1\}\) is equivalent to a polynomial of degree \(n\) in \(\mathbb Z_3\) because it is equivalent to a multi-linear polynomial. We also see that for any monomial of degree \(\ge n/2\) we can multiply it by \(q(x_1, x_2, \cdots, x_n) / x_1x_2\cdots x_n\) to make the degree \(\le n/2 + c \cdot n^{1/2}\), thus any function over \(S \to \{-1, 1\}\) is of degree \(n/2 + c \cdot n^{1/2}\).
The number of functions over \(S \to \{-1, 1\}^n\) is \(> 2^{0.99 \cdot 2^n}\), and the number of polynomials of degree \(\le n/2 + c \cdot n^{1/2}\) is $$3{\sum_{i=0}{n/2 + c \cdot n^{1/2}} \binom n i}.$$ We can choose \(c\) small so that the former is large than the latter.
Then we are done.
Theorem. Let \(p\) and \(q\) be distinct primes, then \(\text{MOD}_q \not\in \mathsf{AC}^0[p]\).
Proof. I don't know.
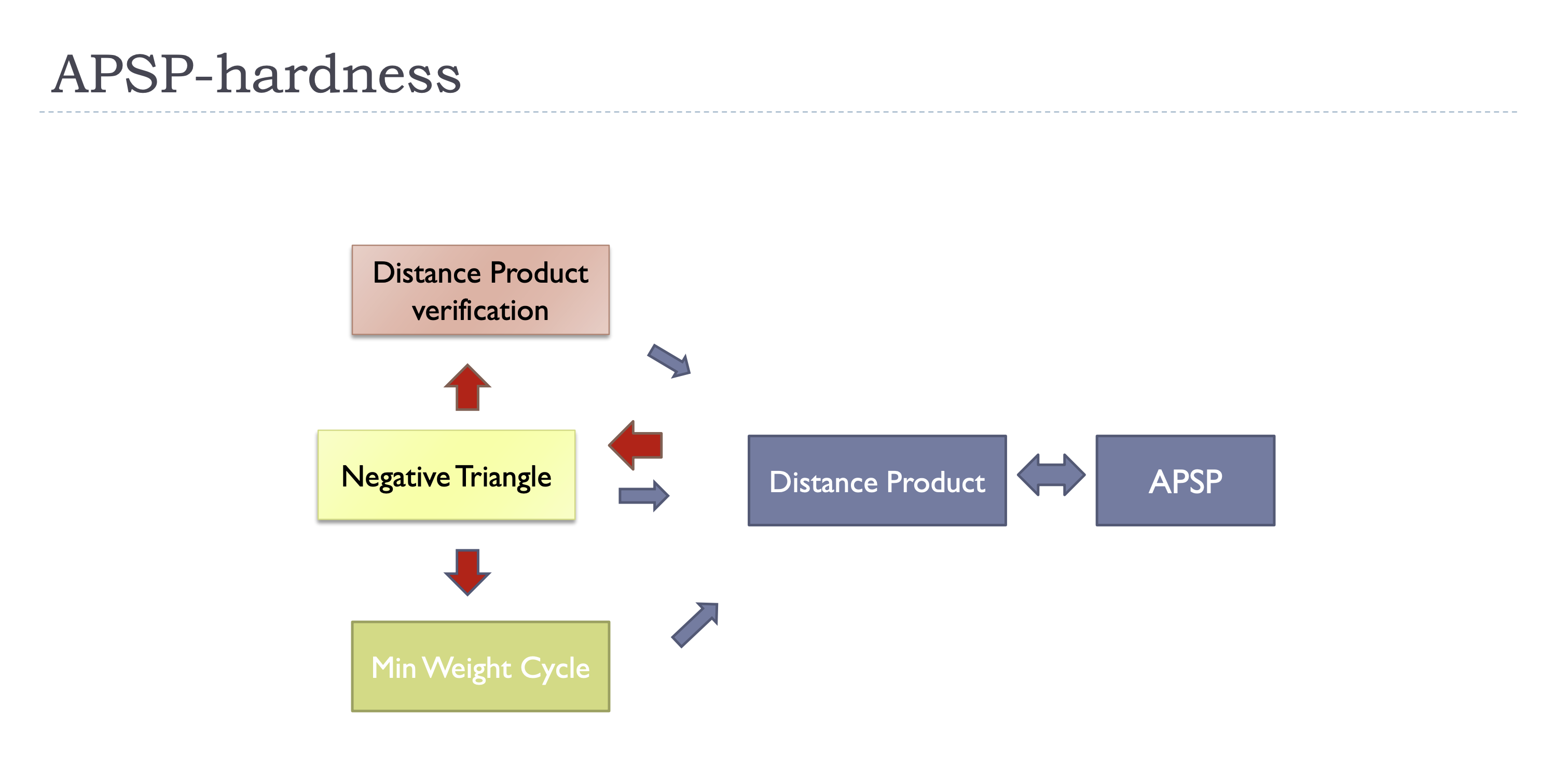
Distance Product \(\Rightarrow\) APSP: Tripatite graph. \(w(u_1, v_2) = A_{u, v}\), \(w(u_2, v_3) = B_{u, v}\).
APSP \(\Rightarrow\) Distance Product: Calculate \(A^n\), where \(A\) is the adjacency matrix.
Distance Product verification \(\Rightarrow\) Distance Product: Trivial.
Negative Triangle \(\Rightarrow\) Distance Product: For all \((u, v)\) check if \(A_{u, v} + A^2_{v, u} < 0\).
Min Weight Cycle \(\Rightarrow\) APSP: Trivial.
Distance Product \(\Rightarrow\) Negative Triangle: We introduce a middle problem: All-Pair Negative Triangle. Distance Product \(\Rightarrow\) All-Pair Negative Triangle: Tripatite graph. We guess the result \(C\). \(w(u_1, v_2) = -A_{u, v}\), \(w(u_2, v_3) = -B_{u, v}\), \(w(u_3, v_1) = C_{u, v}\). Run APNT on this graph to know if each \(C_{u, v}\) is \(\ge\) / \(<\) then result. All-Pair Negative Triangle: Separate each partition of the tripatite graph into \(s\) parts, each part of size \(n/s\). Enumerate \((n/s)^3\) triples, keep running the Negative Triangle algorithm to check if there is a negative triangle. If yes, delete one edge in the traignle and repeat. Suppose Negative Triangle can be solved in \(T(n)\) then APNT can be solved in \(\mathcal O(((n/s)^3 + n^2) T(s))\), so we only need to let \(s = n^{1/3}\).
Negative Triangle \(\Rightarrow\) Min Weight Cycle: Suppose edge weights are in \([-M, M]\). We add \(8M\) to all weights so that the length of any triangle is \(\le 27M\) and the length of any cycle with \(\ge 4\) edges is \(\ge 28M\).
Negative Triangle \(\Rightarrow\) Distance Product Verification: For all \((i, j)\) we just need to check if \(\min\{\min_k( A_{i, k} + A_{k, j}), -A^{\mathsf T}{(i, j)}\} = -A^{\mathsf T}{(i, j)}\). Not hard to use Distance Product to represent.
Theorem. \(3\)-SAT has an \(\mathcal O((4/3)^n)\) algorithm.
Proof. 
The winning propability is $$\ge \sum_{k=0}^n \binom n k 2^{-n} \left(\frac13\right)^k = \left(\frac23\right)^n.$$
Hence the expected number of repetitions is \(\mathcal O(1.5^n)\).
Now we change the \(\le n\) in the algorithm to \(\le 3n\). The probability of the difference from \(j\) to \(0\) in \(j+2i\) steps is $$\binom{j+2i}{i} \cdot \frac{j}{j+2i} \cdot \left(\frac13\right)^{j+i} \left(\frac23\right)^i \ge \frac13 \binom{j+2i}{i} \cdot \left(\frac13\right)^{j+i} \left(\frac23\right)^i.$$ When \(i=j\), the value is $$\frac13 \binom{3j}{j} \cdot \left(\frac13\right)^{2j} \left(\frac23\right)^j = \left(\frac12\right)^{j - o(j)}.$$ Sum over \(j\) gives $$2^{-n} \sum_{j=0}^n \binom n j \left(\frac12\right)^j = \left(\frac34\right)^n.$$
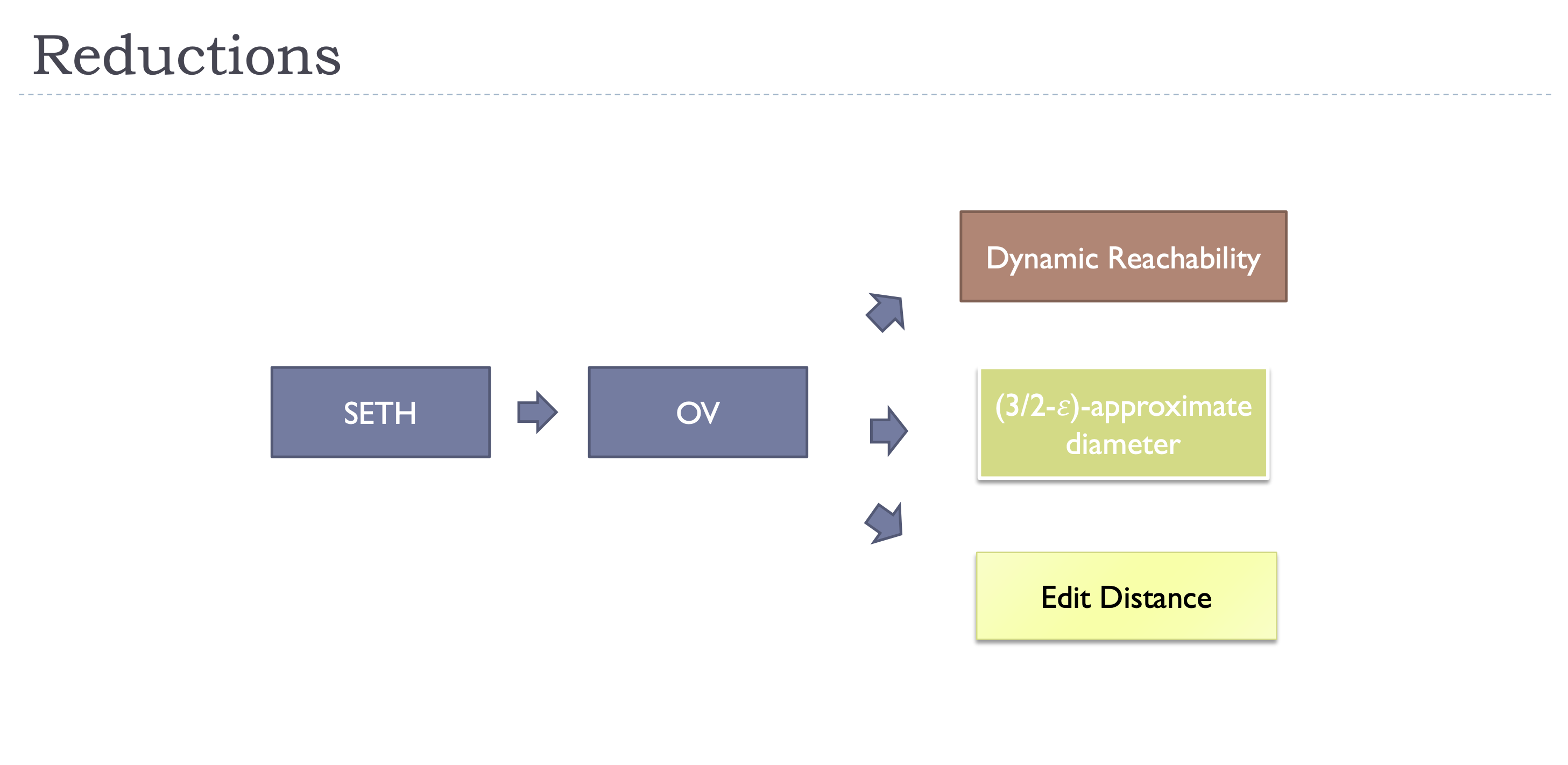
SETH \(\Rightarrow\) OV: Only consider the case of \(m = \mathcal O(n)\). Partition the variables into \(V_1, V_2\), on \(n/2\) variables each. For each assignment of \(V_1\) we construct a vector of length \(m+2\): \((0, 1, y_1, y_2, \cdots, y_m)\), where \(y_i\) is the value of the \(i\)-th clause only containing variables in \(V_1\) under the assignment. Similarly for each assignment of \(V_2\) we generate \((1, 0, y_1, y_2, \cdots, y_m)\). It's not hard to show that having a satisfying assignment is equivalent to having two vectors orthogonal to each other. Hence, if OV has an \(\mathcal O(n^{2-\epsilon})\) algorithm then \(k\)-SAT has an \(\mathcal{O}\left(2^{n-(1-\epsilon/2)}\right)\) algorithm.
\(3/2\)-approximation of the diameter: Randomly sample a vertex \(S\) by including each vertex w.p. \(1/\sqrt n\). Let \(d(u, S) = \min_{v \in S} d(u, v)\) and \(w = \arg \max d(u, S)\). Let \(T = \{v \mid d(w, v) < d(w, S)\}\). Run BFS from vertices in \(S\) and \(T\), and return the longest distance. We see that w.h.p. \(|S|, |T| = \widetilde{\mathcal O}(\sqrt n)\). Suppose the real diameter \(D = d(a, b) = 3h\). If there is a vertex \(u \in S\) and \(v \in \{a, b\}\) such that \(d(u, v) \le h\) or \(d(u, v) \ge 2h\) then the BFS of \(u\) can get a \(3/2\)-approximation. The remain case is that for all \(u \in S\), \(h < d(u, a), d(u, b) < 2h\). Thus \(d(w, S) > h\). Similarly we only need to consider the case that \(h < d(w, b) < 2h\). In this case consider the vertex \(y\) on the path from \(w\) to \(b\) with distance \(h\) from \(w\). We see that \(y \in T\) and \(d(y, b) < h \Rightarrow d(y, a) > 2h\), so we are done.
OV \(\Rightarrow\) diameter: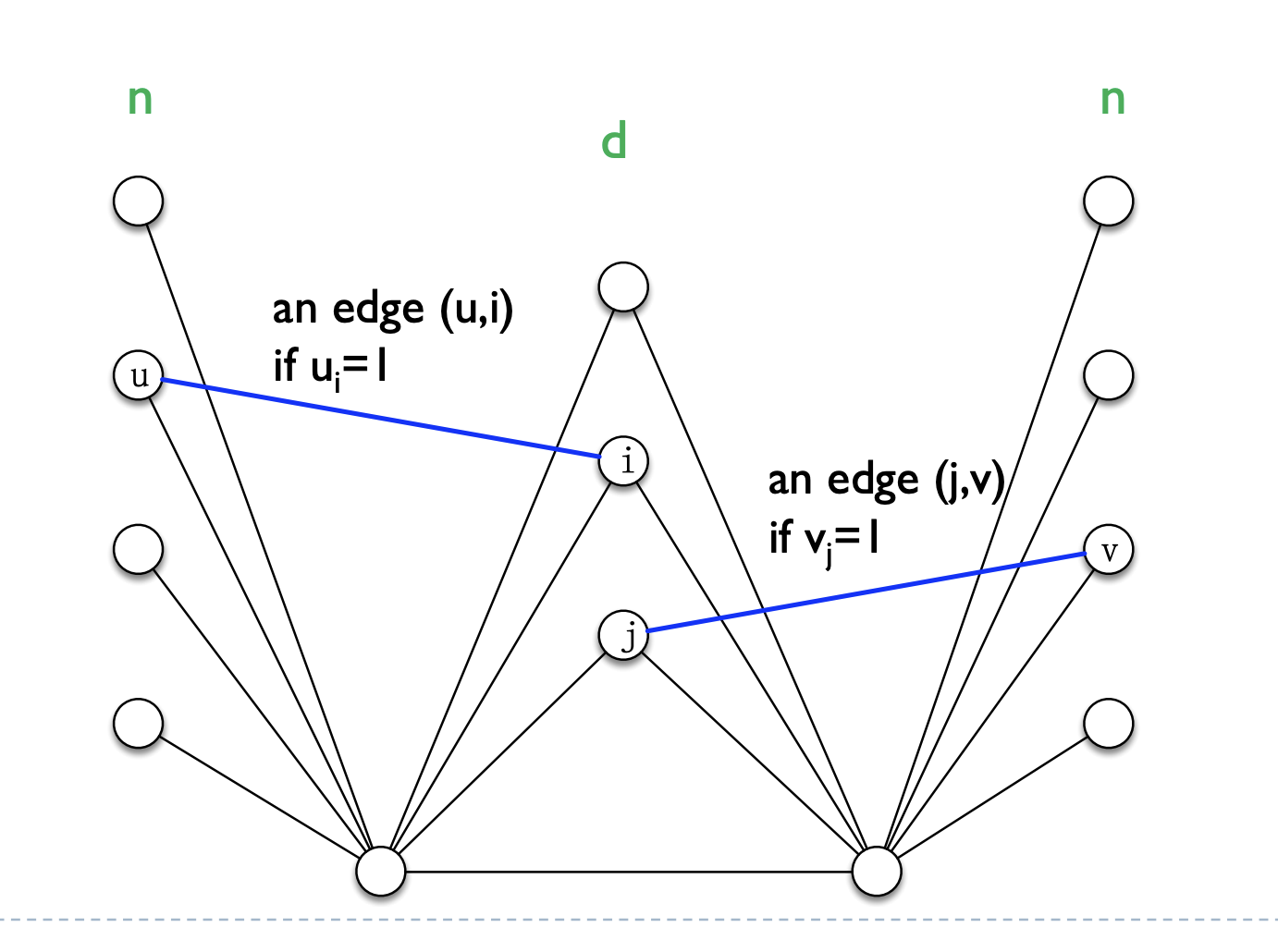 
We see that \(D = 3\) iff exists orthogonal vectors. Hence No \(\mathcal O(m^{2-\epsilon})\) time algorithm can compute the diameter better than \(3/2\)-approximation under OV conjecture.
OV \(\Rightarrow\) #SSR: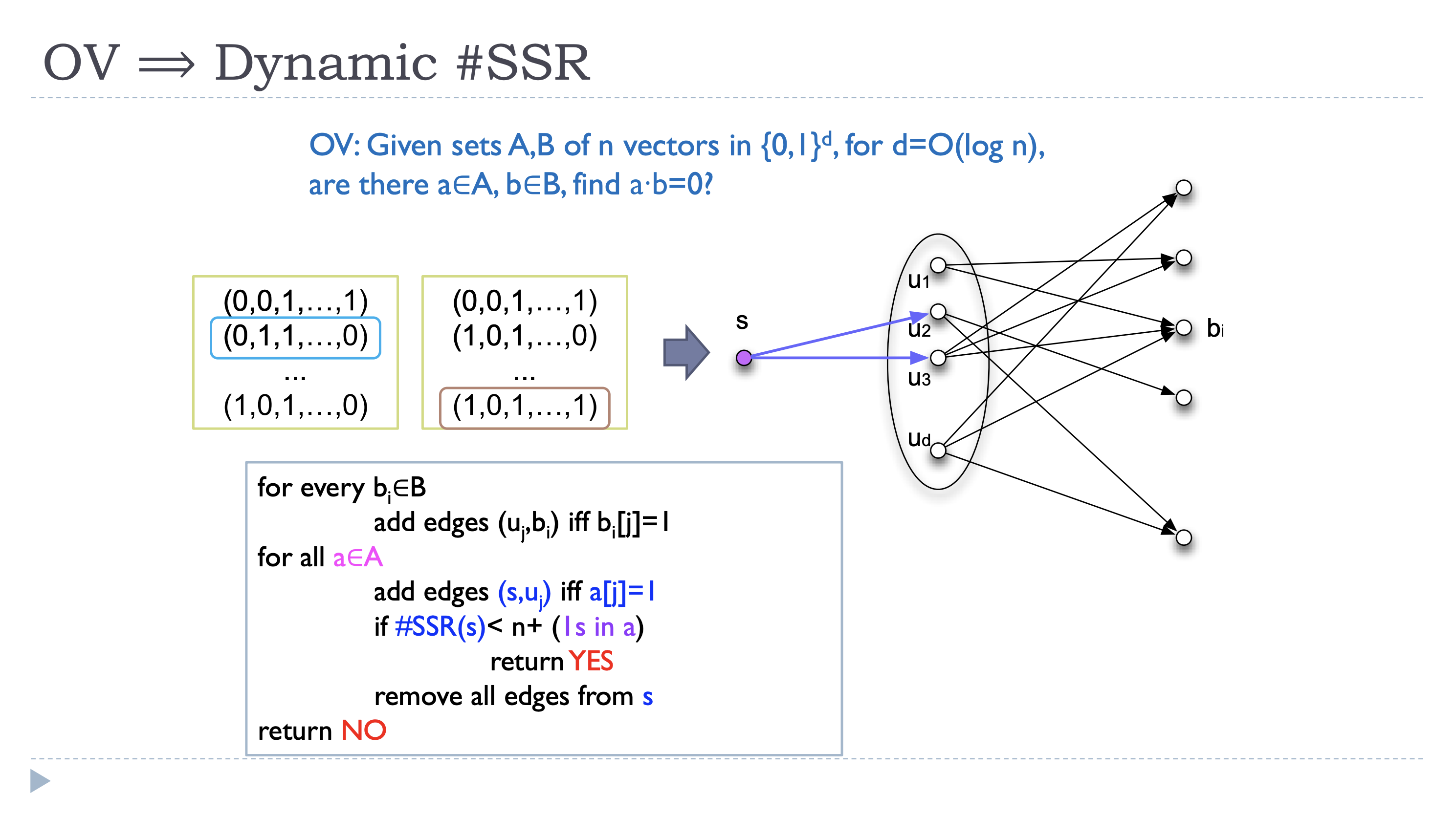 
浙公网安备 33010602011771号