OI 2012

目录

• OI 2012
  • 嘲讽对象
    • P3833 [SHOI2012]魔法树
  • NOI
    • P2179 [NOI2012] 骑行川藏
      • Problem
      • Hint
      • Solution
  • CTSC
  • 清华集训2012
    • P5933 [清华集训2012]串珠子
      • Problem
      • Solution
    • P4247 [清华集训2012]序列操作
      • Problem
      • Solution
  • HAOI
    • P2220 [HAOI2012]容易题
      • Problem
      • Solution
    • P2221 [HAOI2012]高速公路
      • Problem
      • Solution
  • TJOI
  • JSOI
    • P5232 [JSOI2012]智者的考验
      • Problem
      • Solution
    • P5233 [JSOI2012]爱之项链
  • SHOI
    • P3830 [SHOI2012]随机树
      • Problem
      • Solution
        • Problem 1
        • Problem 2
    • P3828 [SHOI2012]火柴游戏
      • Problem
      • Solution
  • SCOI
  • BJOI
    • P4133 [BJOI2012]最多的方案
      • Problem
      • Solution
  • JXOI
  • HNOI
  • HEOI
    • P4113 [HEOI2012]采花
      • Problem
      • Solution
    • P4598 [HEOI2012]Akai 的数学作业
      • Problem
      • Solution
  • JLOI
    • P3251 [JLOI2012]时间流逝
      • Problem
      • Solution
  • SDOI
    • P2351 [SDOI2012]吊灯
    • P2500 [SDOI2012]集合
      • Problem
      • Solution
  • CQOI
    • P3161 [CQOI2012]模拟工厂
      • Problem
      • Solution

OI 2012

嘲讽对象

P3833 [SHOI2012]魔法树

一道树剖板题放 D2T3，真是给 SHOI 丢脸。

NOI

P2179 [NOI2012] 骑行川藏

Problem

形式化题意：满足 \(\sum\limits_{i = 1}^{n}k_i(v_i - v_i^{'})^2s_i \le E_{U}\) 的条件下，最小化 \(\sum\limits_{i = 1}^{n}\frac{s_i}{v_i}\)。

对于 \(100\%\) 的数据，\(n\le 10^4\)，\(E_U\le 10^8\)，\(s_i\in(0,10^5]\)，\(k_i\in(0,15]\)，\(v_i'\in(-100,100)\)。

数据保证最终的答案不会超过 \(10^5\)。

Hint

必然存在一种最优的体力方案满足：蛋蛋在每段路上都采用匀速骑行的方式。

Solution

不妨就把能量和所求即时间关联起来。

\[E = ks(v - v^{'})^2 \\ t = \frac{s}{v} \]

把 \(E\) 看作自变量，\(t\) 看作因变量，我们希望 \(E\) 增大时，\(t\) 的变化率是足够大的。这玩意儿是导数啊。

链式法则一下得

\[\frac{dt}{dE} = - \frac{1}{2kv^2(v - v^{'})} \]

然后有个结论是：最优解时每段路程的 \(\frac{dt}{dE}\) 相等。否则我们可以去导数较大的那一段分配能量，性价比 更高。

假设最后这个导数为 \(x\)。则 \(x = -\frac{1}{2kv^2(v - v^{'})}\)。

当 \(v > v^{'}\) 时，\(x\) 为负数，函数单增。而 \(E = ks(v - v^{'})^2\)，即 \(v\) 越大时 \(E\) 越大，也即 \(x\) 越大 \(E\) 越大。二分 \(x\)，使 \(E\) 趋近于 \(E_{U}\)。很明显，能量用得越多，时间会越短。

枚举 \(x\) 后求 \(v\) 时也可以用二分解决。

有些细节不要短路了。要不然自己都觉得很鬼畜。（比如倒着走

慎用 int。

CTSC

• P4020 [CTSC2012]电阻网络

  物理竞赛

清华集训2012

P5933 [清华集训2012]串珠子

Problem

铭铭有 \(n\) 个十分漂亮的珠子和若干根颜色不同的绳子。现在铭铭想用绳子把所有的珠子连成一个整体。

现在已知所有的珠子互不相同，用整数 \(1\) 到 \(n\) 编号。对于第 \(i\) 个珠子和第 \(j\) 个珠子，可以选择不用绳子连接，或者在 \(c_{i,j}\) 根不同颜色的绳子中选择一根将它们连接。如果把珠子看作点，把绳子看作边，将所有珠子连成一个整体即为所有点构成一个连通图。特别地，珠子不能和自己连接。

铭铭希望知道总共有多少种不同的方案将所有珠子连成一个整体。由于答案可能很大，因此只需输出答案对 \(1000000007\) 取模的结果。

对于 \(100\%\) 的数据，\(n\) 为正整数，所有的 \(c_{i,j}\) 为非负整数且不超过 \(1000000007\)。保证 \(c_{i,j}=c_{j,i}\)。\(n \le 16\)。

Solution

不妨先思考一下 \(c_{i, j} = 1\) 的情况，即求 \(n\) 个点的无向连通图个数。

令 \(f_{i}\) 表示 \(i\) 个点的无向连通图个数，\(g_{i}\) 表示 \(i\) 个点的无向图个数，\(h_i\) 表示 \(i\) 个点的无向不连通图个数。则

\[g_i = 2^{\frac{n(n - 1)}{2}} \\ h_i = \sum\limits_{j = 1}^{i - 1}\binom{i - 1}{j - 1}\times f_{j}\times g_{i - j} \\ f_{i} = g_{i} - h_{i} \]

其中 \(h_i\) 的求法相当于枚举 \(1\) 所在连通块的大小。

本题中，由于不同的点对间能连的边的种数是不同的，又 \(n \le 16\)，考虑状压，枚举点集。

令 \(f_{S}\) 表示点集 \(S\) 的连通连边方案数，\(g_{S}\) 为 \(S\) 的总连边方案数，\(h_S\) 为 \(S\) 的不连通连边方案数。

用与上面类似的思想解决本问题：

\[g_{S} = \prod\limits_{i, j\in S}c_{i, j} + 1 \]

而 \(h_{S}\) 的转移思路为：任选一点 \(i \in S\)，令 \(T = S - \{i \}\)，然后枚举 \(T\) 的非空子集 \(S1\)，把 \(S1\) 关于 \(T\) 的补集 \(S2\) 并上 \(\{i \}\) 的结果作为 \(i\) 所在连通块的点集。即

\[h_S = \sum\limits_{S1 \subset T,S1 \neq \emptyset}g_{S1}\times f_{S2 \cup \{i \}} \]

直接像上面说的那样枚举肯定得死，并且是有可能计重的。不如把过程想得更简单点：就是要把点集分成两个部分，一部分钦定包含点 \(1\) 且连通，另一部分随意。就这样。

显然也有 \(f_{S} = g_{S} - h_{S}\)。

最终答案即为 \(f_{2^n - 1}\)。

P4247 [清华集训2012]序列操作

洛谷：P4247 [清华集训2012]序列操作

Problem

有一个长度为\(n\)的序列，有三个操作：

1. I a b c表示将\([a,b]\)这一段区间的元素集体增加\(c\)；
2. R a b表示将\([a,b]\)区间内所有元素变成相反数；
3. Q a b c表示询问\([a,b]\)这一段区间中选择\(c\)个数相乘的所有方案的和\(\mod 19940417\)的值。

Solution

P4247 [清华集训2012]序列操作 独立题解

观察数据范围，发现 \(c\le 20\)，提示我们此题可能有与 \(c\) 相关的复杂度的解法。

这道题的中心就在第三个操作，我们不妨先思考静态询问怎么做。

记 \(f[l][r][i]\) 表示 \([l,r]\) 内选 \(i\) 个数相乘的所有方案的和，则：

\[f[l][r][i] = \sum\limits_{k = 0}^{i}f[l][j][k]\times f[j + 1][r][i - k] \]

其中 \(j\) 可以为 任意 \([l, r]\) 内的位置。

既然如此，我们不妨令 \(j = mid\)，这不就很线段树了吗？

然后再考虑修改。

举一个最简单的例子 \(a_{1}a_{2} + a_{2}a_{3} + a_{1}a_{3} \to (a_{1} + val)(a_{2} + val) + (a_{2} + val)(a_{3} + val) + (a_{1} + val)(a_{3} + val)\) 来观察。

记新数列的答案为 \(f^{'}[l][r][i]\)，考虑如何用 \(f\) 更新 \(f^{'}\)。

发现新式可以视为一个关于 \(val\) 的 \(c\) 次多项式，我们不妨枚举 \(val\) 的次数，发现刚好可以凑出 \(f\)，即：

\[f^{'}[l][r][i] = \sum\limits_{k = 0}^{i}\left( \binom{len - i + k}{k}f[l][r][i - k] \right) val^{k} \]

这里 \(len = r - l + 1\)。

对于组合系数，可以理解为：

乘积项共 \(\binom{len}{i}\) 组，每组中的 \(val^{k}\) 项可由 \(\binom{i}{k}\) 个 \(\left( \prod\limits_{j = 1}^{i - k} a_{b_j} \right)val^{k}\) 的形式累加起来，而 \(f[l][r][i - k]\) 中已经蕴含了 \(\binom{len}{i - k}\) 种选法，所以系数应为

\[\frac{\binom{len}{i}\binom{i}{k}}{\binom{len}{i - k}} = \binom{len - i + k}{k}. \]

对于正负反转的操作，其实就是：

\[f^{'}[l][r][i] = f[l][r][i], i \equiv 1 \pmod{2} \]

注意先处理正负标记再处理加标记。

HAOI

P2220 [HAOI2012]容易题

Problem

有一个数列 \(A\) 已知对于所有的 \(A[i]\) 都是 \(1\sim n\) 的自然数，并且知道对于一些 \(A[i]\) 不能取哪些值，我们定义一个数列的积为该数列所有元素的乘积，要求你求出所有可能的数列的积的和 \(\bmod{10^9 + 7}\) 的值。

Solution

\(k = 0\) 时，\(ans = (\frac{n(n + 1)}{2})^m\)。

我们把每一个位置上的贡献记作 \(c_i\)，则上述记作 \(c_i = \frac{n(n + 1)}{2}, ans = \prod\limits_{i = 1}^{m}c_i\)。

有限制时，\(c_i = \frac{n(n + 1)}{2} - limit\)，其中 \(limit\) 表示所有被限制的数的和。

记被限制的位置有 \(cnt\) 个，这些特殊位置贡献的乘积为 \(w\)，则 \(ans = \prod\limits_{i = 1}^{m}c_i = w \times (\frac{n(n + 1)}{2})^{m - cnt}\)。

P2221 [HAOI2012]高速公路

Problem

给一条链，点依次编号为 \(1\sim n\)，支持区间线段增值，询问时给定 \(l, r\)，求在第 \(l\) 个到第 \(r\) 个点里等概率随机取出两个不同的点 \(a\) 和 \(b\)，从 \(a\) 走到 \(b\) 将期望花费多少费用。走的时候不能转向（题目貌似没说清楚？）。

Solution

注意两个方向都可以走QWQ

直接表达期望：

\[Ex(l, r) = \frac{\sum\limits_{i = l}^{r}\sum\limits_{j = l}^{r}d(i, j)}{\binom{r - l + 1}{2}} \]

发现问题在上面的式子，我们记为 \(S\)。很自然地想到对每一条线段统计贡献，可以得到

\[S = \sum\limits_{i = l}^{r - 1}v_i(i - l + 1)(r - i) \]

接下来的思路是，把式子拆出只与 \(v_i\) 相关的成分，而使其他部分可以 \(O(1)\) 得出。

\[\begin{aligned} S &= \sum\limits_{i = l}^{r - 1}v_i(ir - lr + r - i^2 + il - i) \\ &= \sum\limits_{i = l}^{r - 1}v_i[(r - lr) + (l + r - 1)i - i^2] \end{aligned} \]

记 \(s1 = \sum\limits_{i = l}^{r - 1}v_i, s2 = \sum\limits_{i = l}^{r - 1}i\times v_i, s3 = \sum\limits_{i = l}^{r - 1}i^2 \times v_i\)。则

\[S = (r - lr)s1 + (l + r - 1)s2 - s3 \]

于是用数据结构将三个和式分别维护。

TJOI

• P5193 [TJOI2012]炸弹

  曼哈顿距离转切比雪夫距离。早就听说过这个套路了，这次是第一次实践。然后扫描线。

  奇技淫巧：排序后每个点往后枚举 500 个点就能过

JSOI

P5232 [JSOI2012]智者的考验

Problem

原题目描述真是依托答辩。

形式化题意：给定目标状态。对于一个数列，支持单点覆盖，区间覆盖。每次询问时，给定 \(l, r\)，求 \(l\) 到 \(r\) 内有多少以 \(l\) 为始的前缀异或和与目标状态相同。

Solution

记 \(xrv_{i}\) 为 \(1\sim i\) 的前缀异或和。则对于询问 \(l, r\)，满足条件的一个单点 \(i\) 应满足 \(xrv_i \oplus xrv_{l - 1} = target \iff xrv_{i} = xrv_{l - 1} \oplus target\)。于是我们每次询问可以把右边的值 \(x\) 算出来，然后在 \(l\sim r\) 寻找有多少个值 \(x\)。

单点修改，

P5233 [JSOI2012]爱之项链

SHOI

P3830 [SHOI2012]随机树

Problem

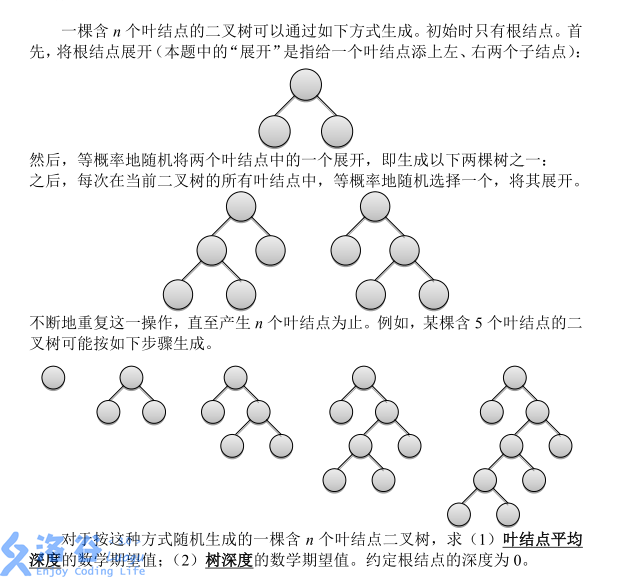
\(n \le 100\)。

Solution

Problem 1

记有 \(n\) 个叶节点时叶节点平均深度的期望值为 \(f_n\)。

\[\begin{aligned} f_{n} &= \frac{(n - 1)f_{n - 1} - f_{n - 1} + 2\times (f_{n - 1} + 1)}{n} \\ &= f_{n - 1} + \frac{2}{n} \end{aligned} \]

即：原来的叶节点期望深度和减去被展开点的期望深度加上新增点的期望深度再除以当前叶节点总数。

边界为 \(f_{1} = 0\)。

Problem 2

首先要对期望的公式足够熟悉。

\[E(x) = \sum\limits_{i = 1}^{+\infin}P(x \ge i) \]

记 \(f_{i, j}\) 表示有 \(i\) 个叶节点时，树的深度 \(\ge j\) 的概率。

\[f_{i, j} = \sum\limits_{k = 1}^{i - 1}\frac{1}{i - 1}(f_{k, j - 1} + f_{i - k, j - 1} - f_{k, j - 1}\times f_{i - k, j - 1}) \]

那么题解里面一堆人问为什么要除个 \(i - 1\)。我觉得不应该看为什么除以 \(i - 1\)，而该思考右边括号里的玩意儿加起来到底是什么，有什么含义？然后能看出左右子树叶节点数的分配在总数一定的情况下并不影响合起来合法的概率，这个 \(\frac{1}{i - 1}\) 就很显然了。

易知答案为

\[ans = \sum\limits_{i = 1}^{n - 1}f_{n, i} \]

边界 \(f_{i, 0} = 1\)。

P3828 [SHOI2012]火柴游戏

Problem

题目有点长。大概题意是：给两个长度相同的数字串，这些数字串都是用火柴拼出来的，可以通过删除，添加和移动火柴（均有不同的操作代价）使得两个数字串相等。求最小代价。

Solution

可以预处理出从一个数变换到另一个数至少要加多少根火柴以及删多少根火柴。

转移可以看作是删除和添加的结合，因此我们不妨先来看如何使只删除和添加时的代价尽可能小。

令 \(f_{i, j}\) 表示考虑前 \(i\) 个位置，添加了 \(j\) 根火柴后至少需要删多少根火柴。

\(f_{i, j} = \min(f_{i, j}, f_{i - 1, j - add} + del)\)。

其中 \(add\) 和 \(del\) 是通过枚举当前位置的数变为哪一个数字并结合预处理出的代价得到的操作次数。

然后再去枚举转移火柴的操作数，抵掉一组添加与删除。

那么这是我看到题解的做法。其实大致思路是对的，只是我们没有考虑一个问题：当添加的根数一定时，删除的根数真的越少越好吗？如果删除的根数稍微多一点，而让转移的次数变多，可能会使总代价更小。那怎么办呢？

在之前做过的某些 dp 题中，我们已经知道一个套路：以差值作为下标。

有的题中是为了降低复杂度，而这道题则是保证正确性。对于差值相等的两个删添组 \((i, j)\) 和 \((i + k, j + k)(k > 0)\)，这个无疑是删除次数越小越好了：因为 \((i, j)\) 包含于 \((i + k, j + k)\) 内。

SCOI

• P5038 [SCOI2012]奇怪的游戏

  二分，二分图，网络流，卡EK QWQ

BJOI

P4133 [BJOI2012]最多的方案

Problem

\[F_n = \begin{cases} 1 & (n \le 2) \\ F_{n-1}+F_{n-2} & (n \ge 3) \end{cases} \]

每一项都可以称为斐波那契数。

现在给一个正整数 \(n\)，它可以写成一些斐波那契数的和的形式。如果我们要求不同的方案中不能有相同的斐波那契数，那么对一个 \(n\) 最多可以写出多少种方案呢？

Solution

• 可以归纳证明任意正整数都能被分为一个或多个不相同的斐波那契数之和。

• 考虑对一个正整数贪心选取斐波那契数，可知这样的选取方案唯一且满足选取的斐波那契数不相邻。记被选取的第 \(i\) 个斐波那契数在原斐波那契数列中为第 \(pos_i\) 个数。

• 令 \(g_{i, 0/1}\) 表示将 \(1 \sim f_{pos_i}\) 这些元素变换后，恰好组成 \(\sum\limits_{j = 1}^{i}f_{pos_j}\) 的方案数。\(0/1\) 表示是否分解 \(f_{pos_i}\)。

• \[\begin{cases} g_{i, 1} = g_{i - 1, 1} + g_{i - 1, 0} \\ g_{i, 0} = g_{i - 1, 1}\times \frac{pos_i - pos_{i - 1} - 1}{2} + g_{i - 1, 0}\times \frac{pos_i - pos_{i - 1}}{2} \end{cases} \]
  \[\begin{cases} g_{1, 1} = 1 \\ g_{1, 0} = \frac{pos_1 - 1}{2} \end{cases} \]

这个题够妙，值得回味。

额，另，\(f_1\) 和 \(f_2\) 视作相同。

JXOI

• P6239 [JXOI2012]奇怪的道路

  状压，难

HNOI

• P3226 [HNOI2012]集合选数

  状压

HEOI

P4113 [HEOI2012]采花

Problem

可离线。查询区间出现次数大于 \(1\) 的颜色的种数。

Solution

数据结构典题，考虑维护前驱。

P4598 [HEOI2012]Akai 的数学作业

Problem

给出一个一元 \(n\) 次方程：

\[a_0 + a_1x + a_2x^2 +…+ a^nx^n= 0 \]

求此方程的所有有理数解。\(n \le 100\)。

Solution

因为要求解为有理数，所以设解为 \(x = \frac{p}{q}\)，\(p\) 与 \(q\) 互质。则

\[\begin{aligned} a_0 + a_1\frac{p}{q} + a_2\left(\frac{p}{q} \right)^2 + \cdots + a_n\left(\frac{p}{q} \right)^n &= 0 \\ \sum\limits_{i = 0}^{n}a_i p^{i} q^{n - i} &= 0 \\ a_0 q^n &\equiv 0 \pmod{p} \end{aligned} \]

由于 \(p,q\) 互质，所以 \(p | a_0\)。类似地转化，有 \(q | a_n\)。

把 \(a_0\) 和 \(a_n\) 的约数整出来暴力枚举 \(p,q\) 互质组判断是否可行就可以了。

注意 \(a_0 = 0\) 时，要往高位一直找到第一个 \(a_i \neq 0\) 的位置，同时在答案中加入 \(0\)。

注意质数组要同时考虑负数的情况。

注意整数的输出。

JLOI

P3251 [JLOI2012]时间流逝

Problem

给定 \(n\) 种价值不同的元素，你需要维护一个可重集（开始是空集）。每一步你有 \(p\) 的概率删除集合中一个价值最小的元素，如果当前是空集则这种情况概率为 \(0\)；否则你将等概率的获得一个元素，满足这个元素的价值不大于任何一个已经获得的元素的价值。求达到（或超过）给定的一个阈值 \(T\) 所需的期望步数。

Solution

设当前能量圈的集合为 \(S\)，且当前期望值为 \(f(S)\)。用期望的定义直接表示：

\[f(S) = 1 + pf(P) + \frac{1 - p}{|\operatorname{suc}S|}\sum\limits_{V\in \operatorname{suc}S}f(V) \]

注意 \(S\) 的前驱状态 \(P\) 是唯一的。分析 \(S\) 及其前驱后继，发现这个转移结构很像一棵树，且当前式子表现出来是 \(f(S)\) 同时受父节点 \(P\) 与众子节点的影响。

我们希望它能只受父节点的影响，这样就可以实现从上至下一对一转移。

假设 \(f(S) = k_Sf(P) + b_{S}\)。其中 \(k_S,b_S\) 是对每个 \(S\) 唯一的常数。

记 \(t = \frac{1 - p}{|\operatorname{suc}S|}\)。

\[f(S) = 1 + pf(P) + t\sum\limits_{V \in \operatorname{suc}S}(k_Vf(S) + b_V) \]

记 \(\sigma_{k}(S) = \sum\limits_{V \in \operatorname{suc}S}k_V, \sigma_{b}(S) = \sum\limits_{V \in \operatorname{suc}S}b_V\)。则

\[\begin{aligned} f(S) &= 1 + pf(P) + t\sigma_{k}(S)f(S) + t\sigma_{b}(S) \\ (1 - \sigma_{k}(S))f(S) &= pf(P) + 1 + t\sigma_{b}(S) \\ f(S) &= \frac{p}{1 - t\sigma_{k}(S)}f(P) + \frac{1 + t\sigma_{b}(S)}{1 - t\sigma_{k}(S)} \end{aligned} \]

dfs 的时候从大往小取，返回 pair 类型，答案即为根的时候的 \(b_S\)。

SDOI

P2351 [SDOI2012]吊灯

P2500 [SDOI2012]集合

Problem

给出 \(n\) 个点 \(m\) 条边的带权无向图（即每条无向边上都有一个权值），有3个集合A、B、C。一开始无向图中所有点都属于A集合，有如下9种操作：

MoveA x：表示将第x个点从所在集合中删除，并加入至A集合。

MoveB x：表示将第x个点从所在集合中删除，并加入至B集合。

MoveC x：表示将第x个点从所在集合中删除，并加入至C集合。

AskAA：询问两个端点都属于A集合的所有边中最小的权值是多少。

AskAB：询问两个端点分别属于A集合和B集合的所有边中最小的权值是多少。

AskAC：询问两个端点分别属于A集合和C集合的所有边中最小的权值是多少。

AskBB：询问两个端点都属于B集合的所有边中最小的权值是多少。

AskBC：询问两个端点分别属于B集合和C集合的所有边中最小的权值是多少。

AskCC：询问两个端点都属于C集合的所有边中最小的权值是多少。

Solution

毫无头绪，直接上根号分治。记 \(d_u\) 为点 \(u\) 的度数。

度数分治，把 \(d_u \ge \sqrt{n}\) 个的至多 \(\sqrt{n}\) 个点设为关键点。

非关键点时，开 \(6\) 个全局 set 维护 AA,AB,AC,BB,BC,CC 的情况。

关键点时，分别对每个关键点开 \(3\) 个 set 维护与它相连的三种颜色的边权情况。

修改非关键点时，暴力枚举它的所有边，若另一个点是非关键点，在全局 set 修改，否则对另一个点维护的 set 进行修改。

修改关键点时，枚举关键点与关键点之间的边，对另一个关键点进行修改。

复杂度 \(O(Q\sqrt{n}\log{m})\)。差不多 \(6\times 10^8\)。开 \(3s\) 有点危。

但是 暴力都能跑过去的 正解是 卡不掉 很难卡掉的，而且题目有特殊性质的保证。

CQOI

P3161 [CQOI2012]模拟工厂

Problem

有一个称为”模拟工厂“的游戏是这样的：在时刻0，工厂的生产力等于1。在每个时刻，你可以提高生产力或者生产商品。如果选择提高生产力，在下一个时刻时工厂的生产力加1；如果选择生产商品，则下一个时刻你所拥有的商品数量增加p，其中p是本时刻工厂的生产力。有n个订单，可以选择接受或者不接受。第i个订单(ti, gi, mi)要求在时刻ti给买家提供gi个商品，事成之后商品数量减少gi，而收入增加mi元。如果接受订单i，则必须恰好在时刻ti交易，不能早也不能晚。同一时刻可以接受多个订单，但每个订单只能被接受一次。要求最后的总收入最大。例如，如果一共有两个订单(5,1,8)和(7,15,3)，用如下策略是最优的：时刻0, 1, 2提高生产力（时刻3的生产力为4），然后在时刻3，4生产商品，则在时刻5时将拥有8个商品。此时接受第1个订单（还会剩下7个商品），并且在时刻5，6继续生产商品，则在时刻7时拥有7+4+4=15个商品，正好满足订单2。

Solution

二次方程判别式判可行性外层枚举接收订单方案暴力求解。