QOJ #3091. Japanese Knowledge 题解
Description
给定一个非递减的正整数序列 \(A = (A_1, A_2, \ldots, A_N)\)
对于每个 \(k = 0, 1, 2, \ldots, N\),要求计算满足以下条件的、长度为 \(N\) 的非递减非负整数序列 \(x = (x_1, x_2, \ldots, x_N)\) 的数量,并对结果取模 \(998244353\):
- 对所有 \(1 \leq i \leq N\),有 \(x_i \leq A_i\)。
- 恰好有 \(k\) 个下标 \(i\) 满足 \(x_i = A_i\)。
\(1\leq N,A_i\leq 2.5\times 10^5\)。
Solution
设 \(f_k(a_1,a_2,\ldots,a_n)\) 为有恰好 \(k\) 个 \(x_i=a_i\) 的方案数,\(g(a_1,a_2,\ldots,a_n)\) 为不考虑 \(x_i=a_i\) 这条限制的总方案数。
首先这题只有第一个限制是能做的,但是加上第二个限制就不好做了。所以考虑怎么把第二个限制去掉。
有个想法是对第二个进行容斥,但是会发现是不行的。于是需要找一些关于 \(x_i=a_i\) 的性质。
这里先给出结论:所有 \((a_{k+1}-1,a_{k+2}-1,\ldots,a_n-1)\) 的方案都一一对应了一个原序列有 \(k\) 个 \(x_i=a_i\) 的方案。
证明就考虑如果有恰好 \(k\) 个 \(x_i=a_i\),把这 \(k\) 个数去掉后的 \(x'_i\) 一定要小于 \(a_{i+k}\)。因为如果 \(x'_i\geq a_{i+k}\),则 \(a_{i+k}\leq x'_i\leq x_i\),这时 \(x_i,x_{i+1},\ldots,x_k\) 都必须顶到上界,就矛盾了。
对于一个满足 \(x'_i<a_{i+k}\) 的方案,考虑从小到大放到原数组中。每次一定是找到 \(x'_i<a_j\) 的最小的 \(j\) 放进去,如果不是最小的 \(j\),则最小的 \(k\) 一定会顶到上界,而 \(x'_i<a_k\),就矛盾了。由于已经满足了 \(x'_i<a_{i+k}\),所以这么操作一定能找到唯一的一组方案。
现在问题变为对于每个后缀,求 \(g(a_k-1,a_{k+1}-1,\ldots,a_n-1)\)。
考虑分治。
问题可以转化为有 \(n\) 个柱子,第 \(i\) 个柱子高 \(h_i=a_i-1\),问从最右侧每次往左或者往下走,有多少种走到 \((i,0)\) 的方案。
我们定义函数 \(solve(l,r,F)\) 为当前分治区间为 \([l,r]\),且这个区间内的每个柱子的高度都减去 \(h_{l-1}\),从 \(n\) 走到当前的 \((r,i)\) 的方案数为 \(F_i\);返回值为一个多项式 \(G\),其中 \(G_i\) 为走到 \(l+i\) 的方案数。
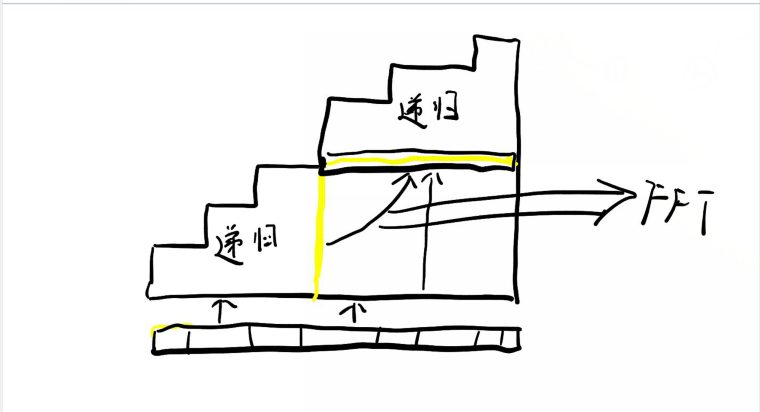
(图是贺的)
每次找到中点 \(mid\),然后调用 \(solve(mid+1,r,F)\),求出从最右边走到横着的黄线的每个位置的方案数,再通过 NTT 求出从横着的黄线走到竖黄线的每个位置的方案数 \(H\),最后调用 \(solve(l,mid,H)\)。
在分治的过程中,还要更新 \([mid+1,r]\) 终点在黄线下面的方案数,和上面的东西是类似的。
时间复杂度:\(O((N+V)\log^2 N)\)。
Code
#include <bits/stdc++.h>
// #define int int64_t
const int kMaxN = 5e5 + 5, kMod = 998244353;
int n;
int a[kMaxN], res[kMaxN], fac[kMaxN], ifac[kMaxN];
constexpr int qpow(int bs, int64_t idx = kMod - 2) {
int ret = 1;
for (; idx; idx >>= 1, bs = (int64_t)bs * bs % kMod)
if (idx & 1)
ret = (int64_t)ret * bs % kMod;
return ret;
}
inline int add(int x, int y) { return (x + y >= kMod ? x + y - kMod : x + y); }
inline int sub(int x, int y) { return (x >= y ? x - y : x - y + kMod); }
inline void inc(int &x, int y) { (x += y) >= kMod ? x -= kMod : x; }
inline void dec(int &x, int y) { (x -= y) < 0 ? x += kMod : x; }
namespace POLY {
constexpr int kMaxN = 4e6 + 5, kR = 3, kB = __builtin_ctz(kMod - 1), kG = qpow(kR, (kMod - 1) >> kB);
int polyg[kMaxN];
bool inited;
void prework(int n = (kMaxN - 5) / 2) {
inited = 1;
int c = 0;
for (; (1 << c) <= n; ++c) {}
c = std::min(c - 1, kB - 2);
polyg[0] = 1, polyg[1 << c] = qpow(kG, 1 << (kB - 2 - c));
for (int i = c; i; --i)
polyg[1 << i - 1] = (int64_t)polyg[1 << i] * polyg[1 << i] % kMod;
for (int i = 1; i < (1 << c); ++i)
polyg[i] = (int64_t)polyg[i & (i - 1)] * polyg[i & -i] % kMod;
}
int getlen(int n) {
int len = 1;
for (; len <= n; len <<= 1) {}
return len;
}
struct Poly : std::vector<int> {
using vector::vector;
using vector::operator [];
friend Poly operator -(Poly a) {
static Poly c;
c.resize(a.size());
for (int i = 0; i < c.size(); ++i)
c[i] = sub(0, c[i]);
return c;
}
friend Poly operator +(Poly a, Poly b) {
static Poly c;
c.resize(std::max(a.size(), b.size()));
for (int i = 0; i < c.size(); ++i)
c[i] = add((i < a.size() ? a[i] : 0), (i < b.size() ? b[i] : 0));
return c;
}
friend Poly operator -(Poly a, Poly b) {
static Poly c;
c.resize(std::max(a.size(), b.size()));
for (int i = 0; i < c.size(); ++i)
c[i] = sub((i < a.size() ? a[i] : 0), (i < b.size() ? b[i] : 0));
return c;
}
friend void dif(Poly &a, int len) {
if (a.size() < len) a.resize(len);
for (int l = len; l != 1; l >>= 1) {
int m = l / 2;
for (int i = 0, k = 0; i < len; i += l, ++k) {
for (int j = 0; j < m; ++j) {
int tmp = (int64_t)a[i + j + m] * polyg[k] % kMod;
a[i + j + m] = sub(a[i + j], tmp);
inc(a[i + j], tmp);
}
}
}
}
friend void dit(Poly &a, int len) {
if (a.size() < len) a.resize(len);
for (int l = 2; l <= len; l <<= 1) {
int m = l / 2;
for (int i = 0, k = 0; i < len; i += l, ++k) {
for (int j = 0; j < m; ++j) {
int tmp = a[i + j + m];
a[i + j + m] = (int64_t)sub(a[i + j], tmp) * polyg[k] % kMod;
inc(a[i + j], tmp);
}
}
}
int invl = qpow(len);
for (int i = 0; i < len; ++i)
a[i] = (int64_t)a[i] * invl % kMod;
std::reverse(a.begin() + 1, a.begin() + len);
}
friend Poly operator *(Poly a, Poly b) {
if (!inited) prework();
int n = a.size() + b.size() - 1, len = getlen(n);
a.resize(len), b.resize(len);
dif(a, len), dif(b, len);
for (int i = 0; i < len; ++i)
a[i] = (int64_t)a[i] * b[i] % kMod;
dit(a, len);
a.resize(n);
return a;
}
friend Poly operator *(Poly a, int b) {
static Poly c;
c = a;
for (auto &x : c) x = (int64_t)x * b % kMod;
return c;
}
friend Poly operator *(int a, Poly b) {
static Poly c;
c = b;
for (auto &x : c) x = (int64_t)x * a % kMod;
return c;
}
friend void operator *=(Poly &a, Poly b) {
if (!inited) prework();
int n = a.size() + b.size() - 1, len = getlen(n);
a.resize(len), b.resize(len);
dif(a, len), dif(b, len);
for (int i = 0; i < len; ++i)
a[i] = (int64_t)a[i] * b[i] % kMod;
dit(a, len);
a.resize(n);
}
friend Poly shift(Poly f, int d) {
if (d == 0) return f;
if ((int)f.size() + d < 0) return {};
Poly g((int)f.size() + d, 0);
for (int i = 0; i < g.size(); ++i)
if (i - d >= 0 && i - d < f.size())
g[i] = f[i - d];
return g;
}
};
} // namespace POLY
using POLY::Poly;
int C(int m, int n) {
if (m < n || m < 0 || n < 0) return 0;
return 1ll * fac[m] * ifac[n] % kMod * ifac[m - n] % kMod;
}
void prework(int n = 5e5) {
fac[0] = 1;
for (int i = 1; i <= n; ++i) fac[i] = 1ll * i * fac[i - 1] % kMod;
ifac[n] = qpow(fac[n]);
for (int i = n; i; --i) ifac[i - 1] = 1ll * i * ifac[i] % kMod;
}
Poly solve(int l, int r, Poly F) {
assert(F.size() == a[r] - a[l - 1] + 1);
if (l == r) {
int ret = 0;
for (auto x : F) inc(ret, x);
return {ret};
}
int mid = (l + r) >> 1, llen = mid - l + 1, rlen = r - mid, d = a[mid] - a[l - 1];
Poly f = solve(mid + 1, r, shift(F, -d));
Poly G(d + 1, 0);
G[d] = f[0];
Poly pf(rlen, 0), pg(d + rlen - 1, 0);
for (int i = 0; i <= rlen - 1; ++i) pf[i] = 1ll * f[rlen - 1 - i] * ifac[rlen - 1 - i] % kMod;
for (int i = 0; i <= d + rlen - 2; ++i) pg[i] = fac[i];
pf *= pg;
for (int i = 0; i <= d - 1; ++i)
if (d + rlen - 2 - i >= 0 && d + rlen - 2 - i < pf.size())
inc(G[i], 1ll * pf[d + rlen - 2 - i] * ifac[d - 1 - i] % kMod);
//
if (d) {
pf.clear(), pg.clear();
pf.resize(d, 0), pg.resize(d, 0);
for (int i = 0; i < d; ++i) pf[i] = F[d - 1 - i];
for (int i = 0; i < d; ++i) pg[i] = 1ll * fac[i + rlen - 1] * ifac[i] % kMod;
pf *= pg;
for (int i = 0; i <= d - 1; ++i) inc(G[i], 1ll * pf[d - 1 - i] * ifac[rlen - 1] % kMod);
}
Poly ff = f;
if (d) {
pf.clear(), pg.clear();
pf.resize(rlen, 0), pg.resize(rlen, 0);
for (int i = 0; i < rlen; ++i) pf[i] = f[rlen - 1 - i];
for (int i = 1; i < rlen; ++i) pg[i] = 1ll * fac[d - 1 + i] * ifac[i] % kMod;
pf *= pg;
for (int i = 0; i <= rlen - 1; ++i) inc(ff[i], 1ll * pf[rlen - 1 - i] * ifac[d - 1] % kMod);
}
if (d) {
pf.clear(), pg.clear();
pf.resize(d, 0), pg.resize(d + rlen - 1, 0);
for (int i = 0; i < d; ++i) pf[i] = 1ll * F[d - 1 - i] * ifac[d - 1 - i] % kMod;
for (int i = 0; i < d + rlen - 1; ++i) pg[i] = fac[i];
pf *= pg;
for (int i = 0; i <= rlen - 1; ++i)
if (d + rlen - 2 - i >= 0 && d + rlen - 2 - i < pf.size())
inc(ff[i], 1ll * pf[d + rlen - 2 - i] * ifac[rlen - 1 - i] % kMod);
}
assert(ff.size() == r - mid);
Poly g = solve(l, mid, G);
return g + shift(ff, g.size());
}
void dickdreamer() {
std::cin >> n; prework();
for (int i = 1; i <= n; ++i) std::cin >> a[i], --a[i];
auto res = solve(1, n, Poly(a[n] + 1, 1));
res.emplace_back(1);
for (auto x : res) std::cout << x << ' ';
}
int32_t main() {
#ifdef ORZXKR
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
std::ios::sync_with_stdio(0), std::cin.tie(0), std::cout.tie(0);
int T = 1;
// std::cin >> T;
while (T--) dickdreamer();
// std::cerr << 1.0 * clock() / CLOCKS_PER_SEC << "s\n";
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号