CF1025G Company Acquisitions 题解

Description

有 \(n\) 个初创公司。每个公司可以是活跃的或已被收购的。如果一个公司被收购了，说明它正好跟随一个活跃的公司。一个活跃的公司可以被任意多个已被收购的公司跟随。活跃的公司不能跟随其他公司。

以下过程会一直进行，直到只剩下一个活跃的公司。每次执行下列步骤需要恰好 1 天：

1. 随机等概率选出两个不同的活跃公司 \(A\) 和 \(B\)。
2. 掷一次公平的硬币，等概率地决定 \(A\) 收购 \(B\) 或 \(B\) 收购 \(A\)（即如果 \(A\) 收购 \(B\)，那么 \(B\) 的状态从活跃变为已被收购，并开始跟随 \(A\)）。
3. 当一个公司从活跃变为已被收购时，它之前所有已被收购的下属公司都会变为活跃状态。

例如，可能出现如下情形：假设 \(A\)、\(B\) 是活跃公司，\(C\)、\(D\)、\(E\) 是 \(A\) 的已被收购公司，\(F\)、\(G\) 是 \(B\) 的已被收购公司：

红色表示活跃公司。

如果 \(A\) 收购 \(B\)，则状态变为 \(A\)、\(F\)、\(G\) 是活跃公司，\(C\)、\(D\)、\(E\)、\(B\) 是 \(A\) 的已被收购公司，\(F\) 和 \(G\) 没有下属：

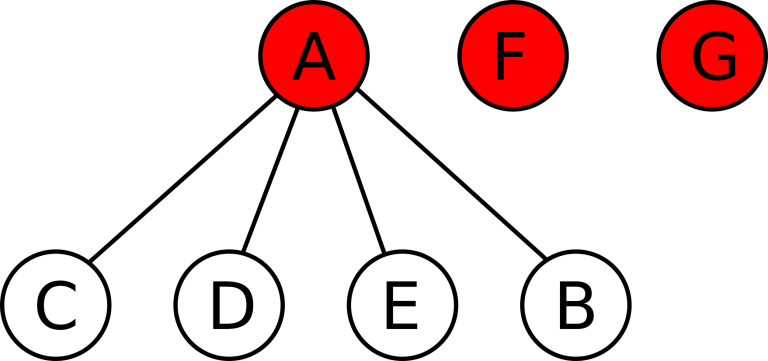
如果反过来 \(B\) 收购 \(A\)，则状态变为 \(B\)、\(C\)、\(D\)、\(E\) 是活跃公司，\(F\)、\(G\)、\(A\) 是 \(B\) 的已被收购公司，\(C\)、\(D\)、\(E\) 没有下属：

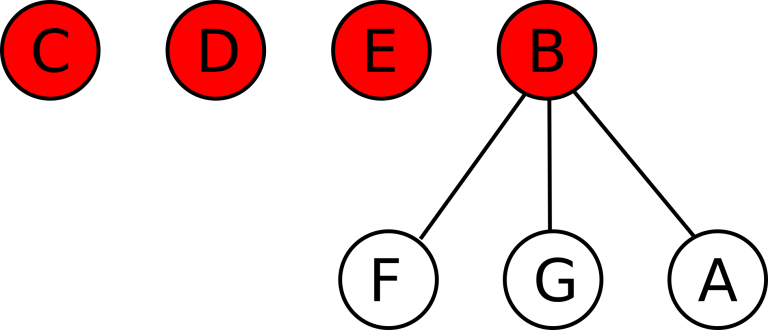
现在给定初创公司的初始状态。对于每个公司，告知其是活跃还是已被收购。如果是已被收购，还会给出它当前跟随的活跃公司的编号。

你需要计算，最终只剩下一个活跃公司时，所需天数的期望值。

可以证明，期望天数可以表示为有理数 \(P/Q\)，其中 \(P\) 和 \(Q\) 是互质整数，且 \(Q \not= 0 \pmod{10^9+7}\)。请输出 \(P \cdot Q^{-1}\) 模 \(10^9+7\) 的结果。

Solution

对于这类比较复杂的操作，问期望时间的问题有个技巧是用鞅与停时定理做。

具体地，设 \(f(x)\) 为一个固定函数，定义当前局面的权值是一个有关 \(f(x)\) 的确定组合，然后我们通过确定 \(f\) 来让每次操作后局面的期望权值总减少恰好 \(1\)，期望时间也就能用初始期望减去结束期望来算。

这题我们设 \(a_i\) 为第 \(i\) 个菊花的大小，定义一个局面的权值为 \(\sum f(a_i)\)，那么一次操作后权值的期望变化量为

\[\begin{aligned} \Delta=&\frac{1}{m(m-1)}\sum_{i=1}^{m}{\sum_{j\neq i}}{\left[f(a_i+1)+(a_j-1)f(1)-f(a_i)-f(a_j)\right]}\\ =&\frac{1}{m}\sum_{i=1}^{m}{\left[f(a_i+1)+(a_i-1)f(1)-2f(a_i)\right]}=-1\\ \end{aligned} \]

由于我们可以随意确定 \(f(x)\) 的值，所以这里让 \(f(1)=0\)，并让 \(f(a_i+1)-2f(a_i)\) 恒为 \(-1\) 即可满足等式的条件。也就是说 \(f(x)=2f(x-1)-1\)，初始条件是 \(f(1)=0\)。容易得到 \(f(x)=1-2^{x-1}\)。

最终答案为 \(\sum f(a_i)-f(n)\)，其中 \(a_i\) 为初始状态下第 \(i\) 个菊花的大小。

时间复杂度：\(O(n)\)。

Code

#include <bits/stdc++.h>

// #define int int64_t

const int kMaxN = 505, kMod = 1e9 + 7;

int n;
int cnt[kMaxN];

int qpow(int bs, int64_t idx = kMod - 2) {
  int ret = 1;
  for (; idx; idx >>= 1, bs = (int64_t)bs * bs % kMod)
    if (idx & 1)
      ret = (int64_t)ret * bs % kMod;
  return ret;
}

inline int add(int x, int y) { return (x + y >= kMod ? x + y - kMod : x + y); }
inline int sub(int x, int y) { return (x >= y ? x - y : x - y + kMod); }
inline void inc(int &x, int y) { (x += y) >= kMod ? x -= kMod : x; }
inline void dec(int &x, int y) { (x -= y) < 0 ? x += kMod : x; }

void dickdreamer() {
  std::cin >> n;
  for (int i = 1; i <= n; ++i) {
    int x;
    std::cin >> x;
    if (x == -1) ++cnt[i];
    else ++cnt[x];
  }
  int ans = 0;
  for (int i = 1; i <= n; ++i)
    if (cnt[i])
      inc(ans, sub(1, qpow(2, cnt[i] - 1)));
  dec(ans, sub(1, qpow(2, n - 1)));
  std::cout << ans << '\n';
}

int32_t main() {
#ifdef ORZXKR
  freopen("in.txt", "r", stdin);
  freopen("out.txt", "w", stdout);
#endif
  std::ios::sync_with_stdio(0), std::cin.tie(0), std::cout.tie(0);
  int T = 1;
  // std::cin >> T;
  while (T--) dickdreamer();
  // std::cerr << 1.0 * clock() / CLOCKS_PER_SEC << "s\n";
  return 0;
}