P6646 [CCO 2020] Shopping Plans 题解

Description

有 \(N\) 个商品，每个商品有个种类 \(a_i\)，有个价格 \(c_i\)。

对于第 \(j\) 个种类，必须购买个数位于 \([x_j,y_j]\) 的商品，即最少购买 \(x_j\) 个，最多购买 \(y_j\) 个该种类的商品。

您需要求出前 \(K\) 种便宜的方案所需的价钱，如果没有这样的方案，请输出 -1。

特别的，如果有相同钱数，但是具体方案不相同的，算作两种方案。

\(1\le N,M,K\le 2\times 10^5\)，\(1\le a_i\le M\)，\(1\le c_i\le 10^9\)，\(0\le x_j\le y_j\le N\)。

Solution

注：下面所有图片都来自这里。

首先考虑 \(m=1\) 且 \(x_1=y_1\) 怎么做。

先按照价格大小排序，容易发现最小的方案一定是前 \(x_1\) 小的这些数。

考虑用类似 dijkstra 的思想，维护一个堆表示当前可能有用的状态，每次选择堆里最优状态进行拓展。不过需要满足拓展方式不漏状态，且复杂度得对。

首先有个拓展方式是让当前最左边的能往右移的位置往右移若干位，且不碰到其它数。

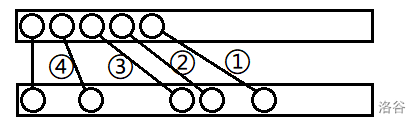
但是这么做单次需要拓展 \(O(n)\) 次，重复太多了。

不过可以让最左边能往右移的数只移动一个位置，这样就可以了。具体的操作如下：找到当前最左边且已经移动过的点 \(p\)，分两种：

1. 如果 \(p\) 右边没有数，就往右移动一步。
2. 让 \(p\leftarrow p-1\)，再让 \(p\) 往右移动一步。

正确性显然。

---

现在再考虑 \(m>1\) 且 \(x_i=y_i=1\) 的情况。

类似上面的做法，可以得到一个转移方式：记录 \(p\) 表示当前被移动过的最右边的种类，做如下操作：

1. 让 \(p\) 右移一步。
2. 找到一个 \(q>p\)，让 \(p\leftarrow q\)，再右移一步。

但是这么做单次转移还是 \(O(n)\) 的，考虑优化。

先按照次小值减最小值进行排序，记录 \(p\)，初始全选最小值，且 \(p=1\)，做如下操作：

1. 让 \(p\) 右移一步。
2. 如果 \(p\) 当前不是最小值，就把 \(p+1\) 设为次小值并让 \(p\leftarrow p+1\)。
3. 如果 \(p\) 当前是次小值，就让 \(p\) 变为最小值，\(p+1\) 变为次小值，并让 \(p\leftarrow p+1\)。

对于 \(x_i\neq 1\) 或者 \(y_i\neq 1\) 的情况，对每个种类维护一个黑盒，支持找到下一个状态即可，其余的操作和前面是一样的。

时间复杂度：\(O(n\log n)\)。

Code

#include <bits/stdc++.h>

#define int int64_t

const int kMaxN = 2e5 + 5;

int n, m, k, t;
int id[kMaxN], val[kMaxN];

struct Node {
  int n, L, R, now;
  std::vector<int> a, res = {0};
  std::priority_queue<std::tuple<int, int, int, int>, std::vector<std::tuple<int, int, int, int>>, std::greater<>> st;
  void init(int _L, int _R) {
    n = a.size(), a.emplace_back(0);
    L = _L, R = std::min(_R, n);
    std::sort(a.begin(), a.end());
    if (L > n) return;
    int x = L - 1, y = L, z = n + 1, sum = 0;
    for (int i = 1; i <= L; ++i) sum += a[i];
    st.emplace(sum, x, y, z);
  }
  int getnxt() {
    if (now + 1 < res.size()) {
      ++now;
      return res[now] - res[now - 1];
    }
    if (!st.size()) return 1e18;
    auto [sum, x, y, z] = st.top();
    st.pop();
    res.emplace_back(sum), ++now;
    if (y == x + 1 && z == n + 1 && y < R) st.emplace(sum + a[y + 1], x + 1, y + 1, z);
    if (y >= 1 && y + 1 < z) st.emplace(sum + a[y + 1] - a[y], x, y + 1, z);
    if (x >= 1 && x + 1 < y) st.emplace(sum + a[x + 1] - a[x], x - 1, x + 1, y);
    return res[now] - res[now - 1];
  }
  int getpre() { --now; return res[now] - res[now + 1]; }
} a[kMaxN];

void dickdreamer() {
  std::cin >> n >> m >> k;
  for (int i = 1; i <= n; ++i) {
    int x, c;
    std::cin >> x >> c;
    a[x].a.emplace_back(c);
  }
  int base = 0, sum = 0;
  for (int i = 1; i <= m; ++i) {
    int l, r;
    std::cin >> l >> r;
    a[i].init(l, r);
    if (r == 0) continue;
    if (a[i].n < l) {
      for (int j = 1; j <= k; ++j) std::cout << "-1\n";
      return;
    }
    // std::cerr << "!!! " << a[i].n << ' ' << l << ' ' << r << '\n';
    if (a[i].n == l) base += a[i].getnxt(), std::cerr << i << '\n';
    else sum += a[i].getnxt(), id[++t] = i, val[i] = a[i].getnxt();
    // std::cerr << "???\n";
  }
  std::sort(id + 1, id + 1 + t, [&] (int i, int j) { return val[i] < val[j]; });
  std::priority_queue<std::tuple<int, int, int>, std::vector<std::tuple<int, int, int>>, std::greater<>> q;
  for (int i = 1; i <= t; ++i) a[i].now = 1;
  q.emplace(sum, 1, 1);
  // std::cerr << sum << '\n';
  for (int i = 1; i <= k; ++i) {
    if (!q.size()) {
      std::cout << "-1\n";
      continue;
    }
    auto [sum, x, y] = q.top();
    q.pop();
    // std::cerr << "??? " << sum << ' ' << id[x] << ' ' << y << '\n';
    std::cout << sum + base << '\n';
    {
      a[id[x]].now = y;
      int det = a[id[x]].getnxt();
      if (det < 1e18) q.emplace(sum + det, x, y + 1);
    }
    if (x < t && y != 1) {
      a[id[x + 1]].now = 1;
      int det = a[id[x + 1]].getnxt();
      // std::cerr << "!!! " << det << '\n';
      if (det < 1e18) q.emplace(sum + det, x + 1, 2);
    }
    if (x < t && y == 2) {
      a[id[x]].now = y, a[id[x + 1]].now = 1;
      // std::cerr << "heige\n";
      int det = a[id[x]].getpre() + a[id[x + 1]].getnxt();
      // std::cerr << "nige\n";
      // std::cerr << "!!! " << det << '\n';
      if (det < 1e18) q.emplace(sum + det, x + 1, 2);
    }
  }
}

int32_t main() {
#ifdef ORZXKR
  freopen("in.txt", "r", stdin);
  freopen("out.txt", "w", stdout);
#endif
  std::ios::sync_with_stdio(0), std::cin.tie(0), std::cout.tie(0);
  int T = 1;
  // std::cin >> T;
  while (T--) dickdreamer();
  // std::cerr << 1.0 * clock() / CLOCKS_PER_SEC << "s\n";
  return 0;
}