[APC001G] Colorful Doors 题解

Description

有一座桥，上面有 \(2N\) 个传送门。这 \(2N\) 个传送门分成 \(N\) 组，每组恰好两个。我们用 \(1\) 到 \(N\) 的数字来区分每组传送门。

你从最左边进入这座桥，沿着朝右的方向一直走，每次碰到一个传送门，你会传送到它对应的传送门的位置，然后继续往右，直到走到第 \(2N\) 个传送门右边为止。可以证明在这个问题中，我们一定能走到第 \(2N\) 个传送门右边。

比如 6 个门，依次为 \(1, 3, 2, 1, 2, 3\)，用 \(1\) 到 \(6\) 表示这些门的标号。那么你行走的路径为 \(1 \hookrightarrow 4 \rightarrow 5 \hookrightarrow 3 \rightarrow 4 \hookrightarrow 1 \rightarrow 2 \hookrightarrow 6\)。其中 \(\hookrightarrow\) 表示传送，\(\rightarrow\) 表示行走。

现在你忘了传送门的具体对应关系，只记得对于每一段 \(i \to i+1\) 你是否经过。问能不能是否存在一种合法的传送门的方案，如果存在的话，构造一组解。

\(N\leq 10^5\)。

Solution

首先设 \(a_i\) 表示 \((i-1)\to i\) 是否经过，那么先把 \(a_1\) 和 \(a_{2n+1}\) 设为 \(1\)，即可以把走的过程看成一个环。

对于每个传送门，如果其左右的路都是 \(1\)，则将其看成 M，只有左边是 \(1\) 看成 S，只有右边是 \(1\) 看成 T。

那么没有标记的传送门一定不会经过，这些门可以随便填。其余的一定会经过。

注意到 M 门需要向右经过一次和传送一次，S 门只能向右，T 只能传送经过，所以 M 只能和 M 自己匹配，而 S 只能和 T 匹配。

所以如果 M 的个数为偶数，则一定无解。

---

考虑没有 S 和 T 的情况。

如果 M 的个数是 \(4\) 的倍数，可以如下构造：\([1,2,1,2,3,4,3,4,\ldots,2n-1,2n,2n-1,2n]\)。

如果模 \(4\) 余 \(2\) 则一定无解。

---

现在考虑上 S 和 T。

首先如果 M 的个数是 \(4\) 的倍数，按照上面的方式把所有 M 的位置拿出来匹配，对于相邻的 ST 匹配在一起，经过手玩仍然是对的。具体可以看这个图（从这里拿的，侵删）

如果 \(M\) 的个数模 \(4\) 余 \(2\)，上面就不能直接做了。但是注意到上面的做法很强，在中间随便加入一些东西仍然是对的，所以考虑选择两个 M 进行匹配，并达到等效删除的作用。

考虑下面这种情况：

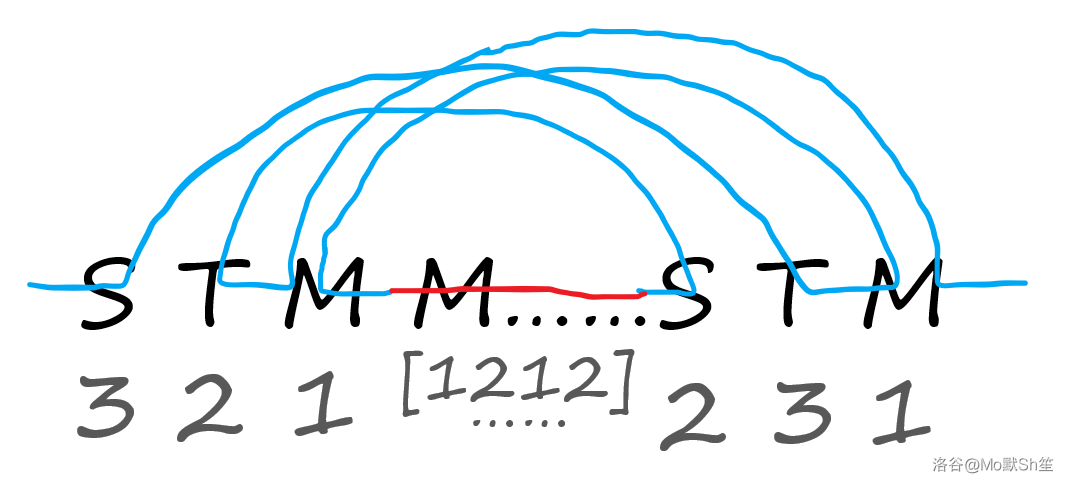
将相邻的 M 极长段拿出来，如果前面的段被两个 ST 包围，则可以分别将两段第一个的 M 匹配，同时第一个 ST 的 T 和第二个 ST 的 S 也进行匹配。

其余的不变，手玩可发现这么做对于其余的结构相当于是在其中嵌入一部分数。要想这东西大概是注意到前面将相邻 ST 匹配，如果不匹配一个 TS 就一定不会走出回头路把这两个数删掉。现在先作出一个 TS，然后显然要跨段，可以猜到是将两段分别第一个 M 进行匹配。

还有一种情况是这个：

和上面对称，容易证明如果找不到这样的两个段就一定不合法，因为这样的状态就一定长成 MMMSTMMM 的形式，还是通过手玩可以知道其不合法。

对于剩下没有匹配的位置，直接把这些位置拿出来做 M 模 \(4\) 为 \(0\) 的做法即可。

时间复杂度：\(O(n)\)。

Code

#include <bits/stdc++.h>

// #define int int64_t

const int kMaxN = 2e5 + 5;

int n, m, cnt;
int a[kMaxN], op[kMaxN], id[kMaxN], res[kMaxN];
std::string s;

void add(int x, int y) {
  assert(!res[x] && !res[y]);
  res[x] = res[y] = ++cnt;
}

void dickdreamer() {
  std::cin >> n >> s; m = cnt = 0;
  a[1] = a[2 * n + 1] = 1;
  for (int i = 1; i <= 2 * n; ++i) res[i] = 0;
  for (int i = 2; i <= 2 * n; ++i) a[i] = s[i - 2] - '0';
  int cntM = 0;
  op[0] = op[2 * n + 1] = 0;
  for (int i = 1; i <= 2 * n; ++i) {
    if (!a[i] && a[i + 1]) op[i] = 1; // T
    else if (a[i] && !a[i + 1]) op[i] = 2; // S
    else if (a[i] && a[i + 1]) op[i] = 3, ++cntM; // M
    else op[i] = 0;
    // std::cerr << op[i] << ' ';
  }
  // std::cerr << '\n';
  if (cntM & 1) return void(std::cout << "No\n");
  if (cntM % 4 == 2) {
    int lstl = 0, lstr = 0;
    bool fl = 0;
    for (int l = 1, r = 1; l <= 2 * n; l = r + 1) {
      for (; l <= 2 * n && op[l] != 3; ++l) {}
      if (l > 2 * n) break;
      r = l;
      for (; r < 2 * n && op[r + 1] == 3; ++r) {}
      // std::cerr << "??? " << l << ' ' << r << '\n';
      if (lstl && lstr) {
        if (op[l - 1] == 1 && op[r + 1] == 2) {
          add(lstr, r), add(l - 1, r + 1), fl = 1;
        } else if (op[lstl - 1] == 1 && op[lstr + 1] == 2) {
          add(lstl, l), add(lstl - 1, lstr + 1), fl = 1;
        }
      }
      lstl = l, lstr = r;
      if (fl) break;
    }
    if (!fl) return void(std::cout << "No\n");
  }
  for (int i = 1; i <= 2 * n; ++i)
    if (!res[i] && op[i] == 3)
      id[++m] = i;
  assert(m % 4 == 0);
  for (int i = 1; i <= m; i += 4)
    add(id[i], id[i + 2]), add(id[i + 1], id[i + 3]);
  int lst[3] = {0};
  for (int i = 1; i <= 2 * n; ++i) {
    if (!res[i]) {
      // std::cerr << op[i] << '\n';
      if (op[i] == 0) {
        if (lst[0]) add(lst[0], i), lst[0] = 0;
        else lst[0] = i;
      } else if (op[i] == 1) {
        if (lst[2]) add(lst[2], i), lst[2] = 0;
        else lst[1] = i;
      } else {
        assert(op[i] == 2);
        if (lst[1]) add(lst[1], i), lst[1] = 0;
        else lst[2] = i;
      }
    }
  }
  std::cout << "Yes\n";
  for (int i = 1; i <= 2 * n; ++i) std::cout << res[i] << " \n"[i == 2 * n];
}

int32_t main() {
#ifdef ORZXKR
  freopen("in.txt", "r", stdin);
  freopen("out.txt", "w", stdout);
#endif
  std::ios::sync_with_stdio(0), std::cin.tie(0), std::cout.tie(0);
  int cid, T = 1;
  std::cin >> T >> cid;
  while (T--) dickdreamer();
  // std::cerr << 1.0 * clock() / CLOCKS_PER_SEC << "s\n";
  return 0;
}