[AGC047F] Rooks 题解

Description

有 \(N\) 个车在一张无限大的棋盘上，第 \(i\) 个在 \((X_i,Y_i)\)。每行每列最多一个车。

有一个卒，会替换第 \(s\) 个车，可以走八连通，但是不能走到被车攻击的地方。吃车的时候可以走对角，否则只能走上下左右。

对于 \(s=1\ldots N\)，求出吃掉最多的车时的最小步数。

\(2\leq N\leq 2\times 10^5,1\leq X_i,Y_i\leq 10^6,X_i\neq X_j,Y_i\neq Y_j\)。

Solution

先对 \(x,y\) 分别离散化并按照 \(x\) 坐标从小到大排序，那么 \(s\) 任何时刻吃的车一定构成一个区间 \([l,r]\)，满足 \(l\leq s\leq r\)。

显然可以进行 dp。

设 \(f_{l,r,0/1}\) 表示当前吃掉的车为 \([l,r]\)，且当前的位置是 \(l/r\)，到最终状态的最小步数。

容易发现任意时刻吃掉车的 \(y\) 坐标也构成一个区间 \([l_y,r_y]\)，所以下一步走的车坐标一定为 \((l-1,l_y-1),(l-1,r_y+1),(r+1,l_y-1),(r+1,r_y+1)\)。具体的，如果 \(y_{l-1}=l_y-1\)，可以得到转移方程：\(f_{l,r,0}\leftarrow f_{l-1,r,0}+\text{dis}(l-1,l)-1\)，剩下的同理。

这个做法的时间复杂度是 \(O(n^2)\)，过不了。

---

注意到这个做法的转移是 \(O(1)\) 的，而状态很多，所以考虑优化状态。

首先对于 \(y_i=i\) 的问题，一定是先从 \(s\) 走到 \(1\) 再走到 \(n\)，或者先到 \(n\) 再一路到 \(1\)。

这里也是一样的，如果先走到 \(l-1\) 且 \(|y_{l-2}-y_{l-1}|=1\)，那么一路向左走直到差不是 \(1\) 了一定更优。

考虑把这些相邻差为 \(1\) 的段缩起来，容易发现到达段内的任何一个点后段里的其它点也可以走过去。并且如果第一次到了这个段的左右端点，则之后一路把整段走完一定最优。

所以每次拓展时按照整段拓展即可，可以发现现在状态数减少了不少，实际状态上变成 \(O(n)\) 的了。

证明就考虑有用的状态一定满足区间内 \(y\) 构成一段区间且不能拓展，形如下面的图（图源：link）：

然后对于每个 \(y\) 相差 \(1\) 的极长连续段 \([l,r]\)，计算有多少个状态满足最后一次是从它拓展的。

由于 \([l,r]\) 极长，所以只有两种包含它的方案：

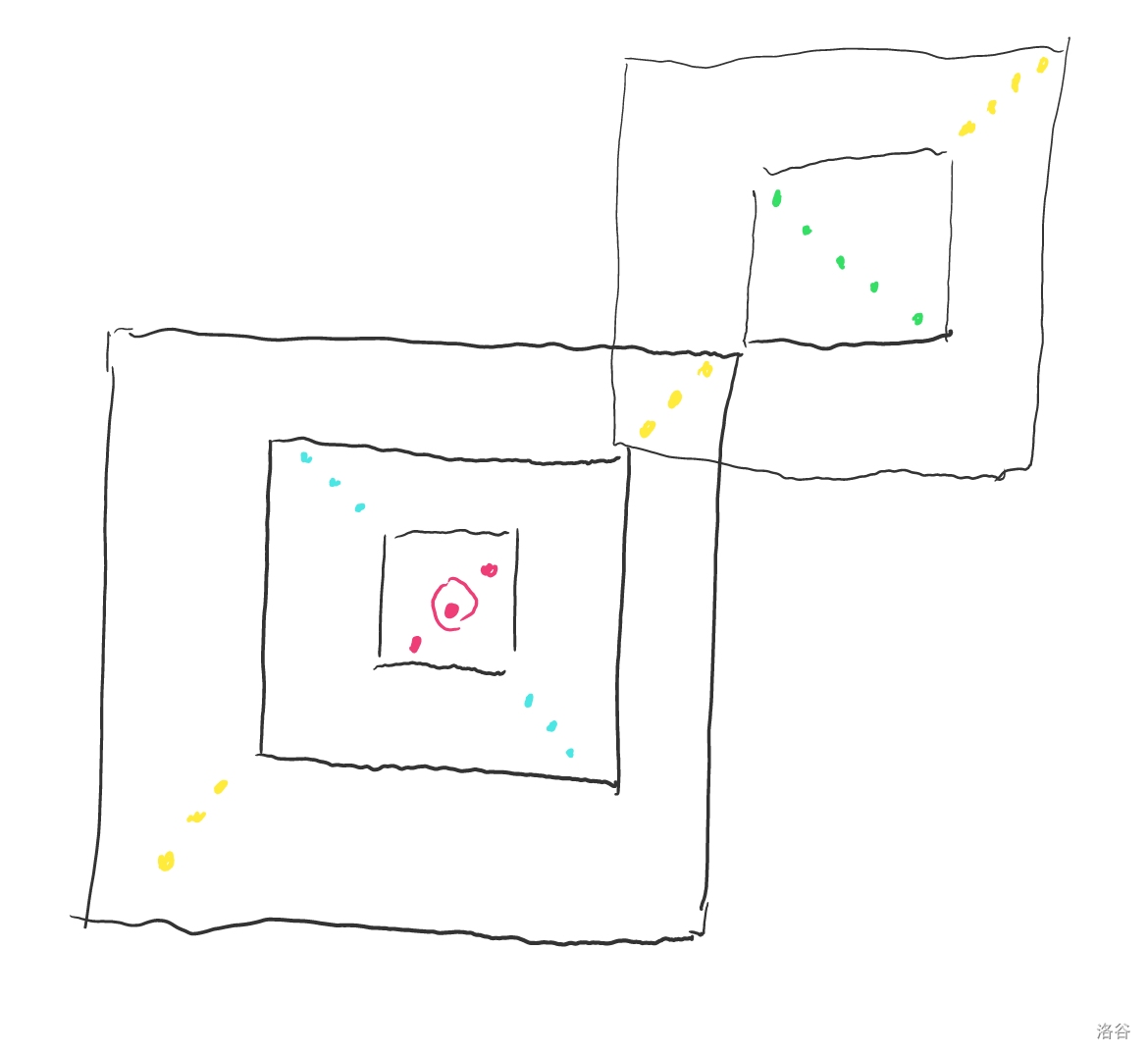
所以总状态数是 \(O(n)\) 的。

用一个哈希表存下这些状态即可。

时间复杂度：\(O(n\log n)\)。

Code

#include <bits/stdc++.h>

#define int int64_t

const int kMaxN = 2e5 + 5;

struct custom_hash {
  static uint64_t splitmix64(uint64_t x) {
    x += 0x9e3779b97f4a7c15;
    x = (x ^ (x >> 30)) * 0xbf58476d1ce4e5b9;
    x = (x ^ (x >> 27)) * 0x94d049bb133111eb;
    return x ^ (x >> 31);
  }
  size_t operator()(uint64_t x) const {
    static const uint64_t FIXED_RANDOM = std::chrono::steady_clock::now().time_since_epoch().count();
    return splitmix64(x + FIXED_RANDOM);
  }
  size_t operator()(std::tuple<uint64_t, uint64_t, uint64_t> x) const {
    static const uint64_t FIXED_RANDOM = std::chrono::steady_clock::now().time_since_epoch().count();
    return splitmix64(std::get<0>(x) + FIXED_RANDOM) ^
           (splitmix64(std::get<1>(x) + FIXED_RANDOM) >> 1) ^
           (splitmix64(std::get<2>(x) + FIXED_RANDOM) >> 2);
  }
};

int n;
int x[kMaxN], y[kMaxN], unqx[kMaxN], unqy[kMaxN], ans[kMaxN];
int L[kMaxN], R[kMaxN];
std::unordered_map<std::tuple<int, int, bool>, int, custom_hash> f;

struct Node {
  int x, y, id;
} t[kMaxN];

int getdis(int i, int j) {
  return abs(unqx[t[i].x] - unqx[t[j].x]) + abs(unqy[t[i].y] - unqy[t[j].y]);
}

int solve(int l, int r, int ly, int ry, bool isleft) {
  if (f.count({l, r, isleft})) return f[{l, r, isleft}];
  int ret = 1e18;
  if (l > 1 && (t[l - 1].y == ly - 1 || t[l - 1].y == ry + 1))
    ret = std::min(ret, solve(L[l - 1], r, std::min({ly, t[l - 1].y, t[L[l - 1]].y}), std::max({ry, t[l - 1].y, t[L[l - 1]].y}), 1) + getdis(l - 1, isleft ? l : r) + getdis(l - 1, L[l - 1]));
  if (r < n && (t[r + 1].y == ly - 1 || t[r + 1].y == ry + 1))
    ret = std::min(ret, solve(l, R[r + 1], std::min({ly, t[r + 1].y, t[R[r + 1]].y}), std::max({ry, t[r + 1].y, t[R[r + 1]].y}), 0) + getdis(r + 1, isleft ? l : r) + getdis(r + 1, R[r + 1]));
  if (ret == 1e18) ret = -(r - l);
  return f[{l, r, isleft}] = ret;
}

void dickdreamer() {
  std::cin >> n;
  for (int i = 1; i <= n; ++i) {
    std::cin >> x[i] >> y[i];
    unqx[i] = x[i], unqy[i] = y[i];
  }
  std::sort(unqx + 1, unqx + 1 + n);
  std::sort(unqy + 1, unqy + 1 + n);
  for (int i = 1; i <= n; ++i) {
    x[i] = std::lower_bound(unqx + 1, unqx + 1 + n, x[i]) - unqx;
    y[i] = std::lower_bound(unqy + 1, unqy + 1 + n, y[i]) - unqy;
    t[i] = {x[i], y[i], i};
  }
  std::sort(t + 1, t + 1 + n, [&] (auto a, auto b) { return a.x < b.x; });
  for (int i = 1; i <= n; ++i) {
    if (i > 1 && abs(t[i].y - t[i - 1].y) == 1) L[i] = L[i - 1];
    else L[i] = i;
  }
  for (int i = n; i; --i) {
    if (i < n && abs(t[i].y - t[i + 1].y) == 1) R[i] = R[i + 1];
    else R[i] = i;
  }
  for (int i = 1; i <= n; ++i) ans[t[i].id] = solve(i, i, t[i].y, t[i].y, 1);
  for (int i = 1; i <= n; ++i) std::cout << ans[i] << '\n';
}

int32_t main() {
#ifdef ORZXKR
  freopen("in.txt", "r", stdin);
  freopen("out.txt", "w", stdout);
#endif
  std::ios::sync_with_stdio(0), std::cin.tie(0), std::cout.tie(0);
  int T = 1;
  // std::cin >> T;
  while (T--) dickdreamer();
  // std::cerr << 1.0 * clock() / CLOCKS_PER_SEC << "s\n";
  return 0;
}