[ARC196B] Torus Loop 题解

Description

问题陈述

有一个由 \(H\) 行和 \(W\) 列组成的网格。行的编号从上到下为 \(0,1,\ldots,H-1\) ，列的编号从左到右为 \(0,1,\ldots,W-1\) 。让 \((i,j)\) 表示位于第 \(i\) 行和第 \(j\) 列的单元格。

给你 \(H\) 个字符串 \(S_0,S_1,\ldots,S_{n-1}\) ，每个字符串的长度为 \(W\) ，由 A 和 B 组成。

每个单元格中都放置了以下两种瓦片中的一种。让 \(S_{ij}\) 表示字符串 \(S_i\) 中的 \((j+1)\) -th 字符 \((0 \le j \le W-1)\) 。放置在 \((i,j)\) 单元格中的瓦片类型是 \(S_{ij}\) 。

• 类型 A：在磁砖表面绘制一条线段，连接相邻两条边的中点。

• 类型 B：在瓷砖表面绘制一条线段，连接两条相对边缘的中点。

这些瓷砖可以自由旋转。如果只关注线段形成的图案，A 型瓷砖有四种旋转方式，B 型瓷砖有两种旋转方式。因此，如果我们只根据线段图案来区分瓷砖的摆放位置，那么摆放瓷砖的方法数为 \(4^a \times 2^b\) ，其中 \(a\) 是A型瓷砖的数量， \(b\) 是B型瓷砖的数量。

在这些方法中，请打印出在将网格视为环形时，瓷砖上的线段没有死角的方法的数目，模数为 \(998244353\) 。

这里的 "将网格视为环形时，瓦片上的线段没有死角 "是指且仅当每个单元格 \((i,j)\) 满足以下两个条件时：

• 以下两个条件都存在，或者以下两个条件都不存在：
  • 在单元格 \((i,j)\) 中绘制的线段，其端点是单元格 \((i,j)\) 右边缘的中点
  • 在单元格 \((i,(j+1)\bmod W)\) 中绘制的线段，其端点是单元格 \((i,(j+1)\bmod W)\) 左边缘的中点
• 以下两项都存在，或者以下两项都不存在：
  • 在单元格 \((i,j)\) 中绘制的线段，其端点是单元格 \((i,j)\) 底边的中点
  • 在单元格 \(((i+1)\bmod H,j)\) 中绘制的线段，其端点是单元格 \(((i+1)\bmod H,j)\) 顶部边缘的中点

例如，下面的布局符合条件：

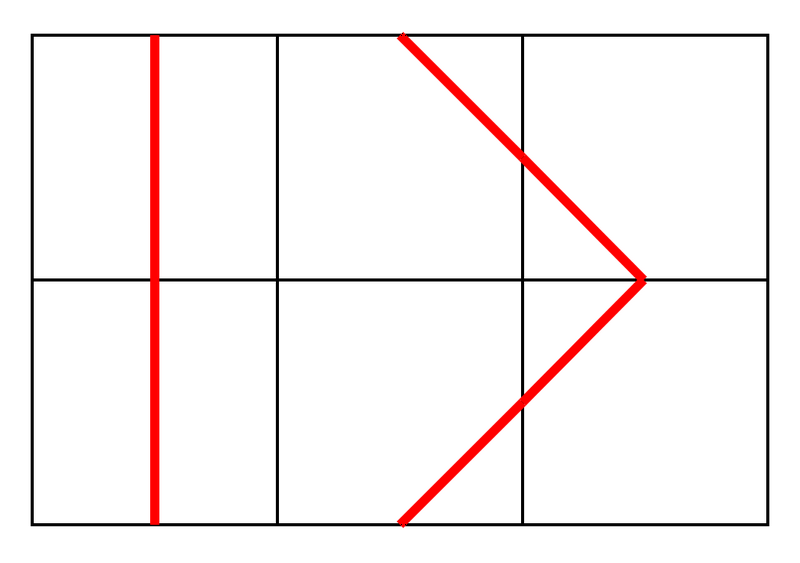
以下位置不符合条件。具体来说，虽然单元格 \((1,3)\) 中没有端点为磁贴右边缘中点的线段，但单元格 \((1,1)\) 中有端点为磁贴左边缘中点的线段，因此不满足条件。

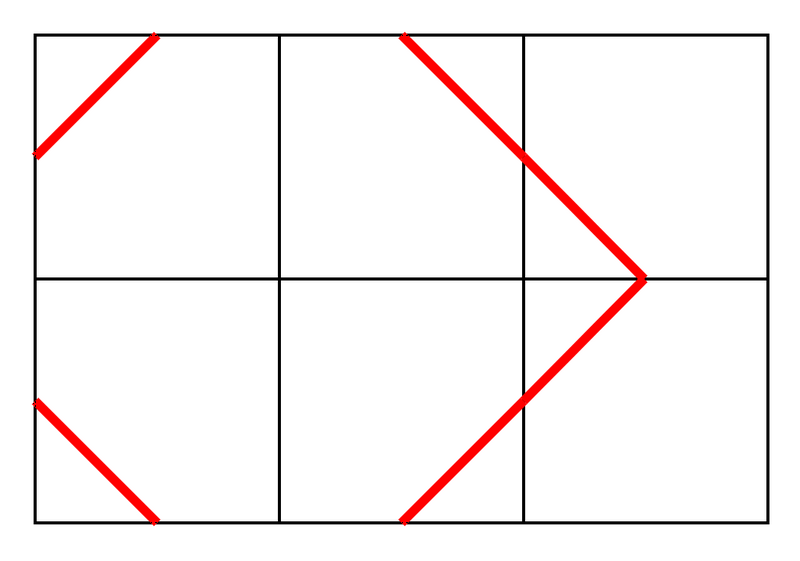
给您 \(T\) 个测试用例，请逐一求解。

\(HW\leq 10^6\)。

Solution

这里对每条边上是否有端点去考虑。

不妨设 \(C_{i,j}\) 表示 \((i,j)\) 格子左边的边是否有端点，\(D_{i,j}\) 表示 \((i,j)\) 上方的边是否有端点。

可以发现如果知道 \(C_{i,0}\) 的话，\(C_{i,1},C_{i,2},\ldots,C_{i,W-1}\) 也会确定。因为如果 \(S_{i,j}=\texttt{A}\)，则 \(C_{i,j+1}=1-C_{i,j}\)，否则 \(C_{i,j+1}=C_{i,j}\)。

所以知道每行每列第一条边的状态后整张图就确定了。

但是有些状态是不合法的，因为需要满足当 \(S_{i,j}=\texttt{B}\) 时，\(C_{i,j}\neq D_{i,j}\)。

这是一个形如第 \(i\) 行和第 \(j\) 列相等/不等的限制，连边后如果有解，答案就是 \(2\) 的连通块数量次方，否则答案是 \(0\)。

时间复杂度：\(O(HW)\)。

Code

#include <bits/stdc++.h>

// #define int int64_t

const int kMaxN = 1e6 + 5, kMod = 998244353;

int n, m; bool fl;
int col[kMaxN];
std::vector<std::vector<int>> a, b;
std::string s[kMaxN];
std::vector<std::pair<int, int>> G[kMaxN];

void dfs(int u) {
  for (auto [v, w] : G[u]) {
    if (!~col[v]) {
      col[v] = col[u] ^ w, dfs(v);
    } else if (col[v] != (col[u] ^ w)) {
      fl = 0;
    }
  }
}

void dickdreamer() {
  std::cin >> n >> m;
  a.resize(n + 2), b.resize(n + 2);
  for (int i = 1; i <= n + m; ++i) G[i].clear();
  for (int i = 1; i <= n; ++i) {
    std::cin >> s[i];
    s[i] = " " + s[i];
  }
  for (int i = 1; i <= n + 1; ++i)
    a[i].resize(m + 2), b[i].resize(m + 2);
  for (int i = 1; i <= n; ++i) {
    for (int j = 1; j <= m + 1; ++j) {
      if (j == 1) a[i][j] = 0;
      else a[i][j] = a[i][j - 1] ^ (s[i][j - 1] == 'A');
    }
    if (a[i][m + 1]) return void(std::cout << "0\n");
  }
  for (int j = 1; j <= m; ++j) {
    for (int i = 1; i <= n + 1; ++i) {
      if (i == 1) b[i][j] = 0;
      else b[i][j] = b[i - 1][j] ^ (s[i - 1][j] == 'A');
    }
    if (b[n + 1][j]) return void(std::cout << "0\n");
  }
  for (int i = 1; i <= n; ++i) {
    for (int j = 1; j <= m; ++j) {
      if (s[i][j] == 'B') {
        int v = 1 ^ a[i][j] ^ b[i][j];
        G[i].emplace_back(j + n, v), G[j + n].emplace_back(i, v);
      }
    }
  }
  std::fill_n(col + 1, n + m, -1);
  int ans = 1;
  fl = 1;
  for (int i = 1; i <= n + m; ++i) {
    if (!~col[i]) {
      col[i] = 0, dfs(i);
      if (!fl) return void(std::cout << "0\n");
      ans = 2ll * ans % kMod;
    }
  }
  std::cout << ans << '\n';
}

int32_t main() {
#ifdef ORZXKR
  freopen("in.txt", "r", stdin);
  freopen("out.txt", "w", stdout);
#endif
  std::ios::sync_with_stdio(0), std::cin.tie(0), std::cout.tie(0);
  int T = 1;
  std::cin >> T;
  while (T--) dickdreamer();
  // std::cerr << 1.0 * clock() / CLOCKS_PER_SEC << "s\n";
  return 0;
}