P7417 [USACO21FEB] Minimizing Edges P 题解

Description

Bessie 有一个连通无向图 \(G\)。\(G\) 有 \(N\) 个编号为 \(1\ldots N\) 的结点，以及 \(M\) 条边（\(2\le N\le 10^5, N-1\le M\le \frac{N^2+N}{2}\)）。\(G\) 有可能包含自环（一个结点连到自身的边），但不包含重边（连接同一对结点的多条边）。

令 \(f_G(a,b)\) 为一个布尔函数，对于每一个 \(1\le a\le N\) 和 \(0\le b\)，如果存在一条从结点 \(1\) 到结点 \(a\) 的路径恰好经过了 \(b\) 条边，则函数值为真，否则为假。如果一条边被经过了多次，则这条边会被计算相应的次数。

Elsie 想要复制 Bessie。具体地说，她想要构造一个无向图 \(G'\)，使得对于所有的 \(a\) 和 \(b\)，均有 \(f_{G'}(a,b)=f_G(a,b)\)。

Elsie 想要进行最少数量的工作，所以她想要构造最小可能的图。所以，你的工作是计算 \(G'\) 的边数的最小可能值。

\(\sum N\leq 10^5,\sum M\leq 2\times 10^5\)。

Solution

首先对于每个人一定存在 \((x_i,y_i)\)，满足 \(f_{i,j}=1\) 的条件为 \(j\) 为奇数且 \(j\geq x_i\) 或者 \(j\) 为偶数且 \(j\geq y_i\)。

那么现在可以先对于原图 \(G\) 跑 bfs 求出到每个点的奇偶最短路，得到 \((x_i,y_i)\)。注意到这里的贡献是 \(x_i+1\to y_j\) 和 \(y_i+1\to x_j\)，不太美观，考虑将其变为 \((a_i,b_i)\) 表示到 \(i\) 的最短路和与最短路奇偶性不同的最短路。

则一定满足 \(a_i<b_i\) 且 \(a_i\) 和 \(b_i\) 奇偶性不同。

此时对于 \(i\)，要贡献出 \((a_i,b_i)\)，就一定要满足 \(i\) 的邻域存在一个 \(a_j=a_i-1\)，且存在 \(a_k=b_i-1\) 或者 \(b_k=b_i-1\)。同时还需要满足所有与 \(i\) 相邻的 \(j\) 都有 \(|a_i-a_j|\leq 1\)。所以 \((a_i,b_i)\) 只会连如下边：

1. \((a_i-1,b_i-1)\)
2. \((a_i-1,b_i+1),(a_i+1,b_i-1)\)

可以证明这两种连边满足条件，且不存在其余更优的连法。

现在如果把 \((a_i,b_i)\) 放到二维平面上，第一种相当于往左上方连边，第二种是同时往右上、左下连边。特别的，当 \(a_i+1=b_i\) 时第二种是往自己和左下连边。

注意到上面的连法可以按照 \(a_i+b_i\) 分层，如下图：

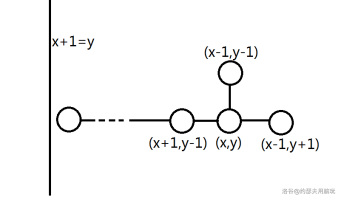
考虑对于同层内的点从左往右进行贪心，设 \(i\) 有 \(t\) 个点，\(cnt\) 表示 \(i-1\) 往 \(i\) 要连 \(cnt\) 条边。

1. 如果 \(i\) 上方没有点，就只能连层内边，所以 \(ans\leftarrow ans+\max\{t,cnt\},cnt\leftarrow t\)。

2. 如果 \(i\) 上方有点，还要分两种情况讨论：

• 如果 \(t\geq cnt\)，则 \(t\) 中要分 \(cnt\) 个点连左边，剩余的全连上面。
• 如果 \(t<cnt\)，则 \(t\) 个点全要连左边。

枚举到最后，如果在 \((x,x+1)\) 剩余 \(cnt\) 个点要连右边，则一定是它们内部两两连边，即 \(ans\leftarrow\left\lceil\frac{cnt}{2}\right\rceil\)。

具体见代码。

时间复杂度：\(O(N\log N)\)。

Code