CF506E Mr. Kitayuta's Gift 题解

Description

给定一个长度为 \(n\) 的小写字符串 \(s\) 和一个正整数 \(m\)。

要求在 \(s\) 中插入恰好 \(m\) 个小写字符使其回文的方案数，两个方案不同当且仅当它们得到的串不同，与插入顺序和位置无关。

\(n \le 200,m \le 10^9\)，答案对 \(10^4 + 7\) 取模。

Solution

先考虑 \(n+m\) 为偶数的情况。

设 \(f_{i,l,r}\) 表示最终的字符串的前 \(i\) 与后 \(i\) 位与 \(s\) 尽量匹配，最终剩下 \(s_{l,\dots,r}\) 没有匹配的方案数，\(g_i\) 表示前 \(i\) 位与后 \(i\) 位已经能与 \(s\) 完全匹配的方案数。

容易发现答案是 \(g_{(n+m)/2}\)。考虑转移。

如果 \(s_l=s_r\) 且 \(r-l\leq 1\)，则 \(g_{i+1}\leftarrow f_{i,l,r},f_{i+1,l,r}\leftarrow 25\cdot f_{i,l,r}\)。

如果 \(s_l=s_r\) 且 \(r-l>1\)，则 \(f_{i+1,l+1,r-1}\leftarrow f_{i,l,r},f_{i+1,l,r}\leftarrow 25\cdot f_{i,l,r}\)。

如果 \(s_l\neq s_r\)，则 \(f_{i+1,l+1,r}\leftarrow f_{i,l,r},f_{i+1,l,r-1}\leftarrow f_{i,l,r},f_{i+1,l,r}\leftarrow 24\cdot f_{i,l,r}\)。

并且 \(g_{i+1}\leftarrow 26\cdot g_i\)。

可以发现这个东西的转移图是个自动机。一个点 \(s_{l,r}\) 如果满足 \(s_l=s_r\) 则有 \(25\) 个自环，否则有 \(24\) 个自环，起点为 \(s_{l,r}\)，终点有 \(26\) 个自环。不妨设 \(24\) 个自环的为红点，\(25\) 个的为绿点，可以发现图长这样：

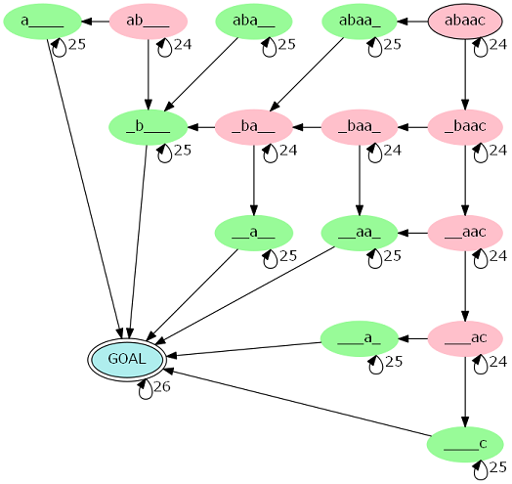
于是题目转化为在求在这个图上有多少个长度为 \(n+m\) 的从起点到终点的路径，可以用矩阵乘法做到 \(O\left(n^6\log (n+m)\right)\)，显然过不了。

---

考虑优化。

注意到对于图中的一个从起点到终点的不包含自环的链，\(2cnt_{25}+cnt_{24}=n或n+1\)，所以 \(cnt_{25}=\left\lceil\frac{n-cnt_{24}}{2}\right\rceil\)，那么图中只有 \(O(n)\) 种不同的链，如下图：

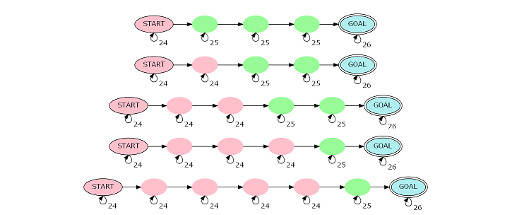
所以可以对于每种链，求出这种链的出现次数再乘上这个链的方案数即可。

可以做到 \(O\left(n^4\log (n+m)\right)\)。

---

但是还是过不了。

注意到上面那个做法有很多浪费，因为这 \(n\) 条链有很多结构是类似的，可以把他们压到一张图上：

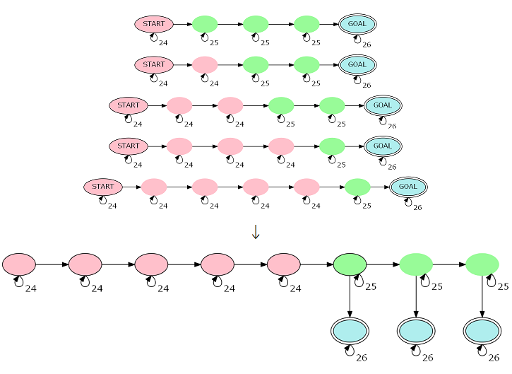
那么先跑一遍矩乘就可以 \(O(1)\) 求出任意两点间的方案数，于是做到 \(O\left(n^3\log (n+m)\right)\) 了。

还有 \(n+m\) 为奇数的情况。

这里先求出长度为 \(n+m+1\) 的答案，可以发现多算的部分就是最后一步从形如 \(s_{l,l+1}\) 的绿点走到终点的方案数，所以可以跑出 \(n+m-1\) 的矩阵，再枚举这样的 \(s_{l,l+1}\) 和对应的起点减去答案即可。

时间复杂度：\(O\left(n^3\log (n+m)\right)\)。

Code

#include <bits/stdc++.h>

// #define int int64_t

const int kMaxN = 205, kMaxM = 405, kMod = 1e4 + 7;

int n, m, len;
int f[kMaxN][kMaxN][kMaxN];
std::string s;

inline int add(int x, int y) { return (x + y >= kMod ? x + y - kMod : x + y); }
inline int sub(int x, int y) { return (x >= y ? x - y : x - y + kMod); }
inline void inc(int &x, int y) { (x += y) >= kMod ? x -= kMod : x; }
inline void dec(int &x, int y) { (x -= y) < 0 ? x += kMod : x; }

struct Matrix {
  int n, m, a[kMaxM][kMaxM];

  void set(int _n, int _m) { n = _n, m = _m; }
  friend Matrix operator*(const Matrix &m1, const Matrix &m2) {
    static Matrix ret;
    assert(m1.m == m2.n);
    ret.set(m1.n, m2.m);
    for (int i = 1; i <= m1.n; ++i) {
      for (int j = i; j <= m2.m; ++j) {
        ret.a[i][j] = 0;
        for (int k = i; k <= j; ++k)
          inc(ret.a[i][j], 1ll * m1.a[i][k] * m2.a[k][j] % kMod);
      }
    }
    return ret;
  }
} M, S, O;

void prework() {
  len = n + m;
  for (int i = 0; i <= n + 1; ++i)
    for (int j = 0; j < i; ++j) f[i][j][0] = 1;
  for (int len = 1; len <= n; ++len) {
    for (int i = 1; i <= n - len + 1; ++i) {
      int j = i + len - 1;
      for (int k = 0; k <= n; ++k) {
        if (s[i] == s[j])
          inc(f[i][j][k], f[i + 1][j - 1][k]);
        else
          inc(f[i][j][k + 1], add(f[i][j - 1][k], f[i + 1][j][k]));
      }
    }
  }
}

int calc(int l, int r, int k) {
  static int f[kMaxN][kMaxN][kMaxN] = {0};
  static bool vis[kMaxN][kMaxN][kMaxN] = {0};
  if (l >= r || k < 0) return 0;
  else if (l + 1 == r && s[l] == s[r]) return !k;
  else if (vis[l][r][k]) return f[l][r][k];
  vis[l][r][k] = 1;
  if (s[l] == s[r]) f[l][r][k] = calc(l + 1, r - 1, k);
  else f[l][r][k] = add(calc(l, r - 1, k - 1), calc(l + 1, r, k - 1));
  return f[l][r][k];
}

Matrix qpow(Matrix bs, int idx) {
  Matrix ret = bs;
  --idx;
  for (; idx; idx >>= 1, bs = bs * bs)
    if (idx & 1) ret = ret * bs;
  return ret;
}

void dickdreamer() {
  std::cin >> s >> m;
  n = s.size(), s = " " + s;
  prework();
  for (int i = 0; i <= n; ++i) std::cerr << f[1][n][i] << ' ';
  int cnt24 = n - 1, cnt25 = (n + 1) / 2, sz = cnt24 + 2 * cnt25;
  M.set(sz, sz), S.set(1, sz);
  for (int i = 1; i <= cnt24; ++i) M.a[i][i] = 24;
  for (int i = cnt24 + 1; i <= cnt24 + cnt25; ++i) M.a[i][i] = 25;
  for (int i = cnt24 + cnt25 + 1; i <= sz; ++i) M.a[i][i] = 26;
  for (int i = 1; i < cnt24 + cnt25; ++i) M.a[i][i + 1] = 1;
  for (int i = cnt24 + 1; i <= cnt24 + cnt25; ++i) M.a[i][i + cnt25] = 1;
  auto tmp = qpow(M, len / 2);
  int ans = 0;
  if (len & 1) {
    for (int i = 0; i <= cnt24; ++i) {
      dec(ans, 1ll * calc(1, n, i) * tmp.a[cnt24 - i + 1][cnt24 + (n - i) / 2] % kMod);
    }
    tmp = tmp * M;
  }
  for (int i = 0; i <= cnt24; ++i) {
    inc(ans, 1ll * f[1][n][i] * tmp.a[cnt24 - i + 1][cnt24 + cnt25 + (n - i + 1) / 2] % kMod);
  }
  std::cout << ans << '\n';
}

int32_t main() {
#ifdef ORZXKR
  freopen("in.txt", "r", stdin);
  freopen("out.txt", "w", stdout);
#endif
  std::ios::sync_with_stdio(0), std::cin.tie(0), std::cout.tie(0);
  int T = 1;
  // std::cin >> T;
  while (T--) dickdreamer();
  // std::cerr << 1.0 * clock() / CLOCKS_PER_SEC << "s\n";
  return 0;
}