Word Window 分类与神经网络
符号表示
- x表示单词或者词向量。y表示词序列。

分类
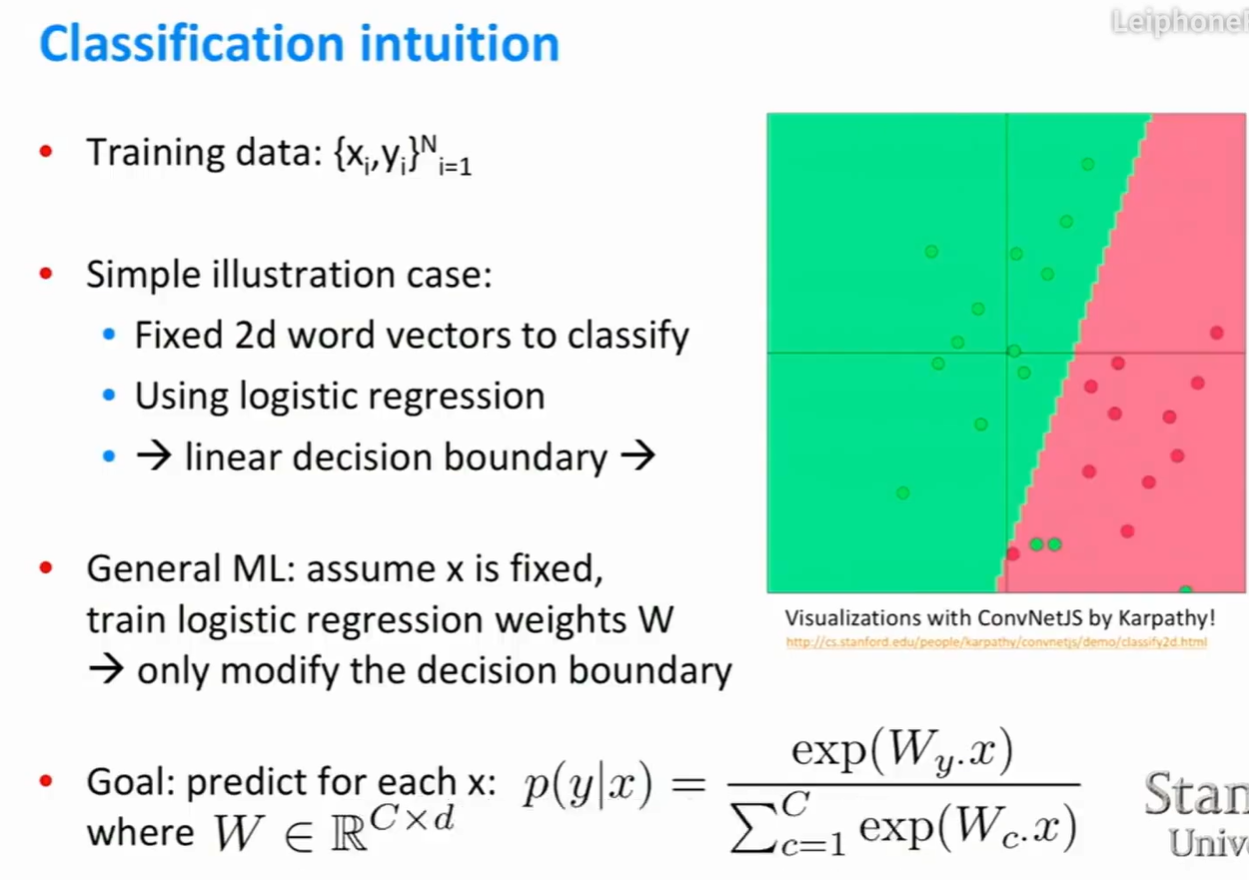
- 通常情况下,假设输入x是给定的,训练逻辑回归的权重w(只修改决策边界)。
Softmax
将计算分为两步:
- 第一步,用W的第y行乘以向量x,得到向量$f_y$。
- 然后将向量$f_y$输入到Softmax,得到一个概率分布。


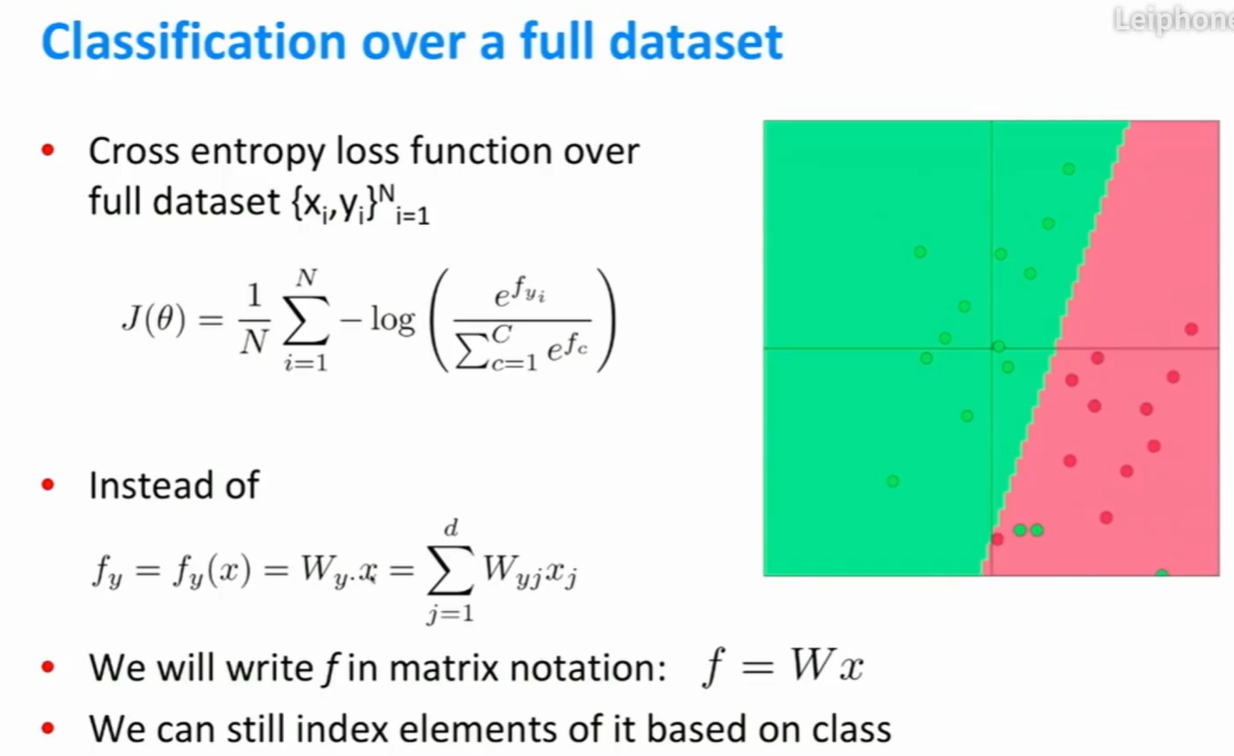
交叉熵误差
- 举例:假设有五个类别,正确的类别是第三个类别(标记为1)。理想的概率为p(c),通过softmax计算得到的概率为q(c)。
- 在这个例子中,p(c)是一个独热编码向量,所以非正确类别的求和项的值全部为0.
- 最后交叉熵的结果是log(q),即softmax的计算结果。

- $y_i$表示正确的类别,目标是最小化整个求和项,即最小化交叉熵。
正则项
- 逻辑回归中,加入正则项主要是为了令所有权值尽可能的小(接近0)。
- 当有大量特征的时候,加入正则项可以尽可能地避免过拟合的情况。
- x轴表示训练迭代次数或者其它。

传统机器学习中的优化

深度学习中的词向量
- 词向量多,可能会出现过拟合的情况。

单词分类
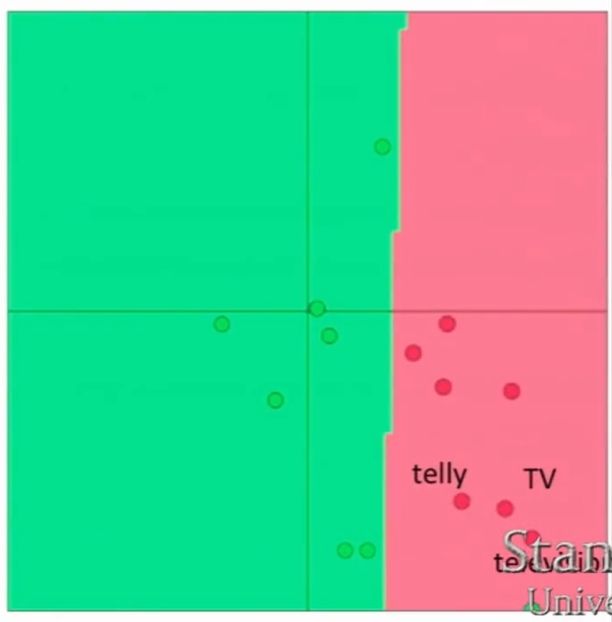
- 举例:将单词分类为消极或积极。训练集中包含TV和telly两个单词。测试集中有television这个单词。
- 通过Word2vec或Glove算法进行训练,发现三个单词出现在相似的上下文中,所以它们在向量空间的位置非常接近。
- 当我们对单词进行情感色彩分类时,结果发生了变化。但television依然在它原来的位置。
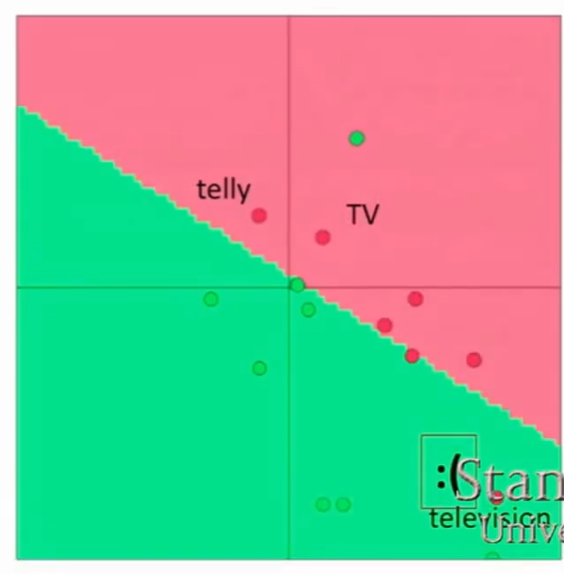
进行情感色彩分类后的结果
- 结果表明,使用深度学习在一个小型数据集上训练,可能会出现过拟合的结果,模型的泛化能力下降。所以在一个小型数据集上,除了将词向量初始化外,不需要做其他的操作。
Window classification
- 举例:将大语料库中的每个单词进行四分类:人名,地点,组织以及其它。
- 首先要将中心词进行分类,然后将以它为中心词的窗口作为一个词向量(词向量通常为一个列向量)。
- 下图将Paris作为中心词,定义窗口长度为2(中心词左右各有2个单词)。x是一个d维向量,由5个单词组成。

窗口分类器
- $\hat{y}$表示当前的正确类别。

更新词向量
- 方法:求导。
- 第一步:对符号进行定义并记住它们的维度。
- 第二步:使用链式法则。
- 第三步:注意$f_c$中的c有两种情况,c等于 正确类别 以及c等于 所有非正确类别。
- 第四步:正确类别的$\hat{y}$需要减去1。
- 第五步:为了更好地实现,将“减去1”这个步骤改为[$\hat{y}$-t]。同时将$\hat{y}$-t定义为δ。




窗口向量梯度的维度


矩阵实现

代码
from numpy import random N = 500 # 需要分类的窗口总数 d = 300 # 每个窗口的维度 C = 5 # 类别总数,一共有五个类别 W = random.rand(C,d) wordvectors_list = [random.rand(d,1) for i in range(N)] # 每个词向量 wordvectors_one_matrix = random.rand(d,N) # 也可以将词向量全部放在一个矩阵里面 %timeit [W.dot(wordvectors_list[i]) for i in range(N)] %timeit W.dot(wordvectors_one_matrix)
神经网络
对单个神经元的定义
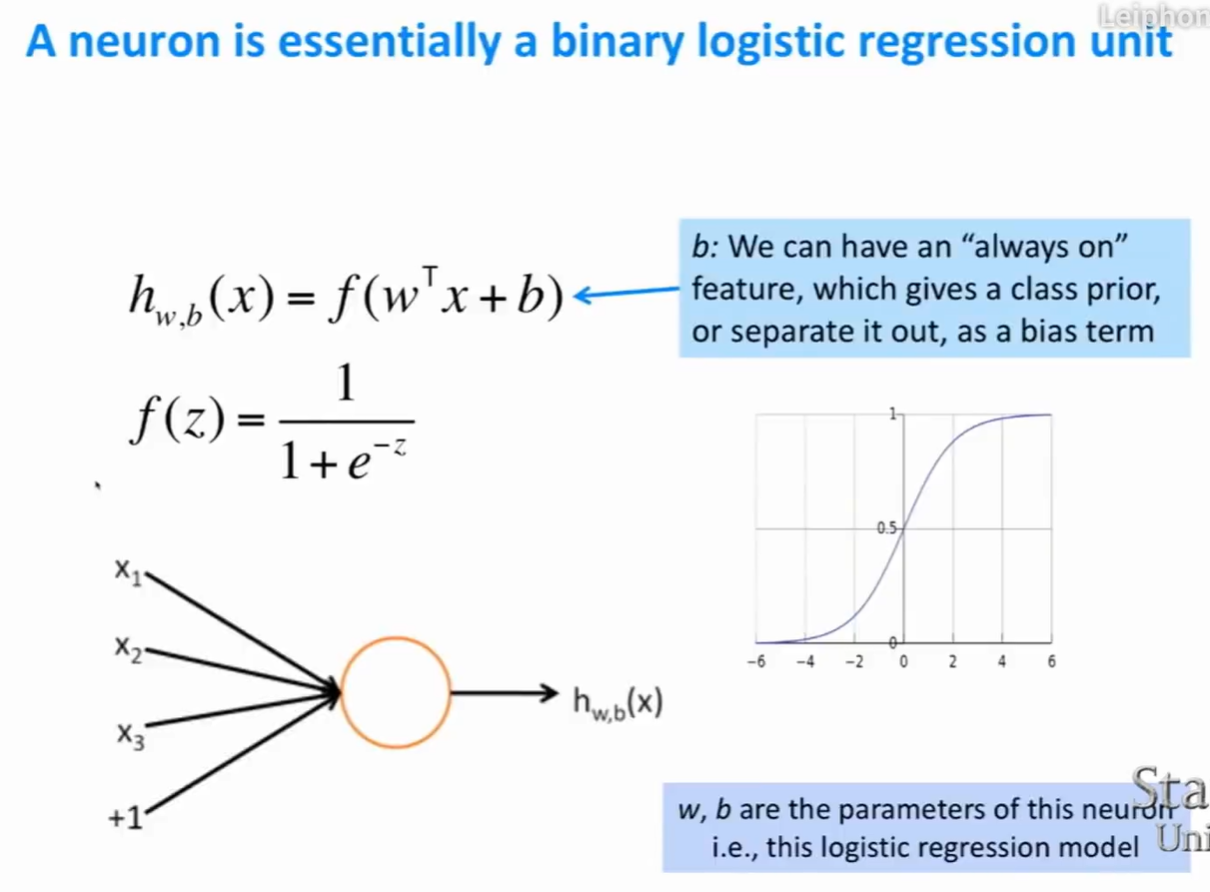
矩阵表示形式
- 偏置项b的维度与这一层的神经元数量相等。
- W的行数是神经元的数量。W的列数是输入x的维度。

前向传播

损失函数 (Max-margin Objective)
- 目标是为了让正确窗口的得分比较高,非正确窗口的得分较低。
- s是正样本的得分,$s_c$是负样本的得分。

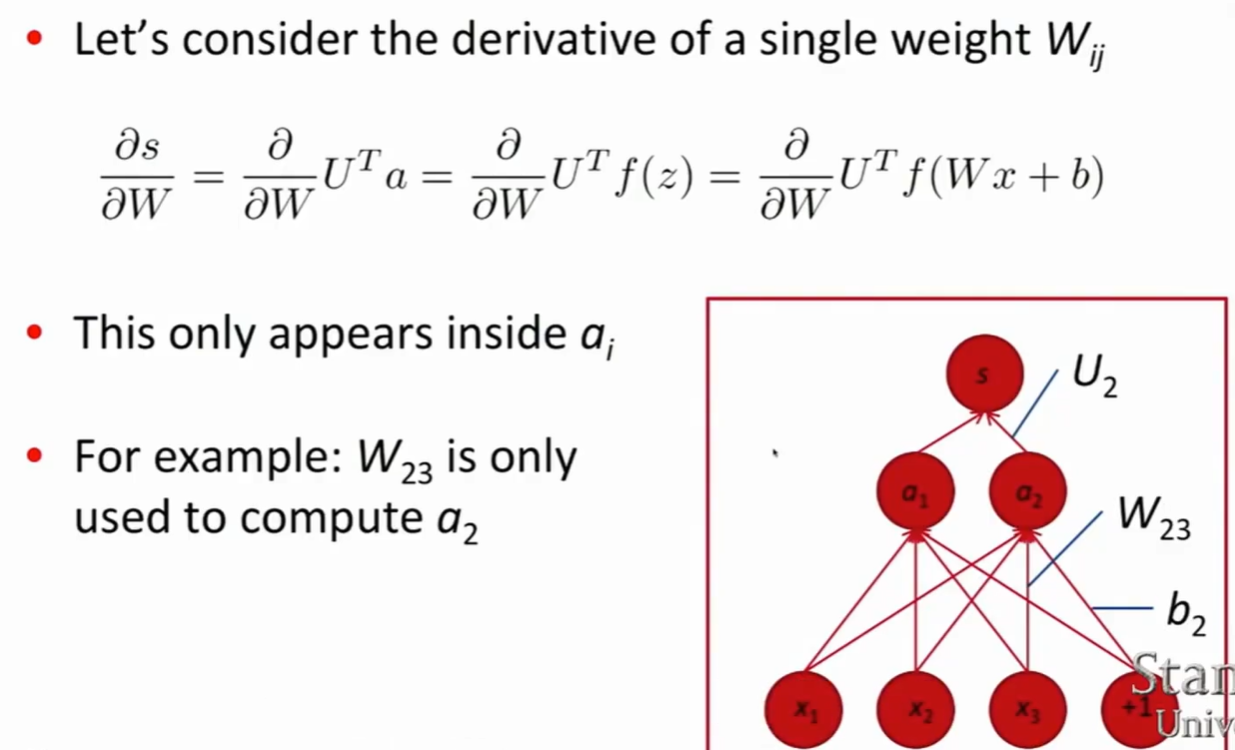
优化

- 对$W_{ij}$求导,只需要考虑$\vec{a}$的第i个元素。
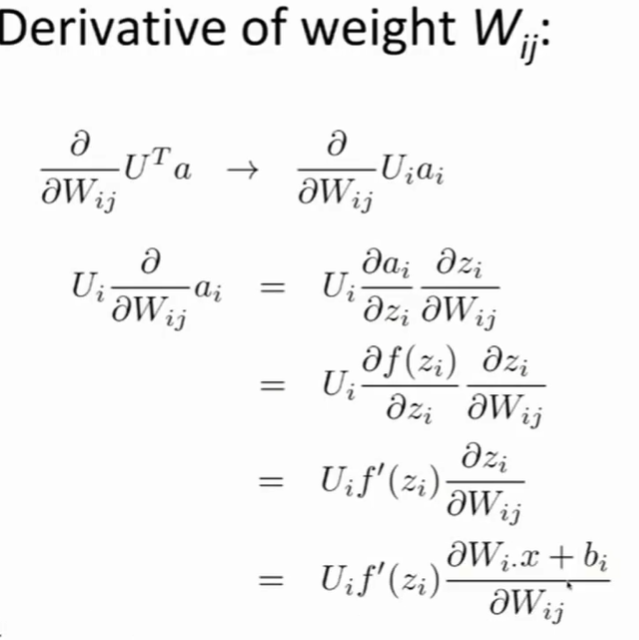
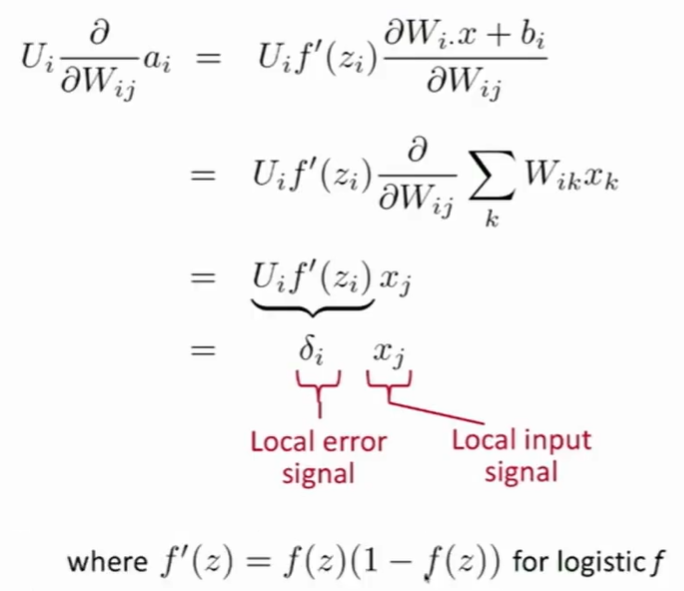
- 对$b_i$求导,
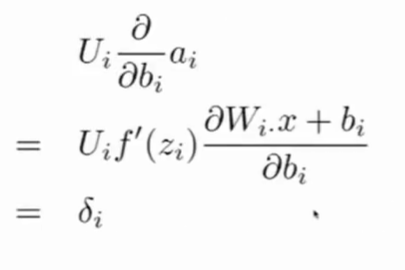
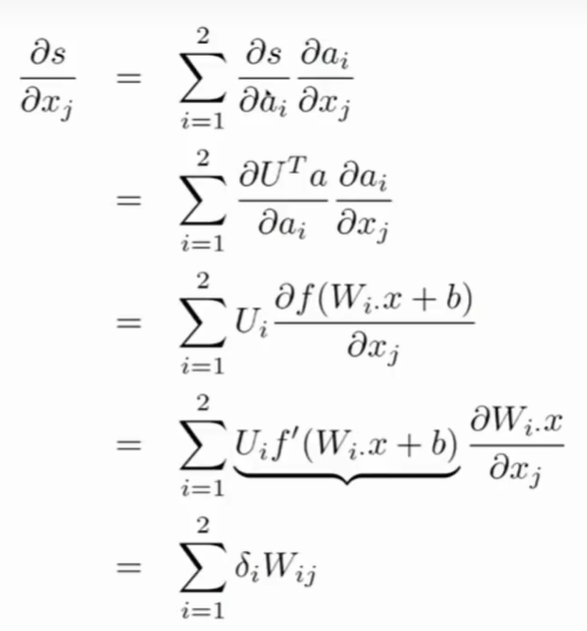
- {1-s+$s_c$>0}为真,则等于1,否则为0.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号