共现矩阵 Glove算法 词向量评估

如何运用word2vec进行高效训练

• 将常见的单词组合（word pairs）或者词组作为单个“words”来处理。

• 对高频出现的单词进行抽样，减少训练样本的个数。

• 对优化目标采用负采样(negative sampling)，即每次让一个训练样本仅仅更新一小部分的权重，从而降低计算负担。

详细内容参考：理解 Word2Vec 之 Skip-Gram 模型 - 知乎 (zhihu.com)。

 

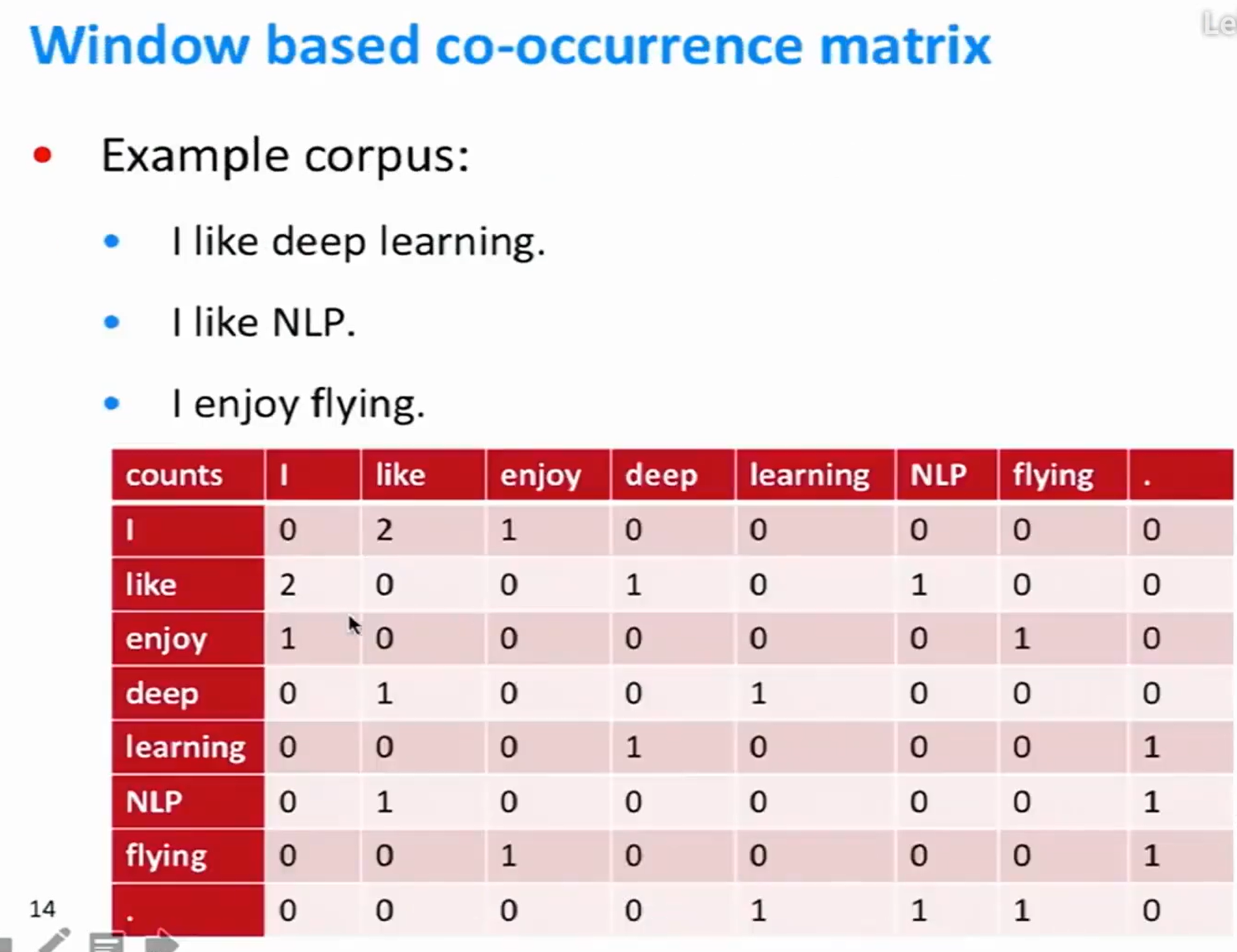
基于窗口的共现矩阵

• 无论左右的单词是否有关，矩阵是对称的。

 

共现向量的缺点

• 如果词典中有一个新单词，词向量就会随之变化，参数可能会出现缺失。
• 维数过高，训练机器学习模型时，可能会存在稀疏性问题。

解决方法

• 将向量固定在较小的维度（密集向量）。与word2vec相似，维度通常在25-1000之间。
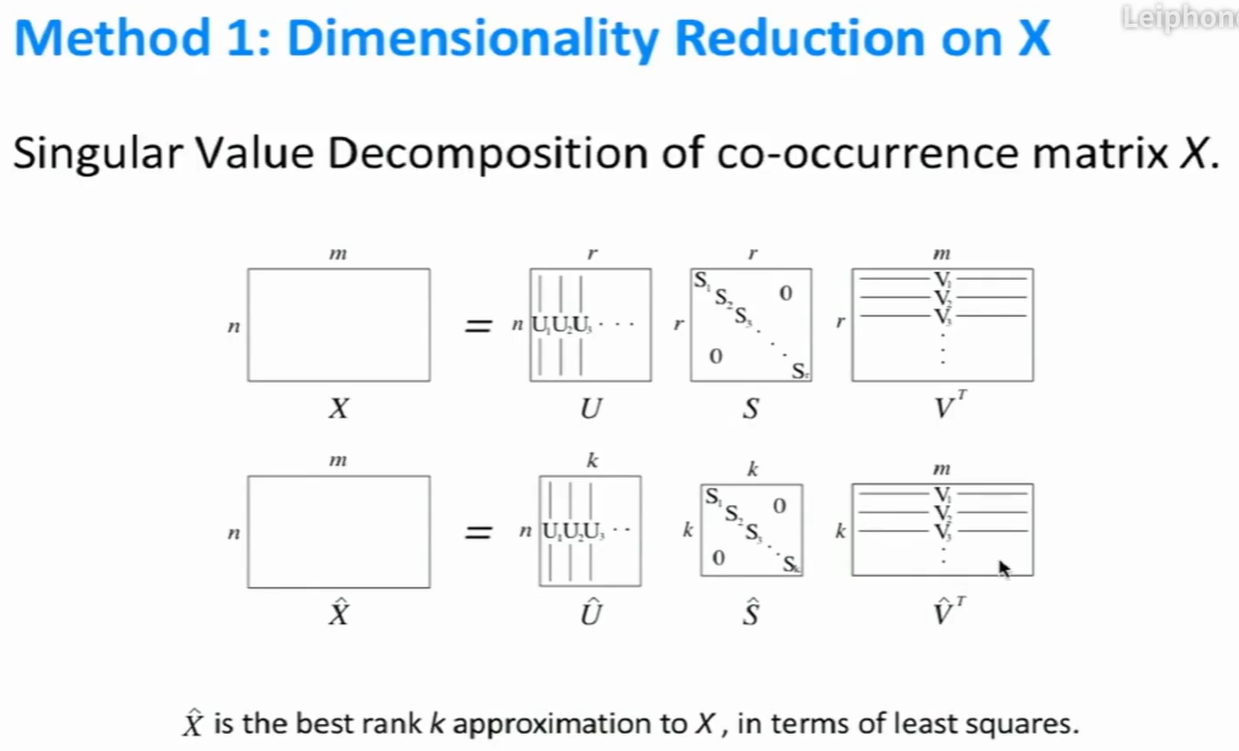
• 降维方法：奇异值分解 (SVD)。　　

 

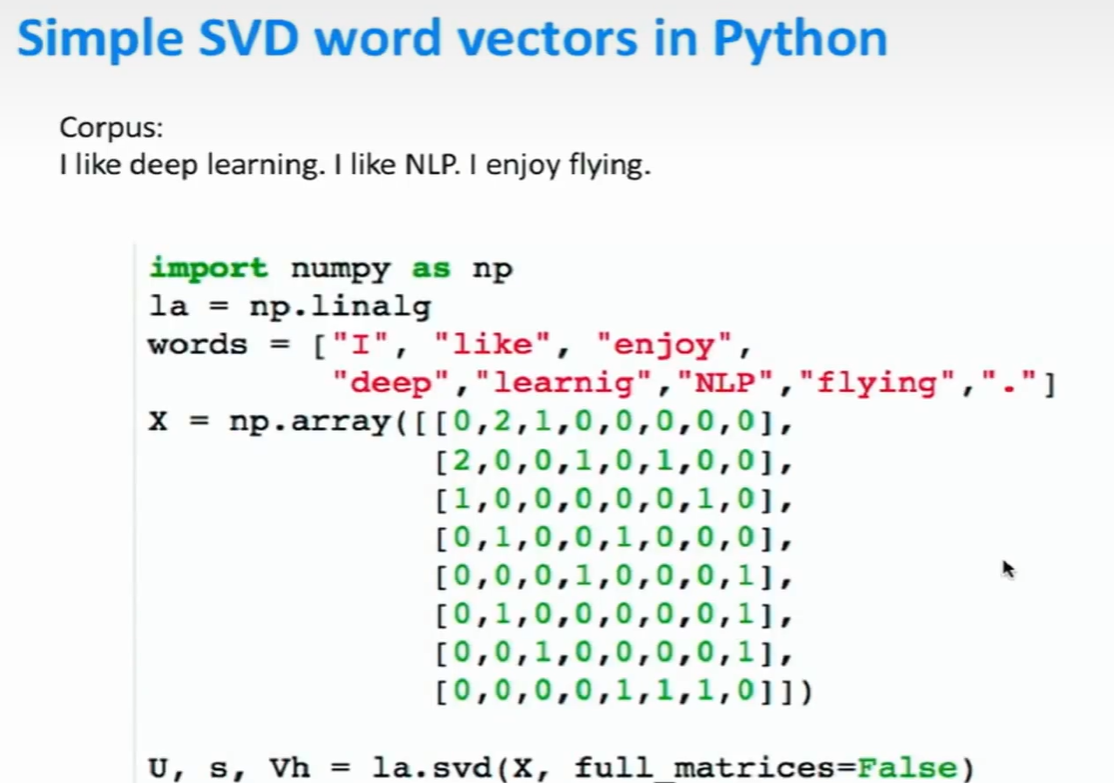
代码

import numpy as np
la = np.linalg
words = ["I","like","enjoy","deep","learning","NLP","flying","-"]
X = np.array([[0,2,1,0,0,0,0,0],
　　　　　　　　[2,0,0,1,0,1,0,0],
　　　　　　　　[1,0,0,0,0,0,1,0],
　　　　　　　　[0,1,0,0,1,0,0,0],
　　　　　　　　[0,0,0,1,0,0,0,1],
　　　　　　　　[0,1,0,0,0,0,0,1],
　　　　　　　　[0,0,1,0,0,0,0,1],
　　　　　　　　[0,0,0,0,1,1,1,0]])

U,s,Vh = la.svd(X,full_matrices=False)　　#s为对矩阵la的奇异值分解。对角线元素（奇异值）从大到小排列。

关于full_matrices

• full_matrices的取值是为0或者1，默认值为1，这时u的大小为(M,M)，v的大小为(N,N) 。否则u的大小为(M,K)，v的大小为(K,N) ，K=min(M,N)。

 

 

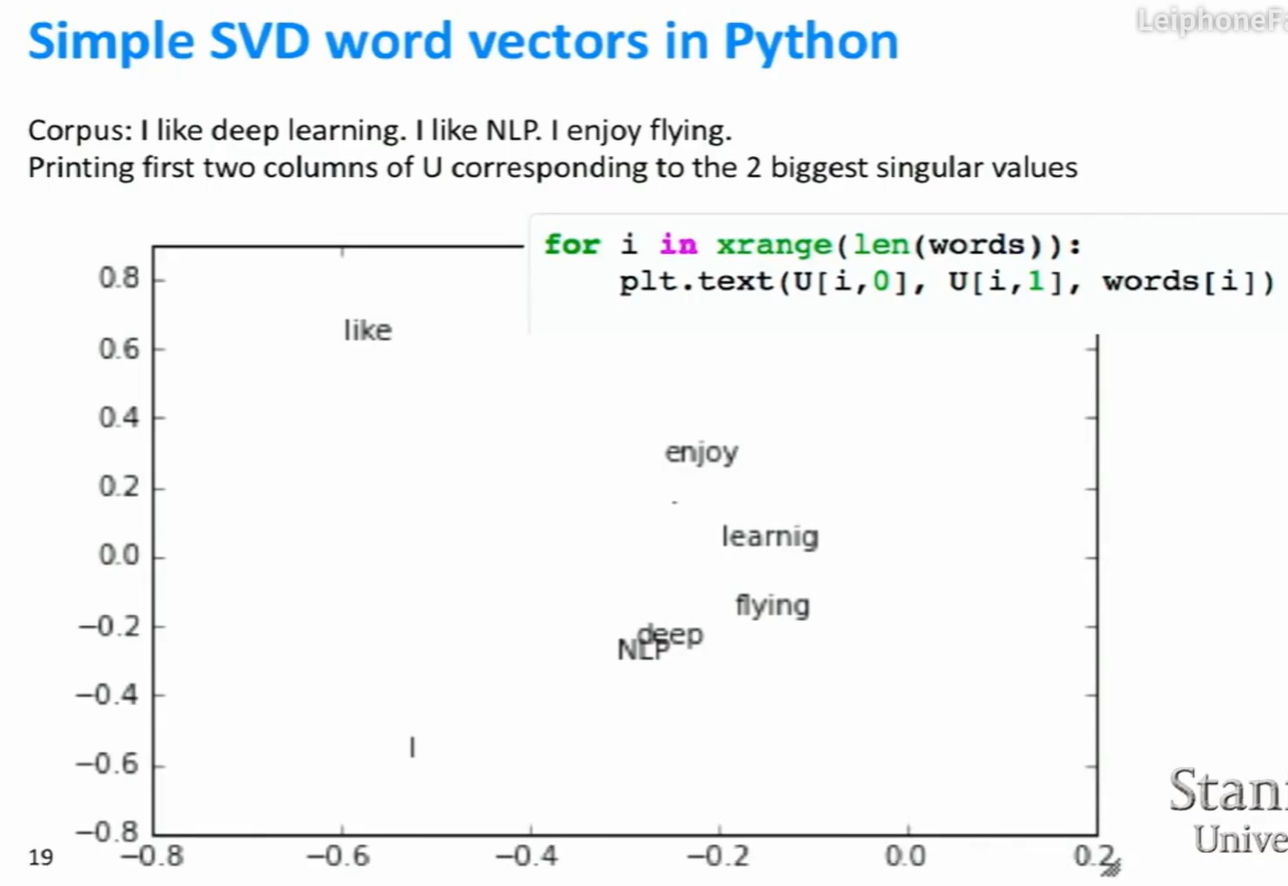
处理共现矩阵

 

GloVe算法

• P表示共现矩阵。

 

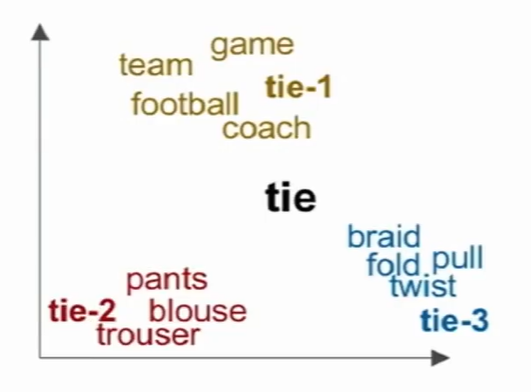
多义词的处理

• 分解为多义向量。
• 下图中的tie向量，实际上是tie-1，tie-2，tie-3这些多义向量的线性叠加。
• 可以通过稀疏编码来对多义词进行语境解释。

 

　　

稀疏编码

 

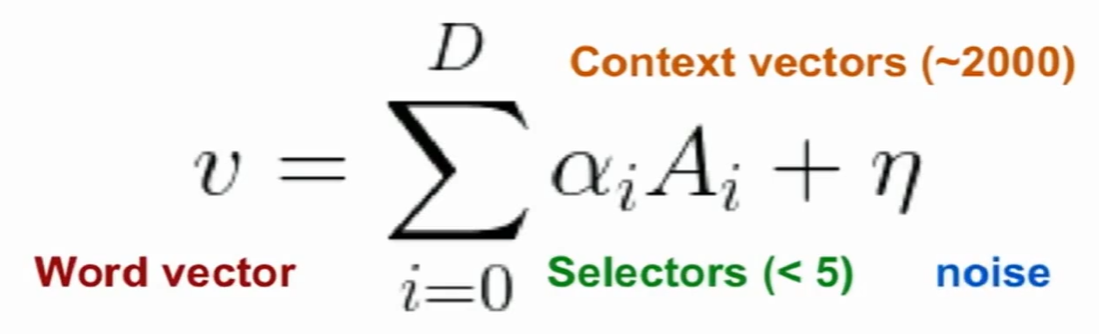
内部和外部评估词向量

词向量的内部评估

单词向量类比法

• 通过向量之间的余弦距离进行类比。
• 例如：man类比于woman，就像king类比于queen。将$x_b$，$x_a$，$x_c$代入公式，然后找到最大的余弦相似性向量$x_i$。

 

 

 

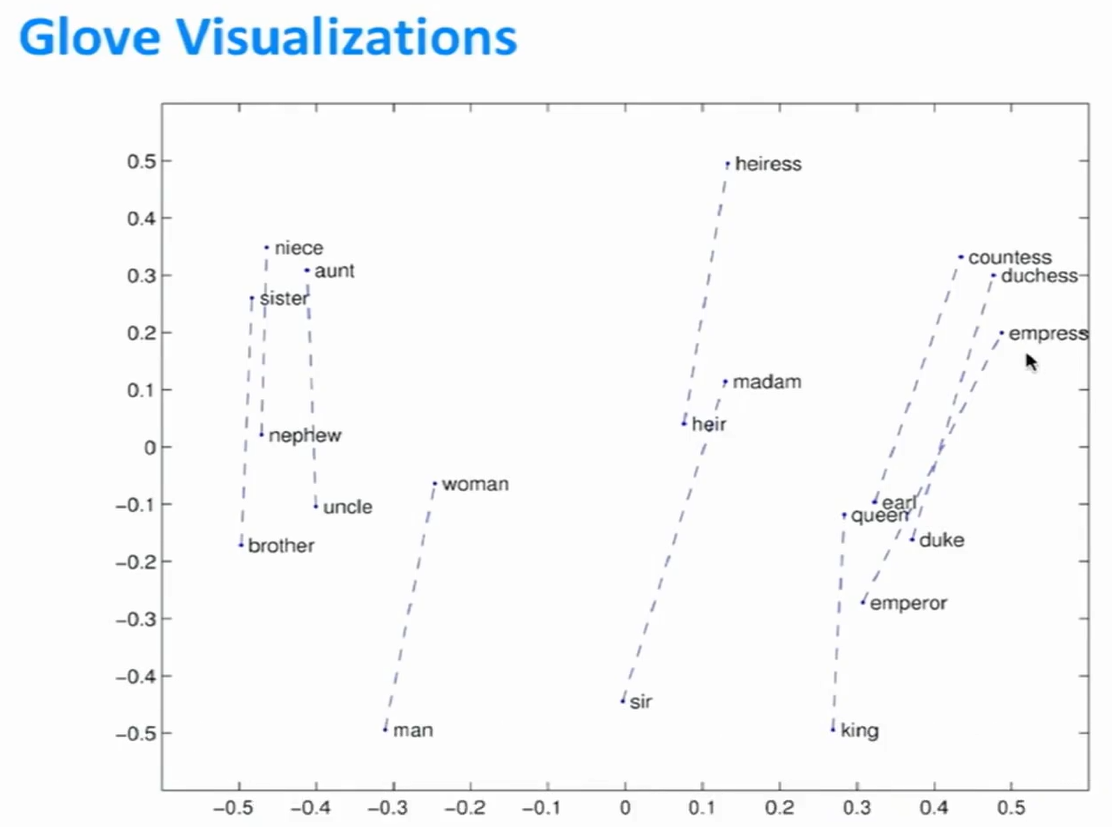
• 不仅适用于语义关系，还适用于句法关系。

 

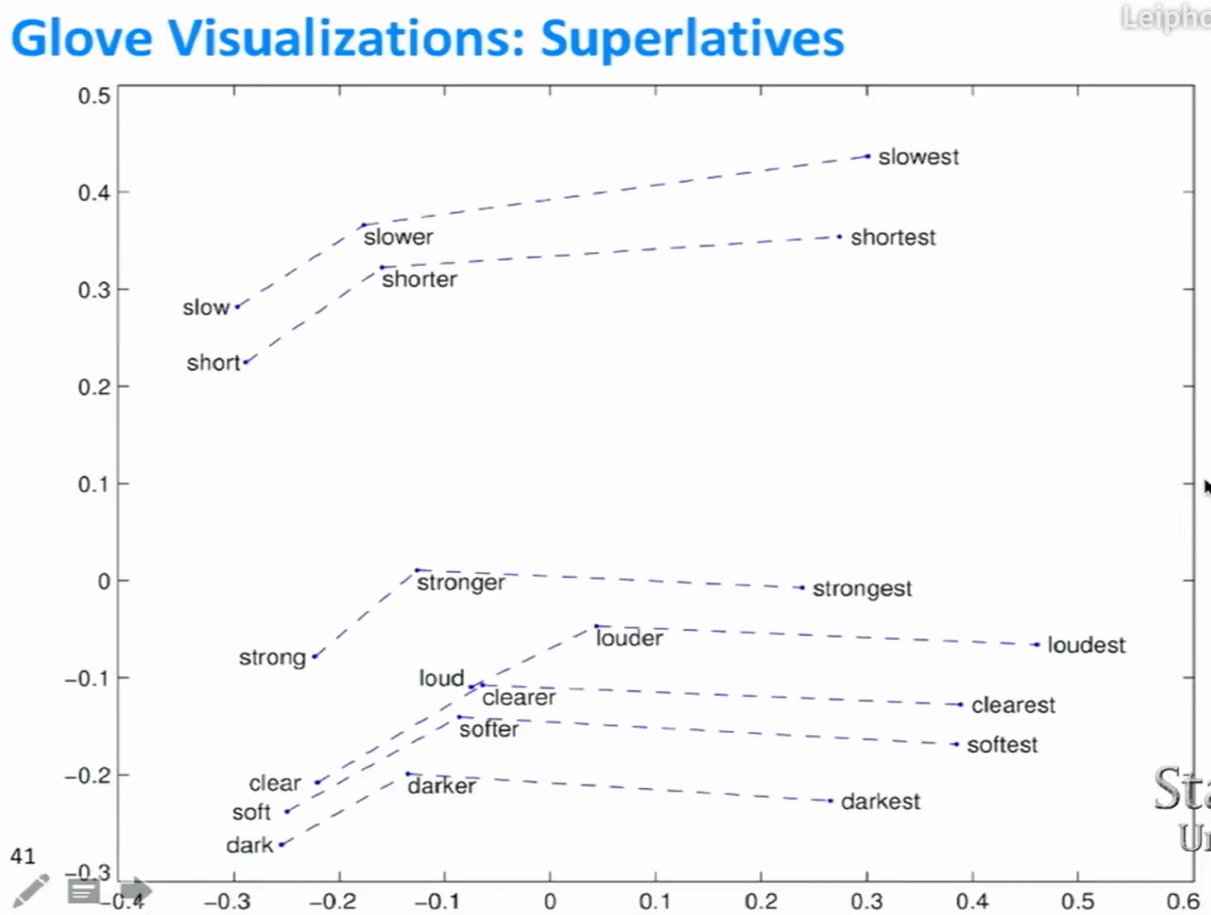
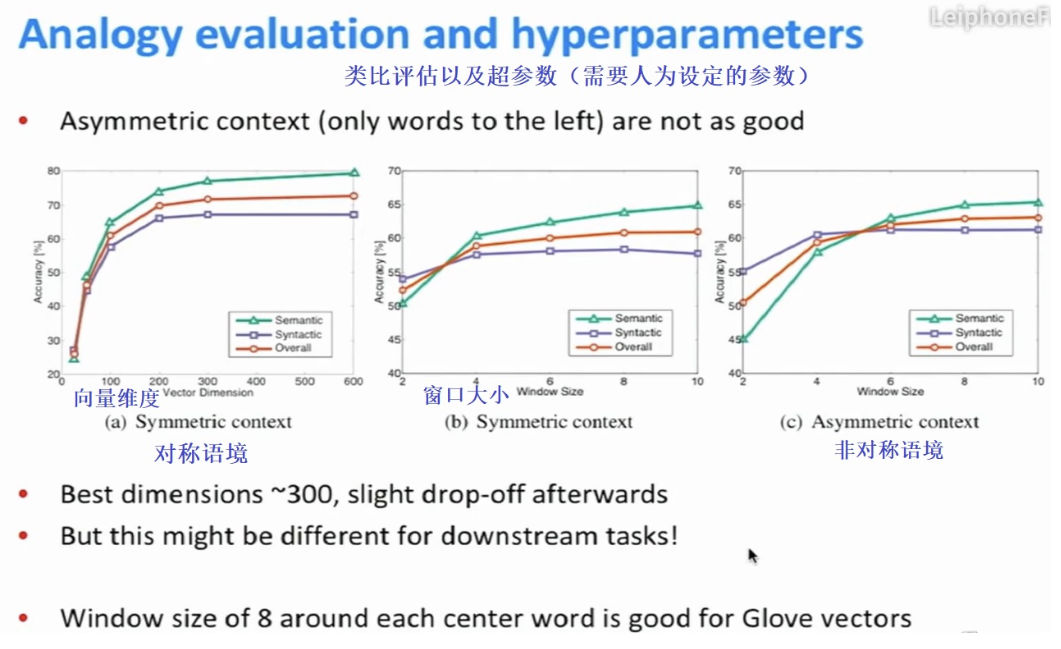
词向量维度，窗口尺寸以及窗口对称性，对于语义语法任务的影响

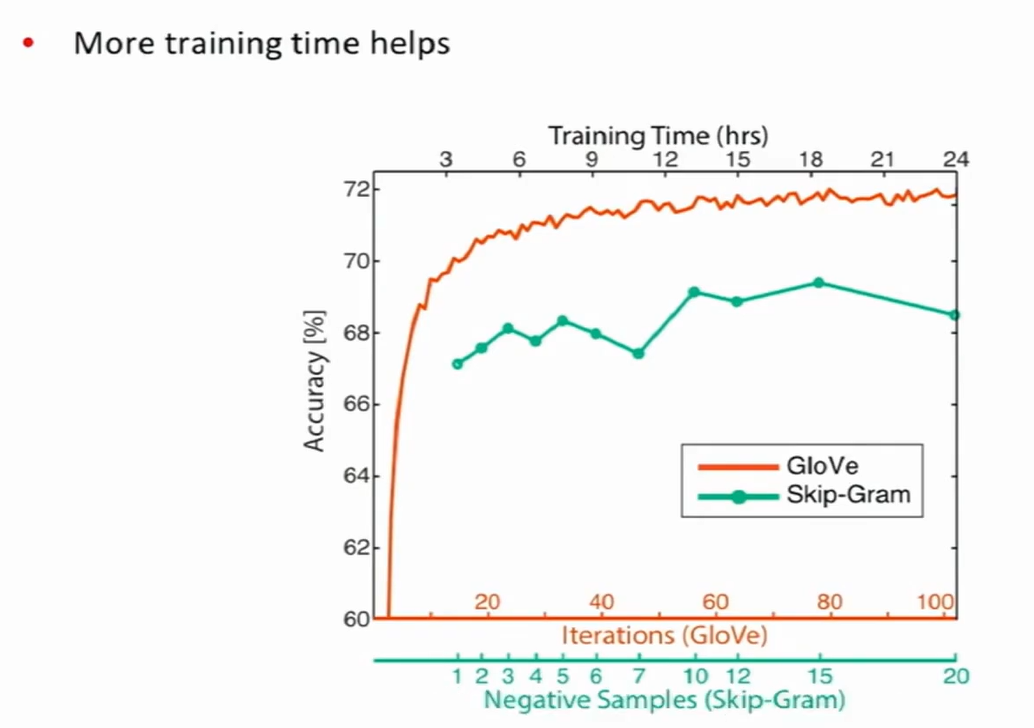
Glove和Skip-Gram之间的对比

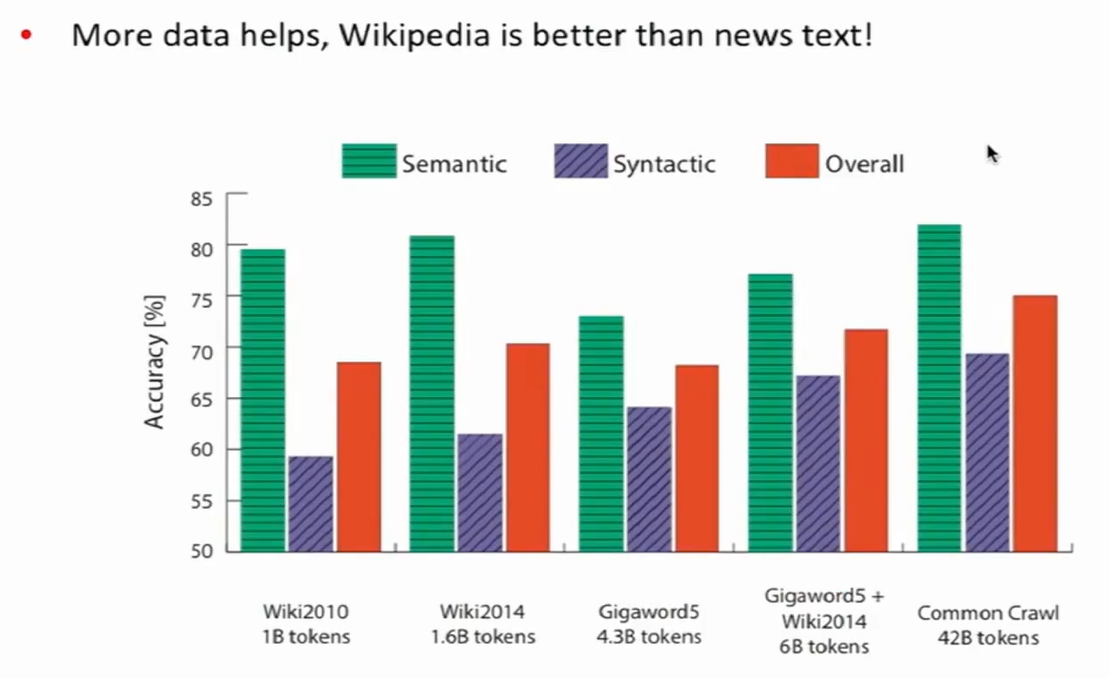
语料库大小对语法任务的影响

• 海量的数据有助于提高模型的精准性。

 

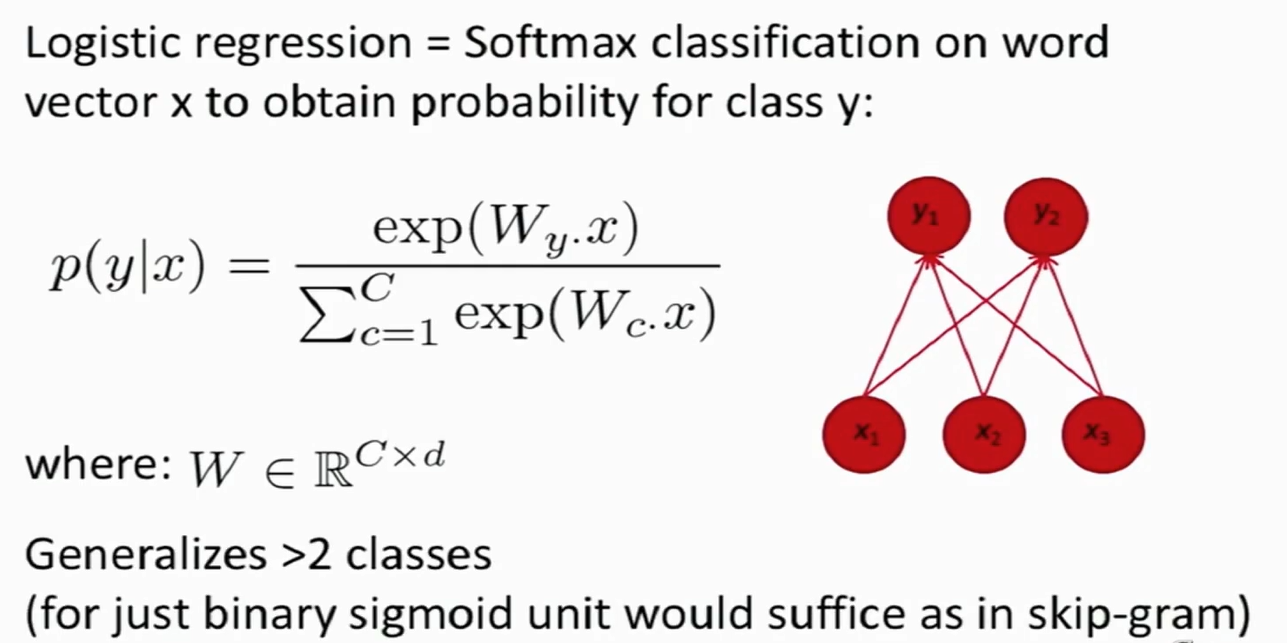
对单词进行分类：使用Softmax

• 对不同的类别构建矩阵$W_y$，y是行数，每行代表不同的类别，x是单词向量。
• W矩阵用于分类，大小为C×d，d是输入向量的维数，C是拥有的类别数。
• 例：分类的目标是判断单词是否为地区名词。