左叶子节点之和

首先将非终止条件，非递归函数部分叫做单层递归。

思考过程如下：

• 首先想总的思路：就是找到左子树的左叶子节点将它的值加到sum上，然后找到右子树的左叶子结点将它的值加到sum上，最后将它们的值相加就是左叶子结点之和，由此我们可以写出递归部分

 

leftsum(node->left, sum);
leftsum(node->right, sum);

 

• 想我在左子树中要实现什么在右子树要实现什么；要实现的内容为：一个节点的左节点的左节点为空，左节点的右节点为空，那么这个结点就是左叶子结点，那么我们就要给它的数值加到sum上去，由此可写出单层循环的部分

    if ((node->left->left == nullptr) && (node->left->right == nullptr)) {
        sum += node->left->data_;
    }

• 确定终止条件：二叉树的终止条件就是不能让当成循环中出现nullptr->left和nullptr->right，那么我们将将递归逻辑图画出：

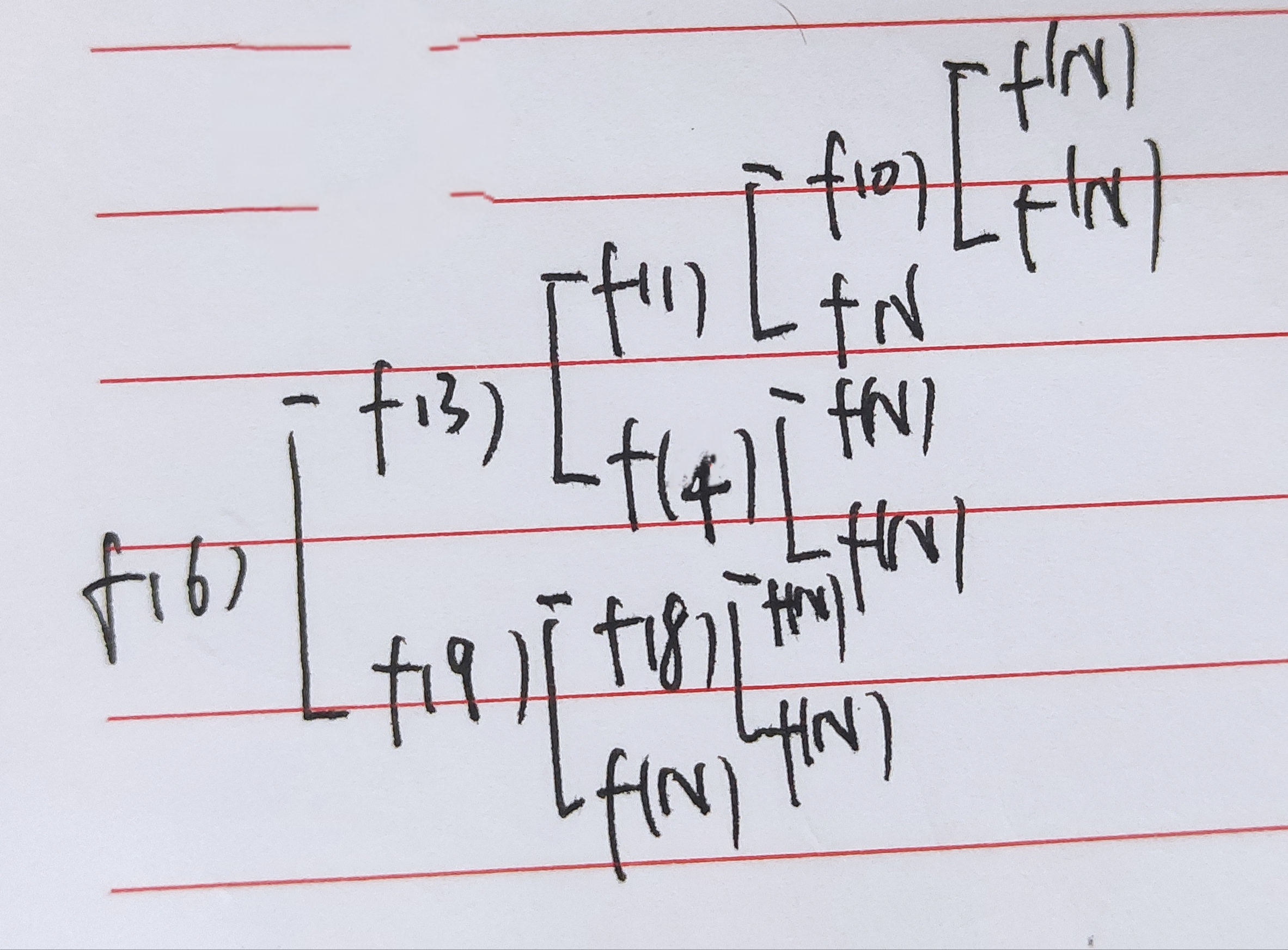
首先f(N)肯定不行单层递归里以node->left->left为例，光是node->left就已经不行了，因此node==nullptr时我们就应该return;

f(0)肯定也不行node->left为nullptr，在求nullptr的左节点肯定不合理，因此node->left或则node->right为nullptr时我们就应该return;

因此整体代码为：

//sum每次递归都要用，但是又不想重新初始化sum，那么就将它作为形参，并且把它变成引用
void leftsum(Node* node,int &sum) {
    if (node == nullptr) return;
    if ((node->left == nullptr) && (node->right == nullptr)) return;
    if ((node->left->left == nullptr) && (node->left->right == nullptr)) {
        sum += node->left->data_;
    }
    leftsum(node->left, sum);
    leftsum(node->right, sum);
}

力扣上的解题步骤：

如果按照力扣上的要求，我们必须由返回值返回左叶子之和的话，那么我们就用来解题的树就不能随便画，必须画成：

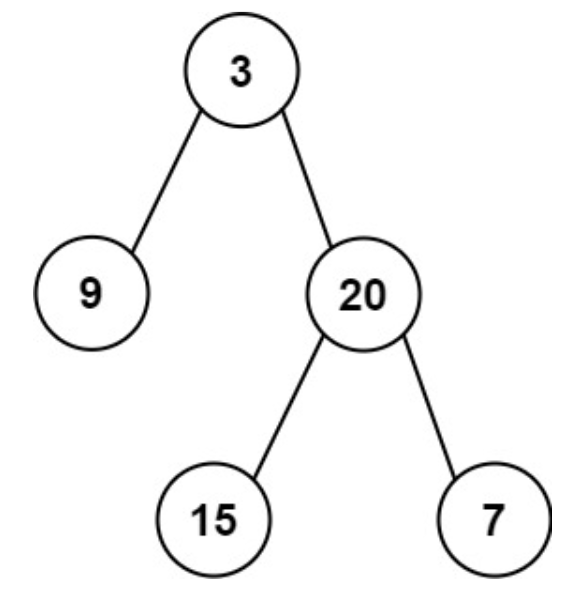
也就是必须考虑左子树就是一个叶子结点的情况，如果不画成上面这种也就是左子树不是一个叶子结点很容易将代码写成：

int sumfun(Node* node) {
    if (node == nullptr) return 0;
    if ((node->left == nullptr) && (node->right == nullptr)) return 0;
    if ((node->left->left == nullptr) && (node->left->right == nullptr)) {
        return node->left->data_;
    }
    int left = sumfun(node->left);
    int right = sumfun(node->right);
    int sum = left + right;
10　　　return sum；
}

这个代码一旦遇到左子树是一个叶子节点的情况就直接将左叶子结点返回了，而没有考虑右子树中的左叶子结点

正确的代码如下：

 

int sumOfLeftLeaves(Node* node) {
    if (node == NULL) return 0;
    if (node->left == NULL && node->right == NULL) return 0;

    int leftValue = sumOfLeftLeaves(node->left);    // 左
    if (node->left && !node->left->left && !node->left->right) { // 左子树就是一个左叶子的情况
        leftValue = node->left->data_;
    }
    int rightValue = sumOfLeftLeaves(node->right);  // 右

    int sum = leftValue + rightValue;               // 中
    return sum;
}