SIFT

一些基础：

图像的一阶导数和二阶导数

一阶

梯度指出了最大变化率以及产生最大变化率的方向

参考文章：

(103条消息) 【opencv】18.数字图像一阶导数、二阶导数的数学原理_二阶导数图像_Mister Zhu的博客-CSDN博客

二阶

直接用二阶模板和图像进行卷积

边缘检测：

高斯一阶导求边缘

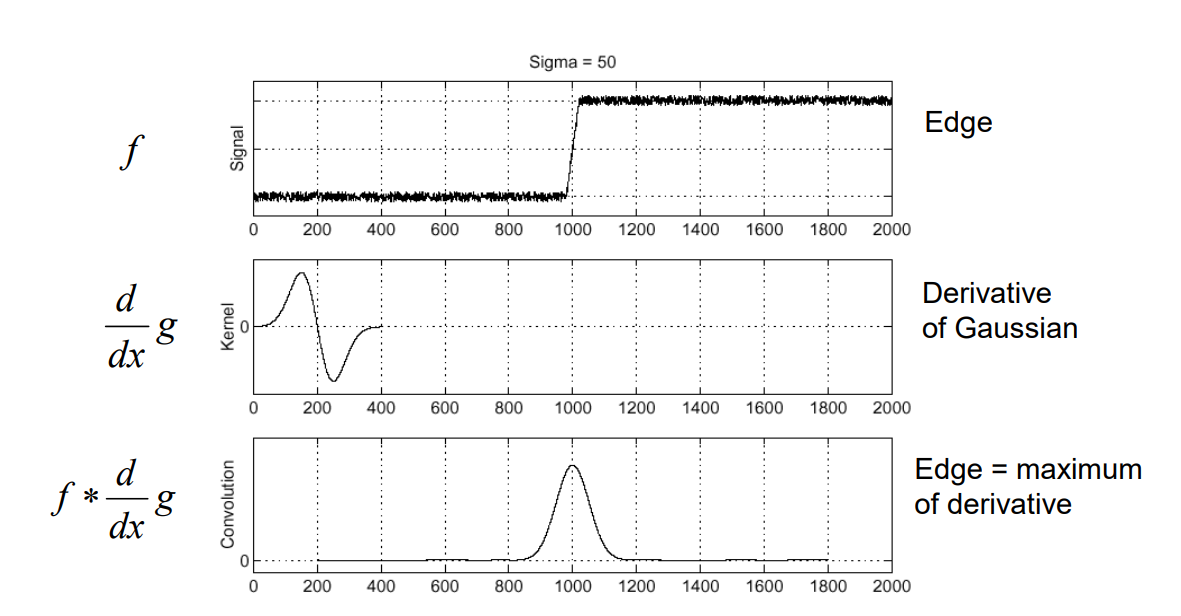
   1.一个图像卷积高斯一阶导这意味着做了两件事情：

• • 对图像进行高斯模糊
  • 对高斯模糊的图像求一阶导

　　 2.这些一阶导数取极值的地方就是边缘

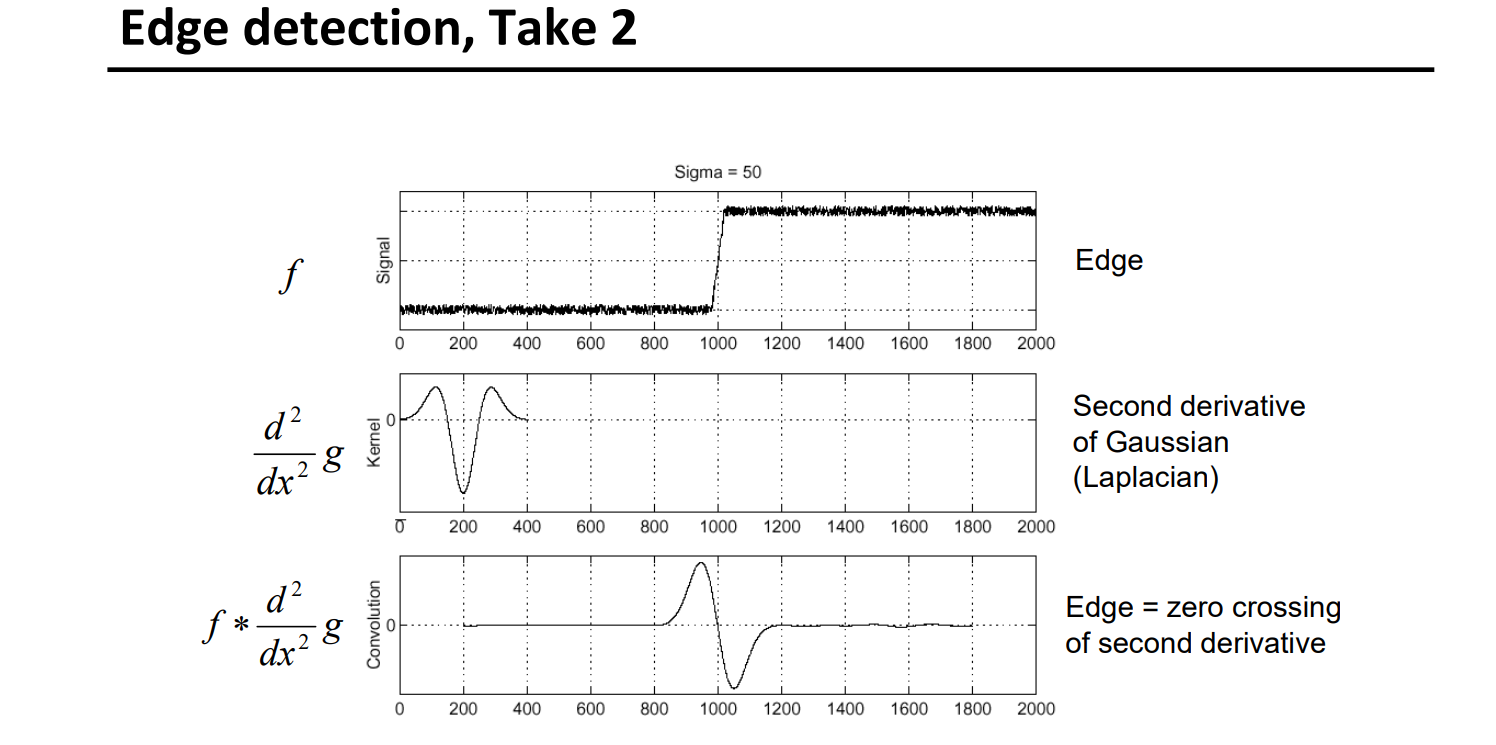
同理，高斯二阶导（也称为拉普拉斯核)为0的地方就是边缘(二阶导数为0，一阶导数取极值)

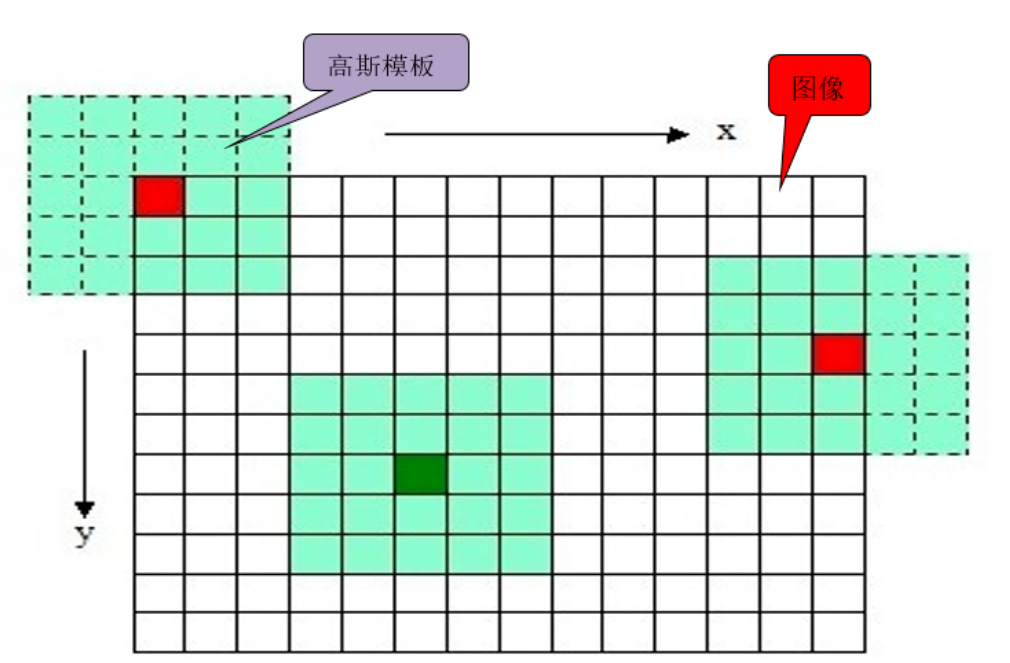
高斯核的方差σ和高斯核的窗口大小的关系：

根据3σ原则

高斯核的方差和信号响应的关系

上图表明信号和高斯核匹配的时候就能产生极值(原理有空了解下)

我们实际运用的时候是信号尺度未知，我们采用不同方差的高斯核核信号匹配，但是这会带来一些问题

 

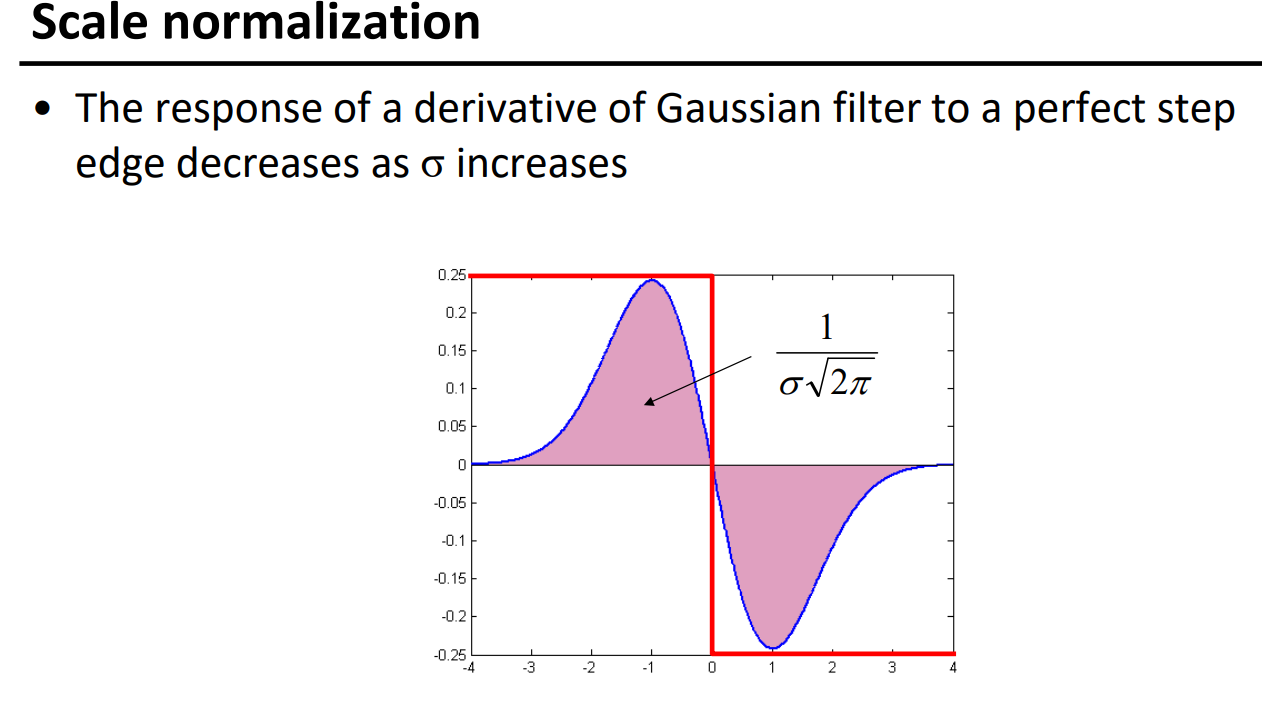
如果我信号的幅值当成1的话，信号和高斯卷积后的面积，就会随着方差的增大而越来越小，导致我们找不到极值

因此我们要做尺度归一化，也就将所有的响应值乘以方差σ，这是一阶的情况，二阶就要乘以σ²(1/σ√2Π，怎么来的了解下)

最后只需记住当卷积核的尺寸(由σ决定)和信号匹配的时候，信号能得到一个响应极值。

面积最大化的情况(之后再去理解)

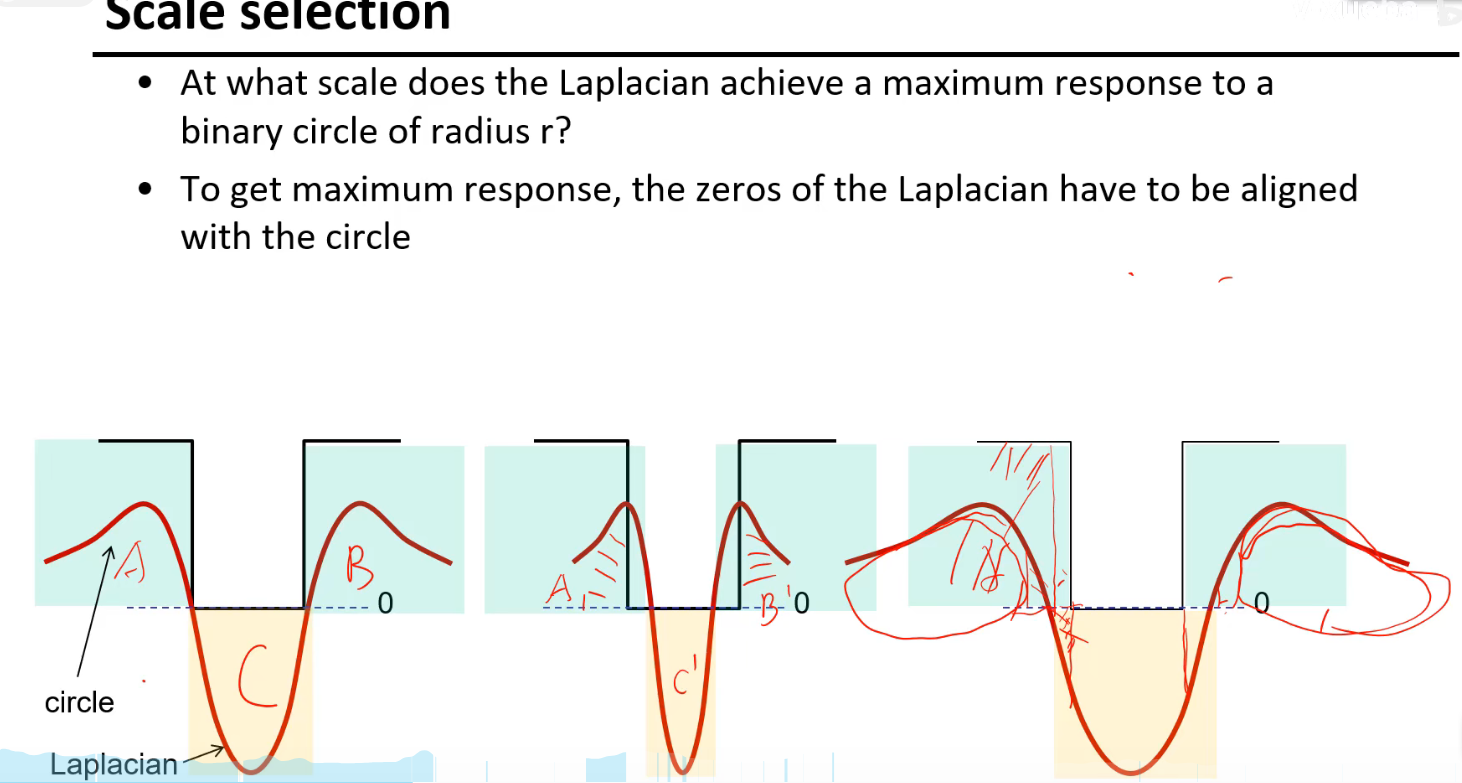
只有第一种情况：信号正好嵌入这个沟中，红线和黑线(信号)相乘的结果和x轴围成的面积才是最大的

嵌进去的一半的长度就是下图中的圆的半径

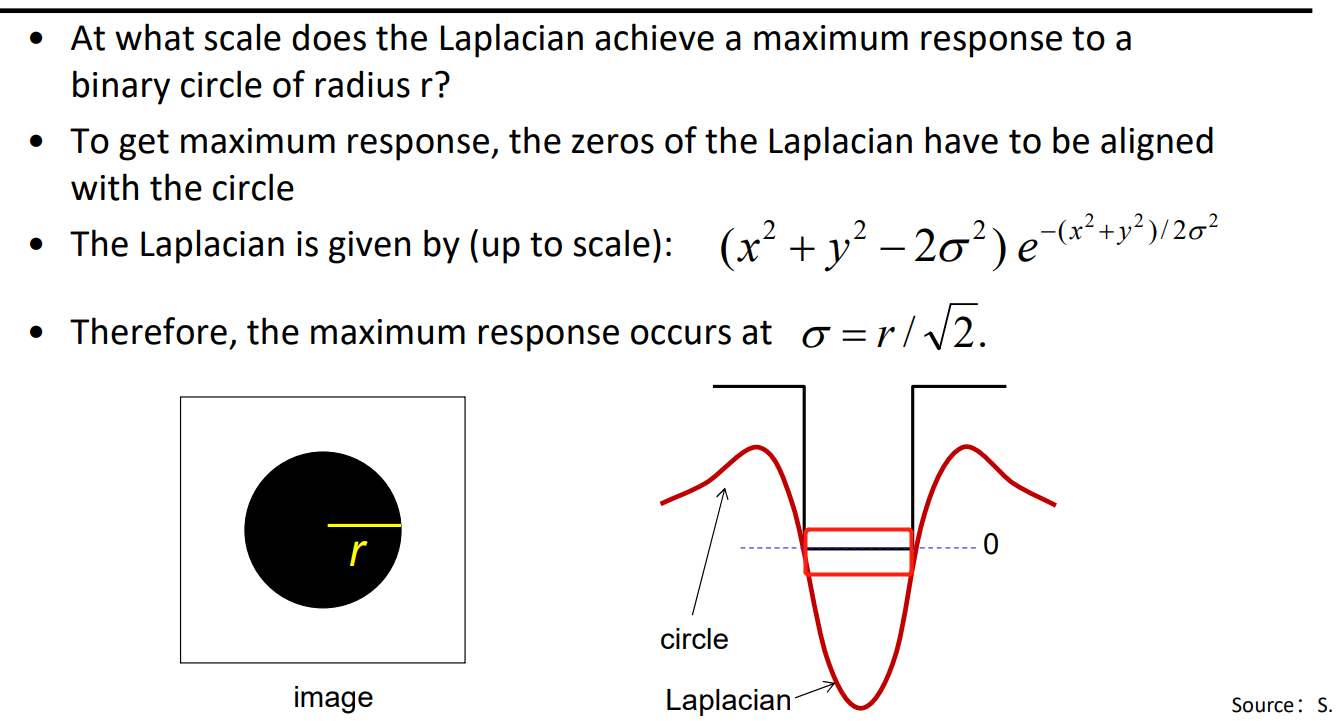
这个圆方程就是使这个二维拉普拉斯算子为0求得的，即x²+y²=2σ²半径就是√2σ，也就是那个红框内一半的长度，也就是信号

SIFT算法：

根据上述可知匹配圆的半径为√2σ

 

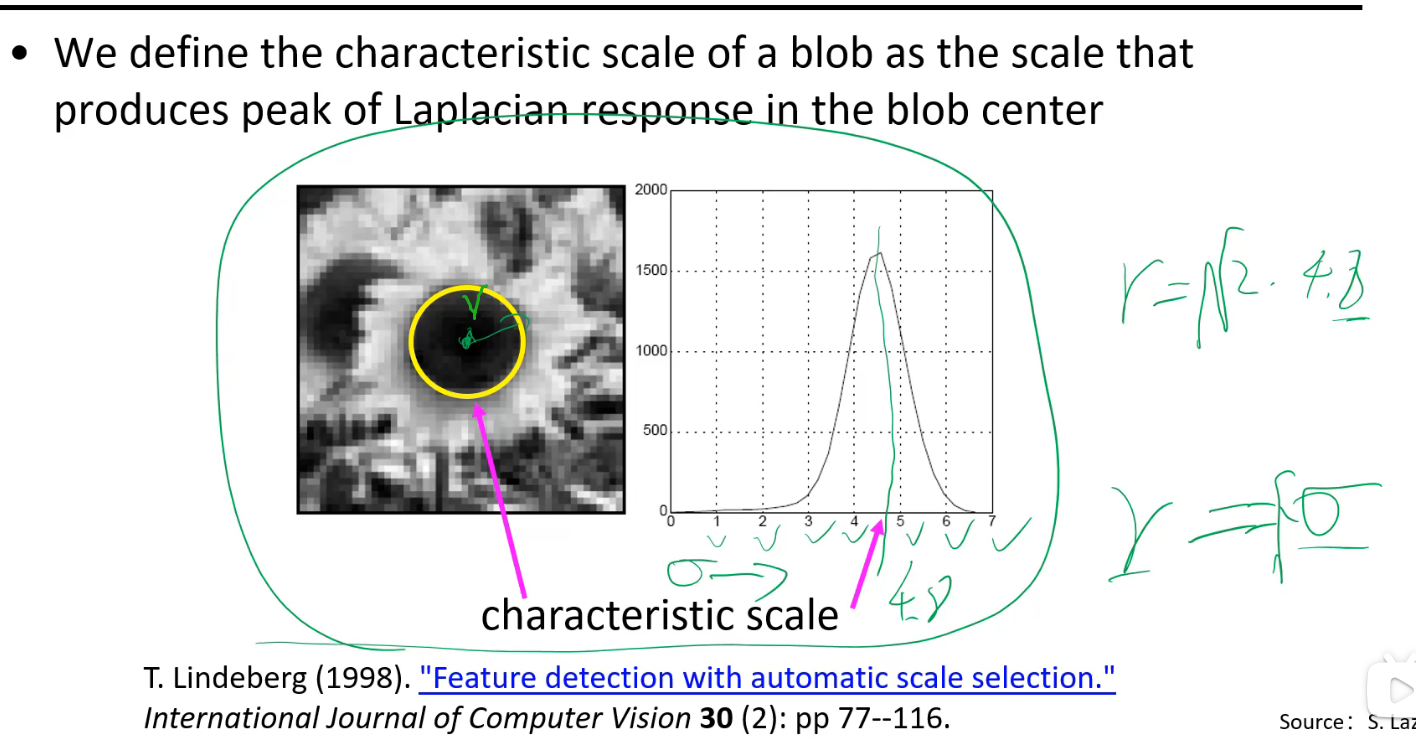
尺度不变性：

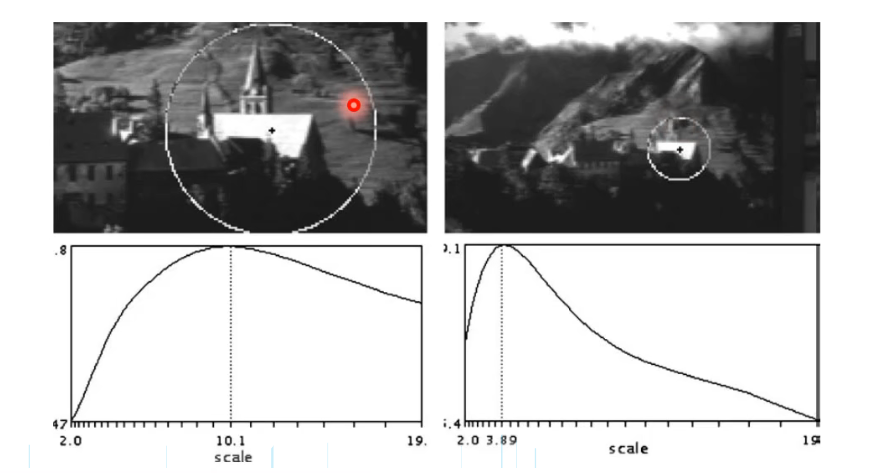
该图可以看到大尺度的和小尺度的同样可以匹配得上

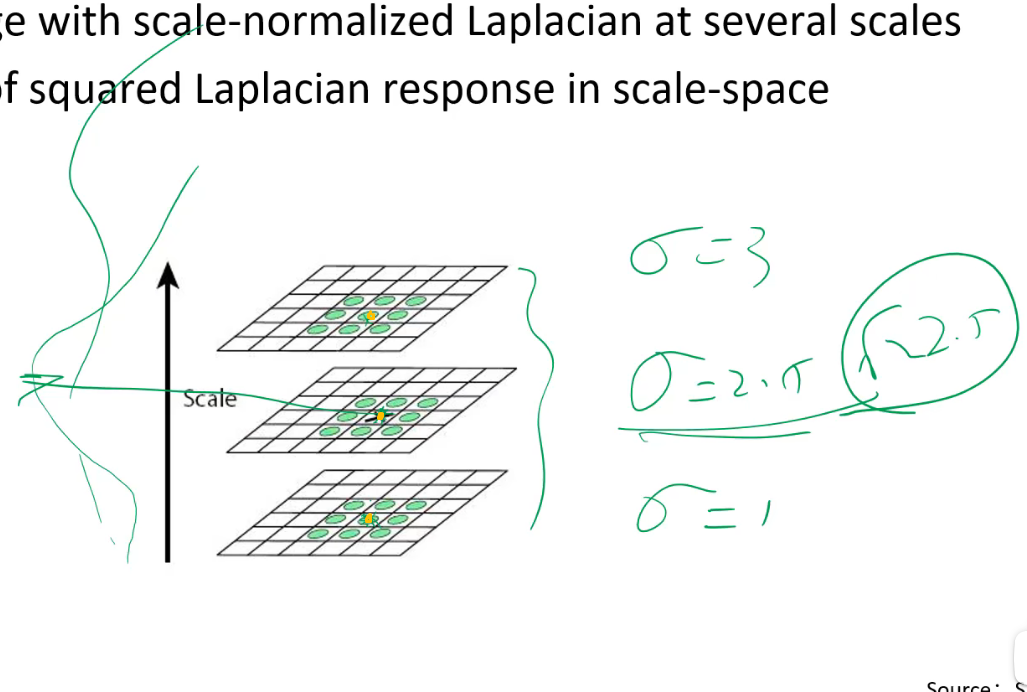
三个黄色的点中哪个响应函数值最大，就用哪一点所在那一层的σ就求匹配圆的半径。

问题是

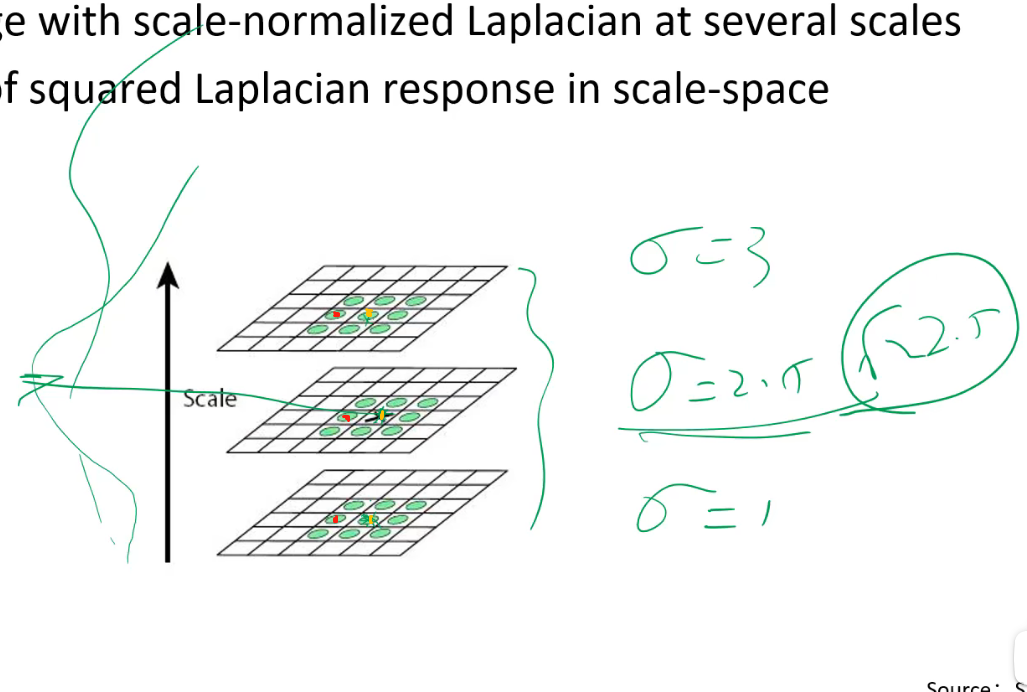
当我中间层的红色的点是三个红点最大的我确定一个匹配圆，当中间的黄色点是三个黄色点中最大的我确定一个匹配圆，而相差一个像素的两个像素几乎是描述同一个东西，因此这就导致了同一个东西对应了同样大小的两个圆，这显然是没必要的，因此采用极大抑制。

如果某一点在这三层邻域内的27个点(这里的27表示我们有三层，如果有4层的话就是36了)中所对应的响应函数值最大，那么就取那个点所在层的σ去计算匹配圆的半径,但是这个点不能来自边界层，也就是只能在中间那层选

拉普拉斯算核(也就是高斯的二阶导)计算量太大，随着σ的增大，模板的窗口大小也增大，大到我几乎要算一个像素点的响应值的时候我几乎要将整个图像的像素点都要和拉普拉斯模板卷积一下。

我们采用高斯差分核

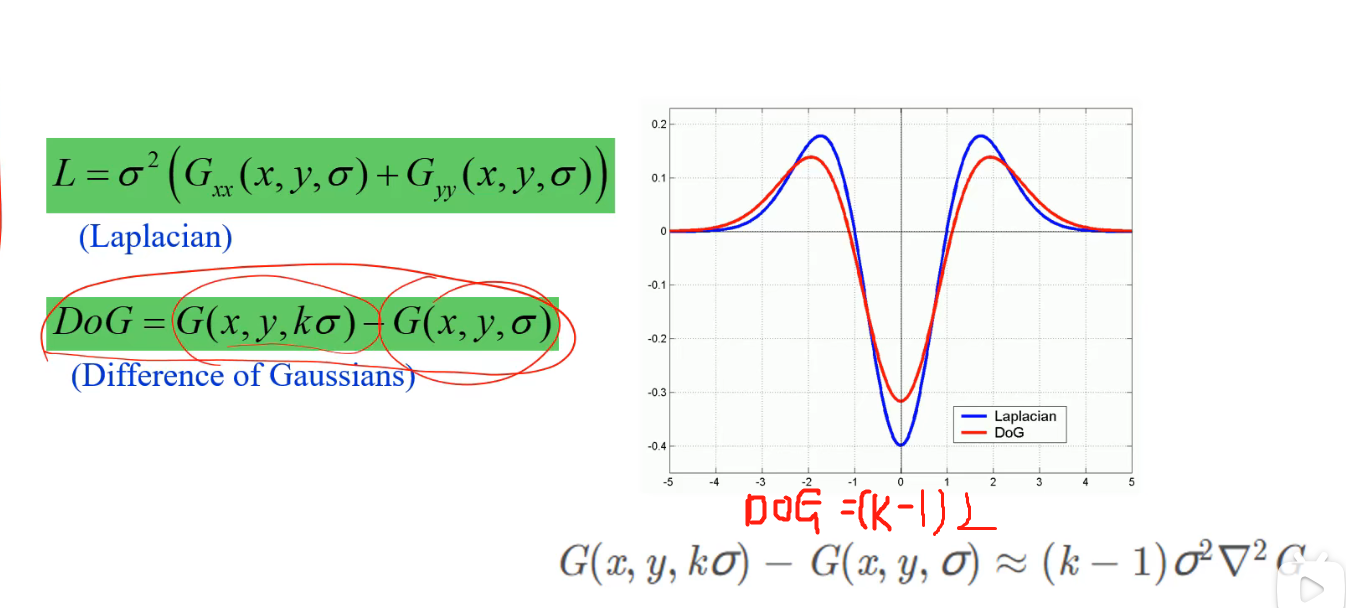
实现步骤：

高斯差分金字塔的建立:

高斯金字塔的建立：

1.层数和组数的确定：

——————————————————————————————————————

备注：

n的含义：

假设高斯金字塔每组有S = 5层，则高斯差分金字塔就有S-1 = 4层，那我们只能在高斯差分金字塔每组的中间2层图像求极值(边界是没有极值的)，所以n = 2

——————————————————————————————————————

 

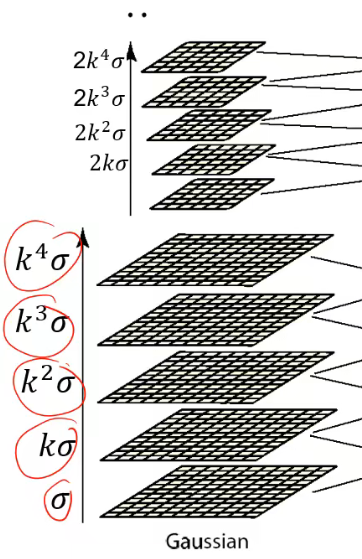
2.每组的图像尺寸的确定

对原图进行降采样处理得到高斯金字塔的第二组图像的尺度，对第二组的图像进行降采样得到第三组的尺度，依次类推。降采样的意思是隔点取样。

3.每组中每层的尺度确定

 

4.高斯金字塔的每层的图像怎么获得：

第一组第0层：

高斯核的尺寸＝大于6σ₀+1的第一个奇数。

高斯核的每个元素确定：

                   σ=σ₀

最终的图像使用高斯核和原图像卷积

第一组第1层：

将第一组第0层得到的图像与方差为的高斯核进行卷积

第一组第2层：

将第一组第0层得到的图像与方差为的高斯核进行卷积

.....以此类推

第二组第0层：

为上一组倒数第3层降采样所得，其他层还按照第二组的方法求得。

在这里我们理解下高斯金字塔：

 

Q1：什么是图像高斯金字塔？

 

A1：在说高斯金字塔之前，我们先来说一下人的眼睛，我们人眼对世界的感知有两种特性：一是近大远小：同一物体，近处看时感觉比较大，远处看时感觉比较小；二是"模糊"：更准确说应该是"粗细"，我们看近处，可以看到物体的细节(人会觉得比较清楚)，比如一片树叶，近看可以看到该树叶的纹理，远处看只能看到该片的大概轮廓(人会觉得比较模糊). 从频率的角度出发，图像的细节(比如纹理，轮廓等)代表图像的高频成分，图像较平滑区域表示图像的低频成分.

 

图像高斯金字塔实际上是一种图像的尺度空间(分线性和非线性空间，此处仅讨论线性空间)，尺度的概念用来模拟观察者距离物体的远近程度，在模拟物体远近的同时，还得考虑物体的粗细程序.

 

综上，图像的尺度空间是模拟人眼看到物体的远近程度以及模糊程度.

 

图像高斯金字塔就考虑了这两个方面：① 图像的远近程度；② 图像的模糊程度(理解为粗细更好).

 

Q1：那该怎么模拟图像的远近程度呢？

 

A1：采样法(上采样，下采样)

 

比如一幅图像，对于每一行，隔一个像素点取一个像素点，那么最后得到的图像就是原图像的行和列各1/2. 这属于下采样的一种.

 

Q2：那该怎么模拟图像的粗细程序呢？

 

A2：采用高斯核对图像进行平滑处理，因为高斯卷积核是实现尺度变换的唯一线性核.

因此高斯金字塔的建立就体现出了尺度不变性，因为它将各种尺寸的图像，各个图像尺寸下的各个尺度(也就是不同方差的高斯核卷积的模糊程度)全都考虑进去，而从中选出的极值点。因此它对不同图像的尺寸和模糊程度具有鲁棒性

高斯差分金字塔的建立：

就是高斯金字塔每两层对应像素做差所得的图像

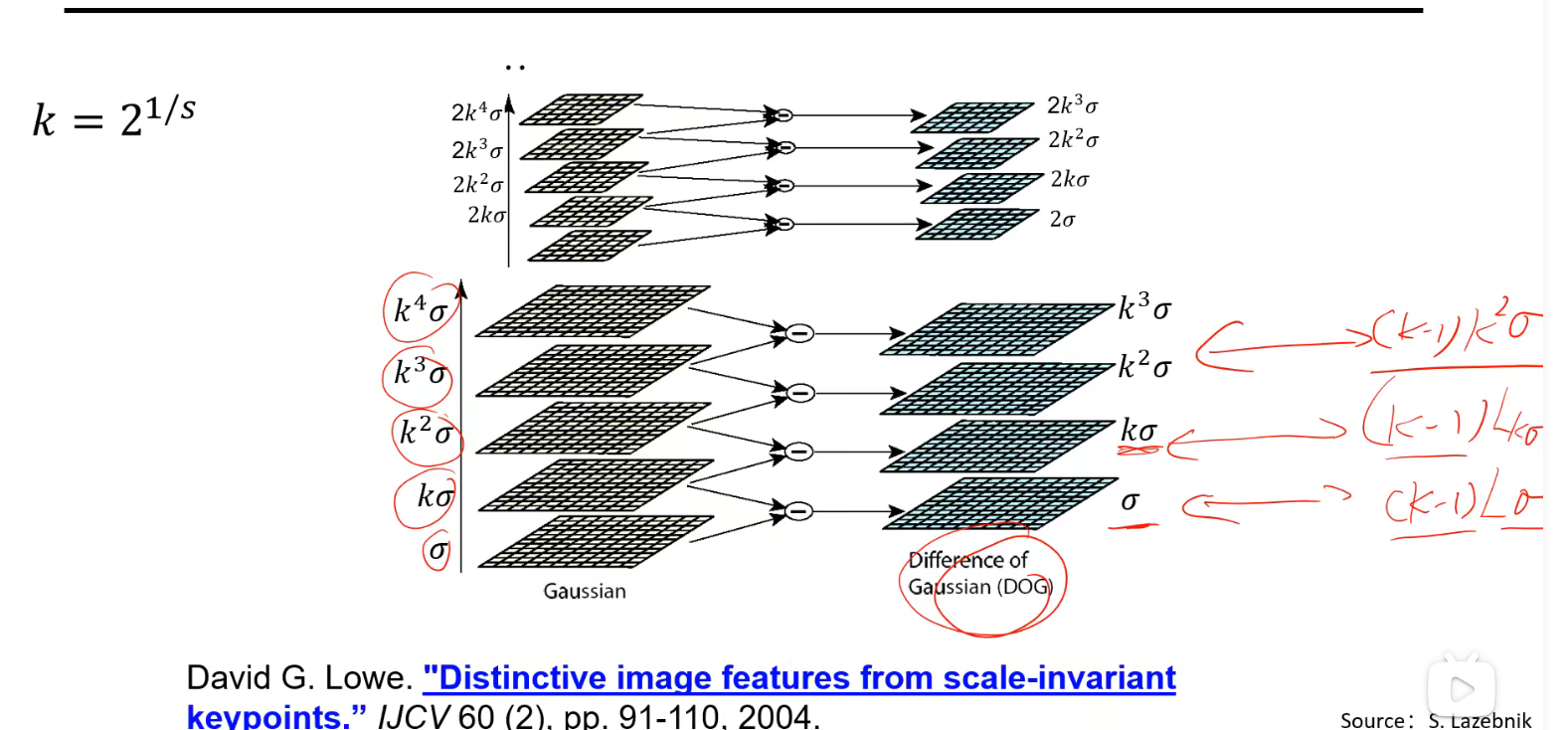
高斯差分金字塔的连续性：

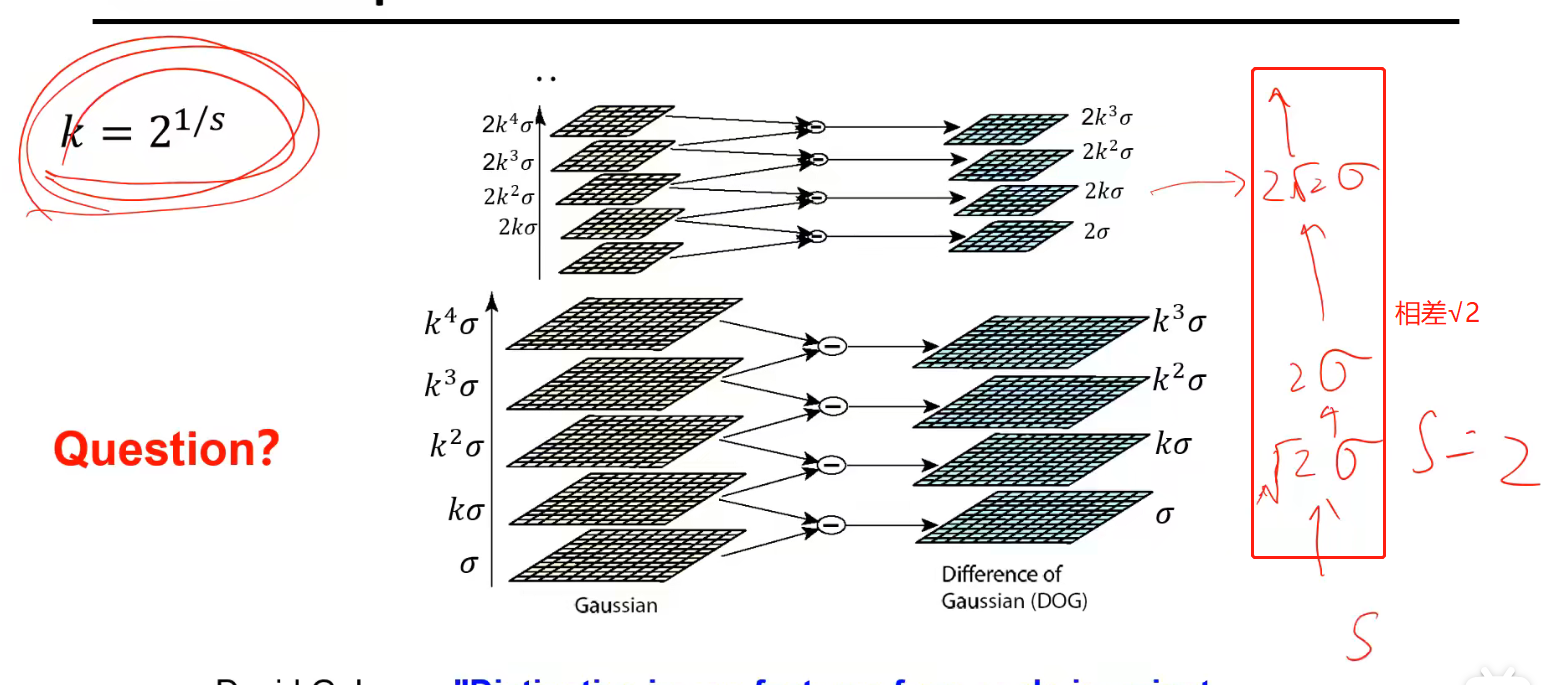
关键点的确定：

这里以下图为例：

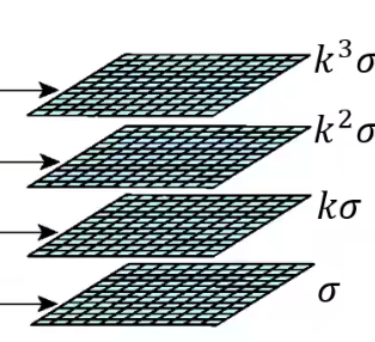
中间两层中每一个像素为中心选取周边邻域的9个点进行比较，也就是一层9个，2层18个。比较这18个点哪个点值最大就以这个点为中心，这一层的方差值为半径画个圆，比如说kσ为半径画个圆。

寻找亚像素极值：

当我们检测到极值点之后，会发现一个问题，高斯差分金字塔是离散的(因为尺度空间和像素点都是离散的)，所以找到的极值点不太准确的，很大可能在真正极值点附近(达到亚像素精度)，同时去除低对比度的关键点和不稳定的边缘响应点(因为DOG算子会产生较强的边缘响应)，以增强匹配稳定性、提高抗噪声能力。

亚像素极值点的获取如下：

下图中f是值关键点的响应值

 当任一维度上的值小于0.5时（即x或y或 σ），终止迭代，否则：

在Lowe论文中中进行了5次迭代终止算法。

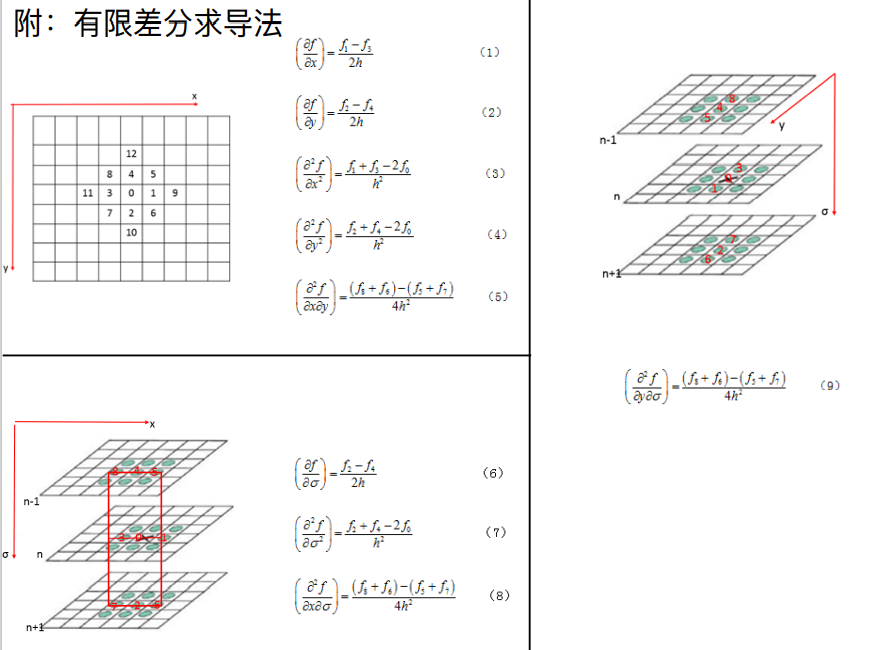
上面的图片所有异界偏导和二阶偏导都少一个， h一般取1

舍去过小的点

另外，过小的点易受噪声的干扰而变得不稳定，所以将小于某个经验值(Lowe论文中使用0.03，RobHess等人实现时使用0.04/n)的极值点删除。