极几何

三角化及其求解方法：

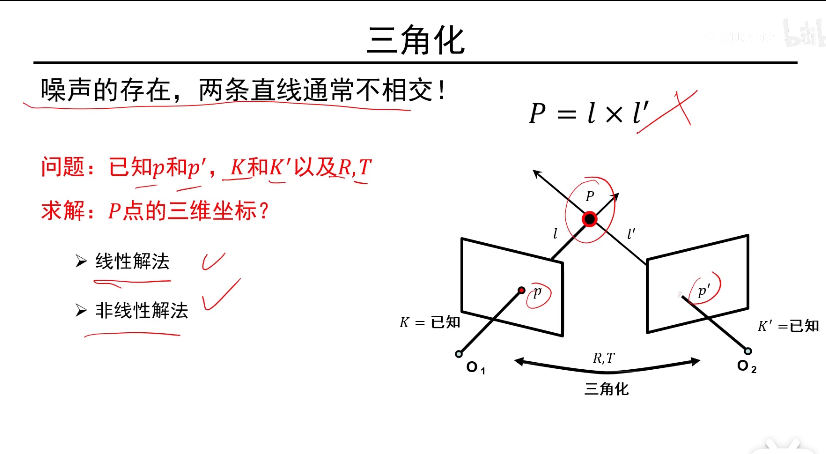
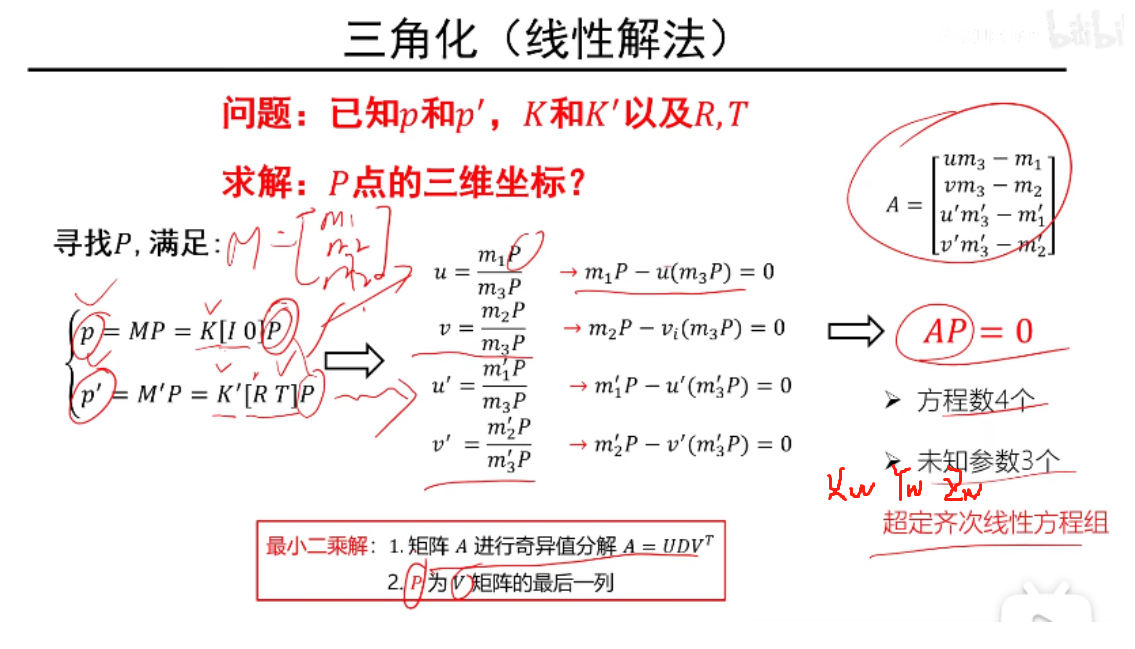
说明：以相机1相机坐标系为世界坐标系

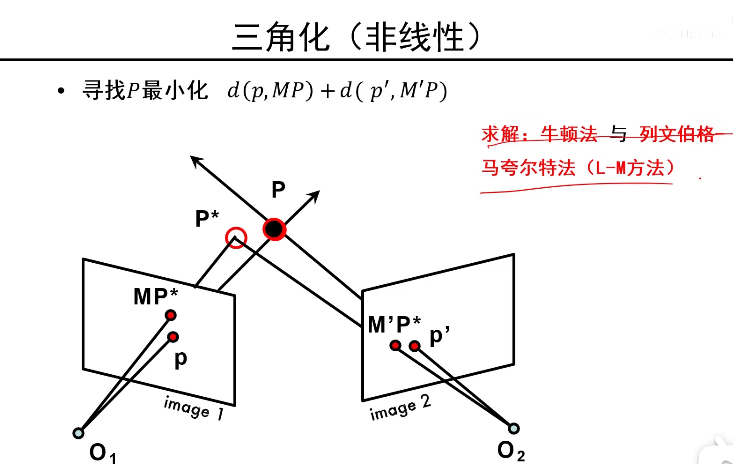
构建能量函数使物点在两个相机上的投影点和真实的点之间的距离最小

使用LM等最优化算法对实现上述表达式的最小化

多视几何

上述问题在实际应用中：

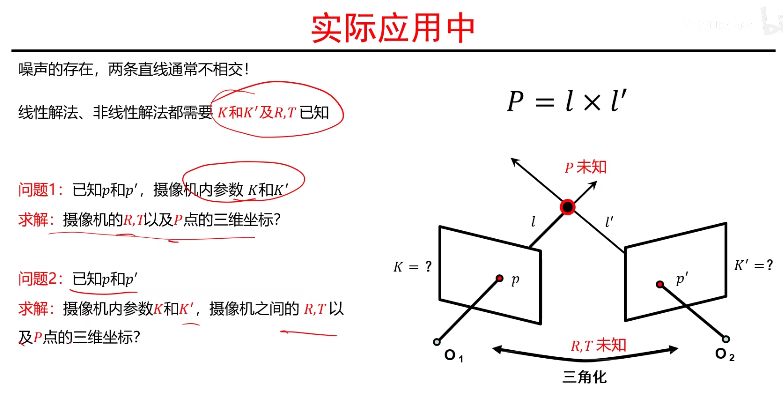
实际情况下我们不知道p和p'是对应点

极几何

极几何与左相机的成像点p匹配的p'，一定在右相机的极线l'上，l'是p的对极线，它描述了同一场景下或则同一个物体的两个视点图像间的对应的几何关系，多视图几何解决的就是这样的问题，也就是已知一个图像中的p点，如何在另外的图像中找到p'点。

物点一定在射线O₁p上，O₁p在右相机的投影是l'，因为物点在射线上那么物点的投影一定在l'上

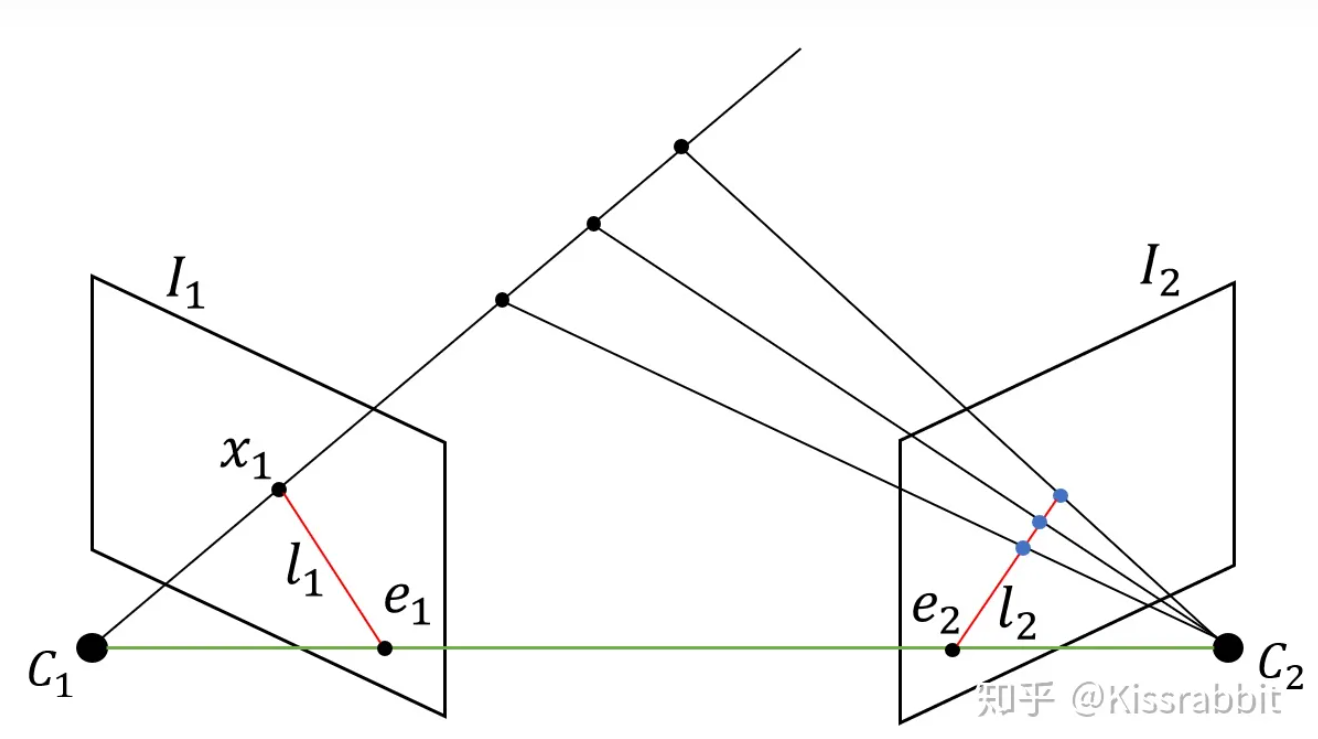
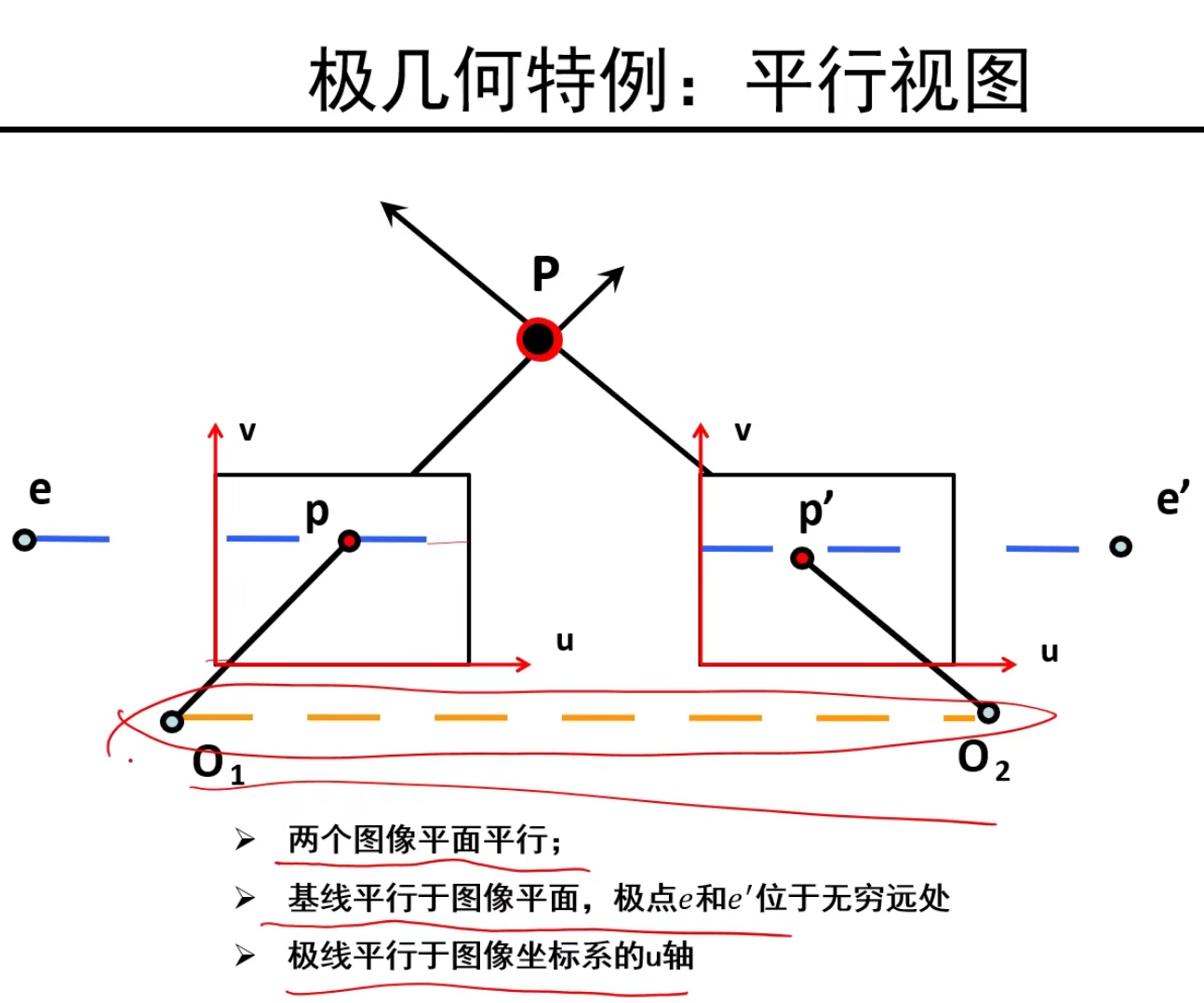
O₁O₂这条直线和两个成像平面底下的两条边平行，因此交点在无穷远处，两个交点是极点

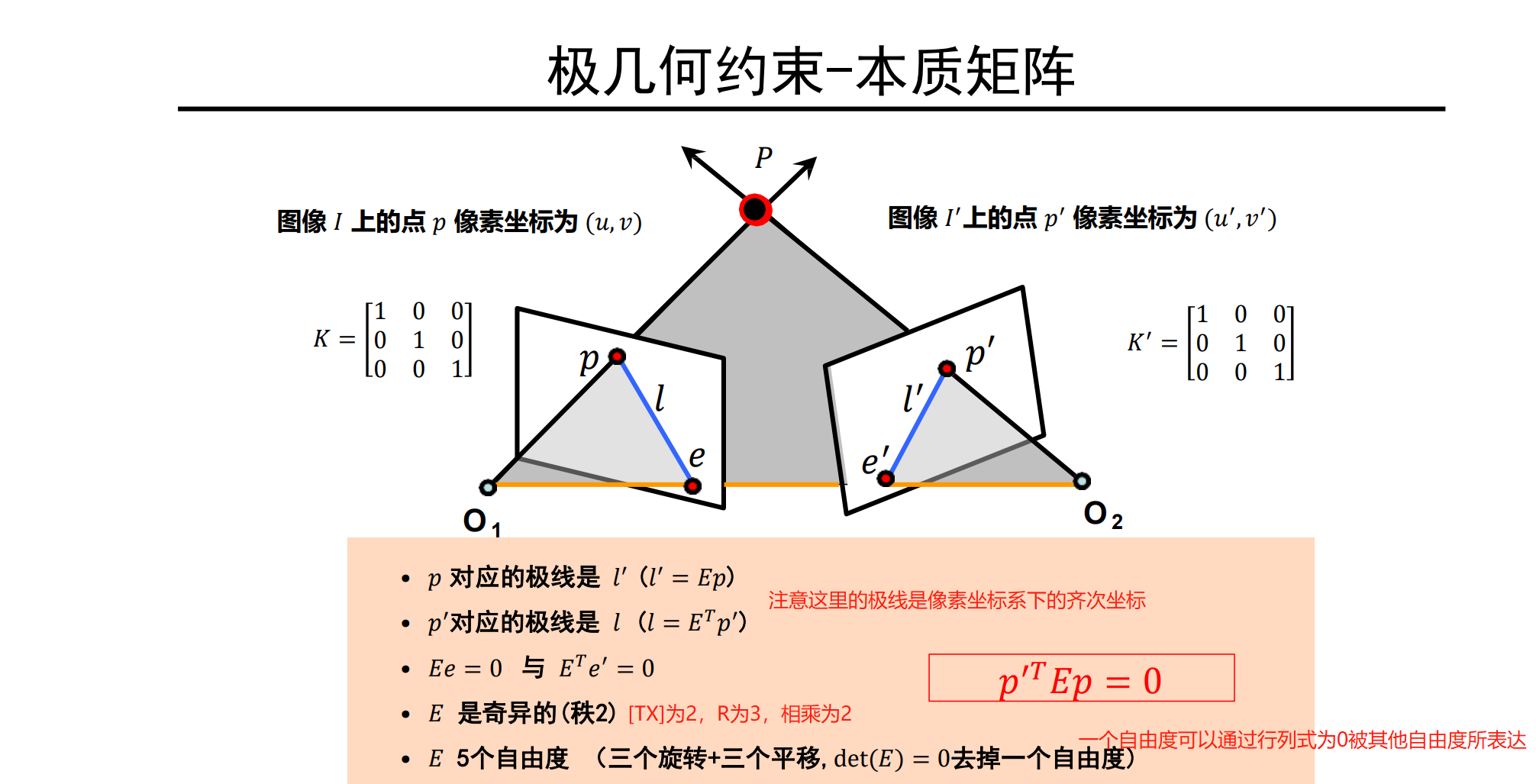
本质矩阵

本质矩阵对规范化摄像机拍摄的两个视点图像间的极几何关系进行代数描述

 

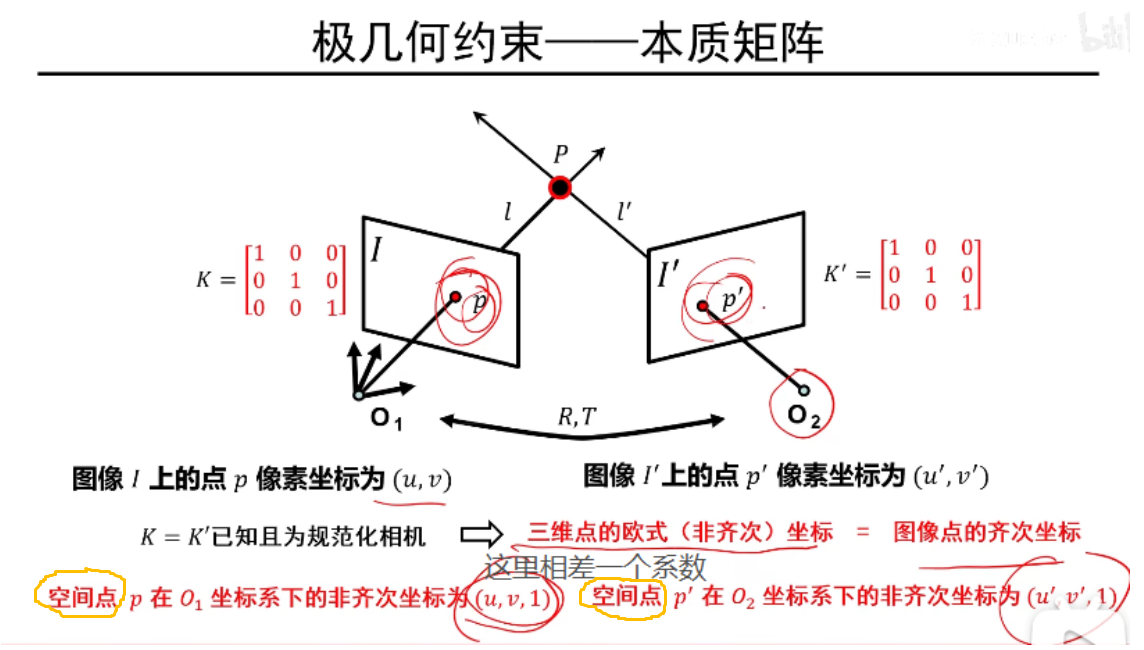
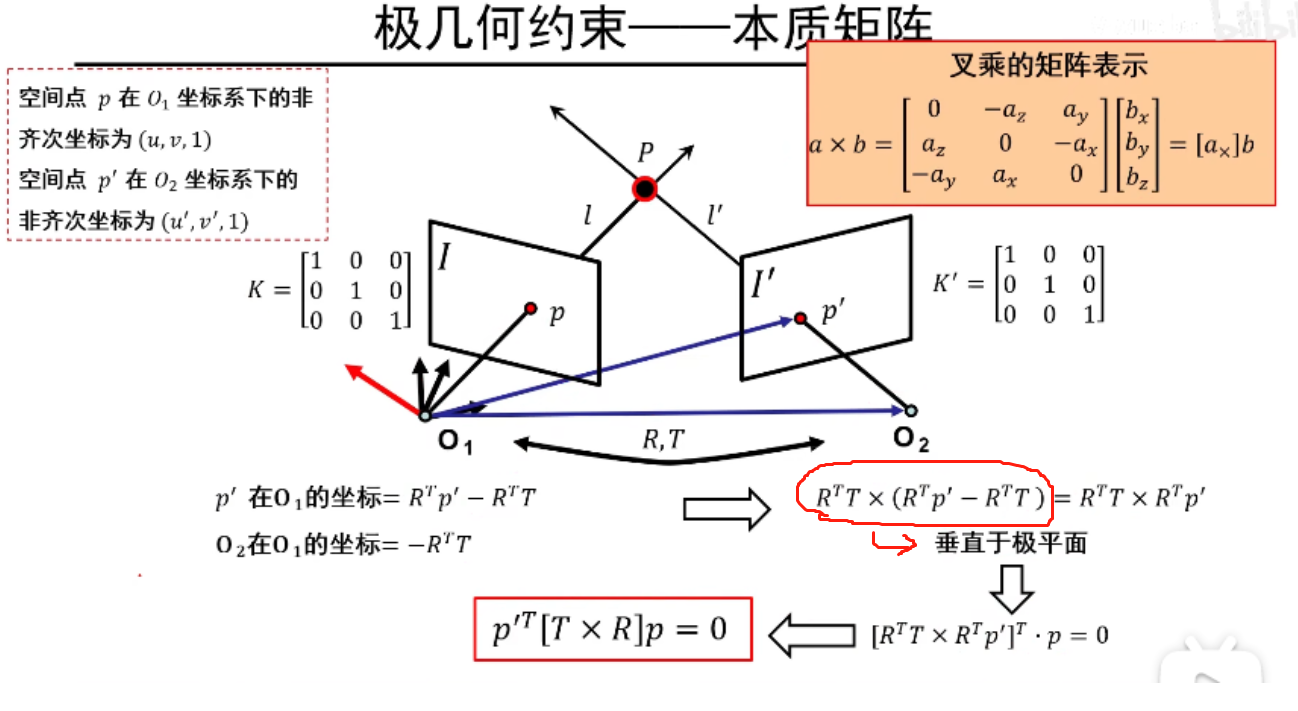
核心就是首先推出p,p'点在相机坐标系下的关系，然后利用规范化摄像机的二维点的齐次坐标(像素坐标系下)和三维点(相机坐标系下)的欧式坐标相差一个系数的性质得出这两个点三维的欧式关系也是这两个点的二维的齐次关系，从而得出这两个点的二维齐次关系

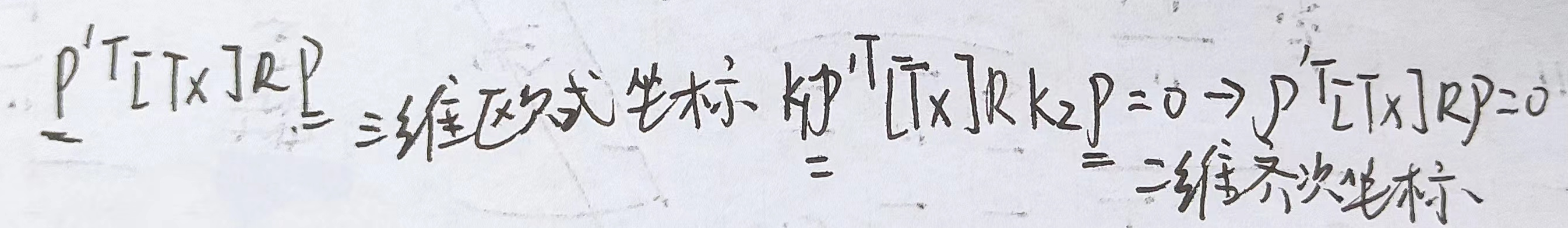
k₁,k₂为相差的系数

因此利用上式可直接带入p的像素坐标系下的齐次坐标求p'的像素坐标系下的齐次坐标

基础矩阵

基础矩阵对一般的透视摄像机拍摄的两个视点的图像间的极几何关系进行代数描述

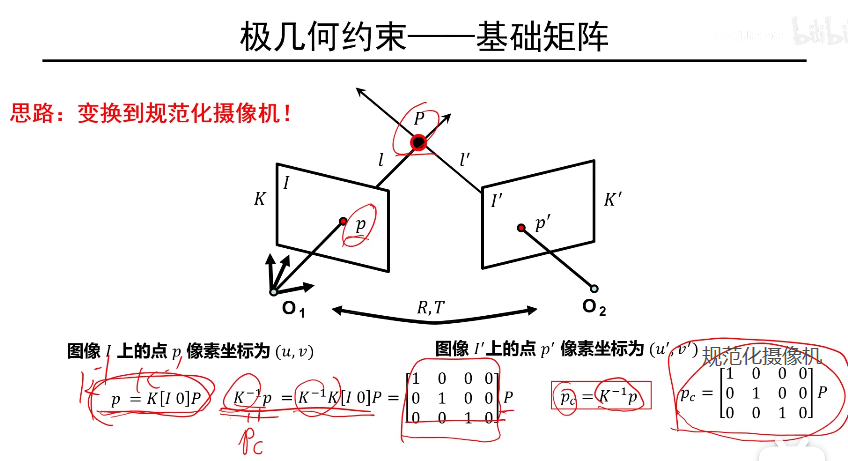
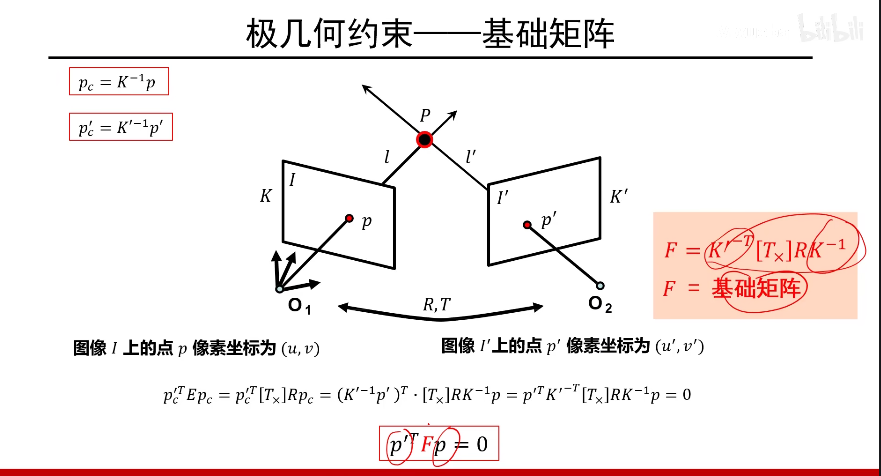
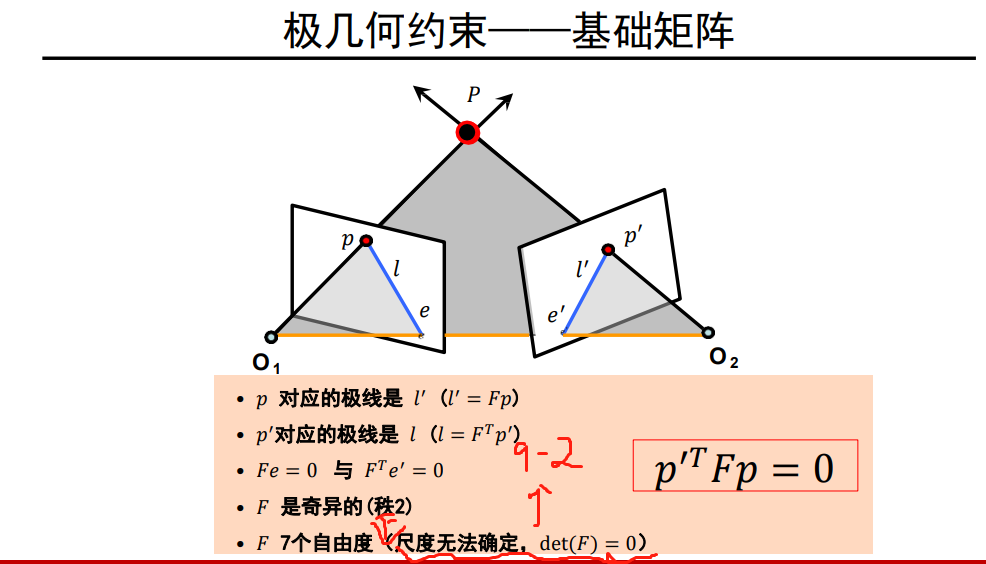
纯平移运动的定义是没有旋转，即旋转矩阵为单位阵，这时F矩阵会退化为一个三阶反对称阵，反对称矩阵有3个未知数，加上一个不可逆的约束，因此自由度为2；纯平面运动的定义是平移方向和旋转方向垂直，因此添加了这样一个约束，因此自由度在7的基础上减1变成6。

基础矩阵F的求解

八点法求基础矩阵

 

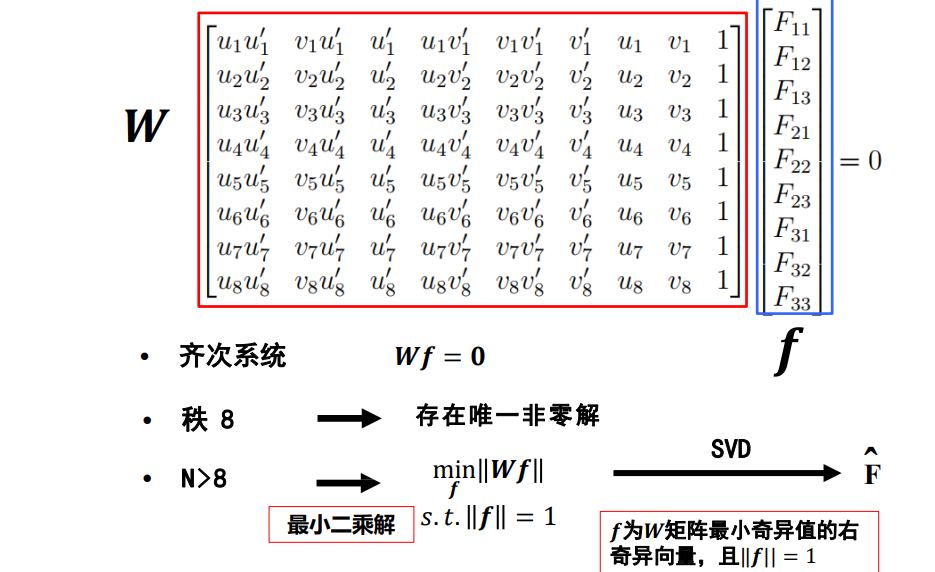
像素坐标的跨度太大，比如一个1920*1080的图像，这就导致我们可能选取的坐标有一两个过大，其他的都很小，这就导致较小的奇异值都很接近

此时我们使用归一化的八点法来消除上述的影响

——————————————————————————————————————————————————

备注：

将一组数据归一化均值为a,方差为b的方法是

——————————————————————————————————————————————————

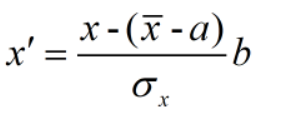
T或T'的计算公式为：

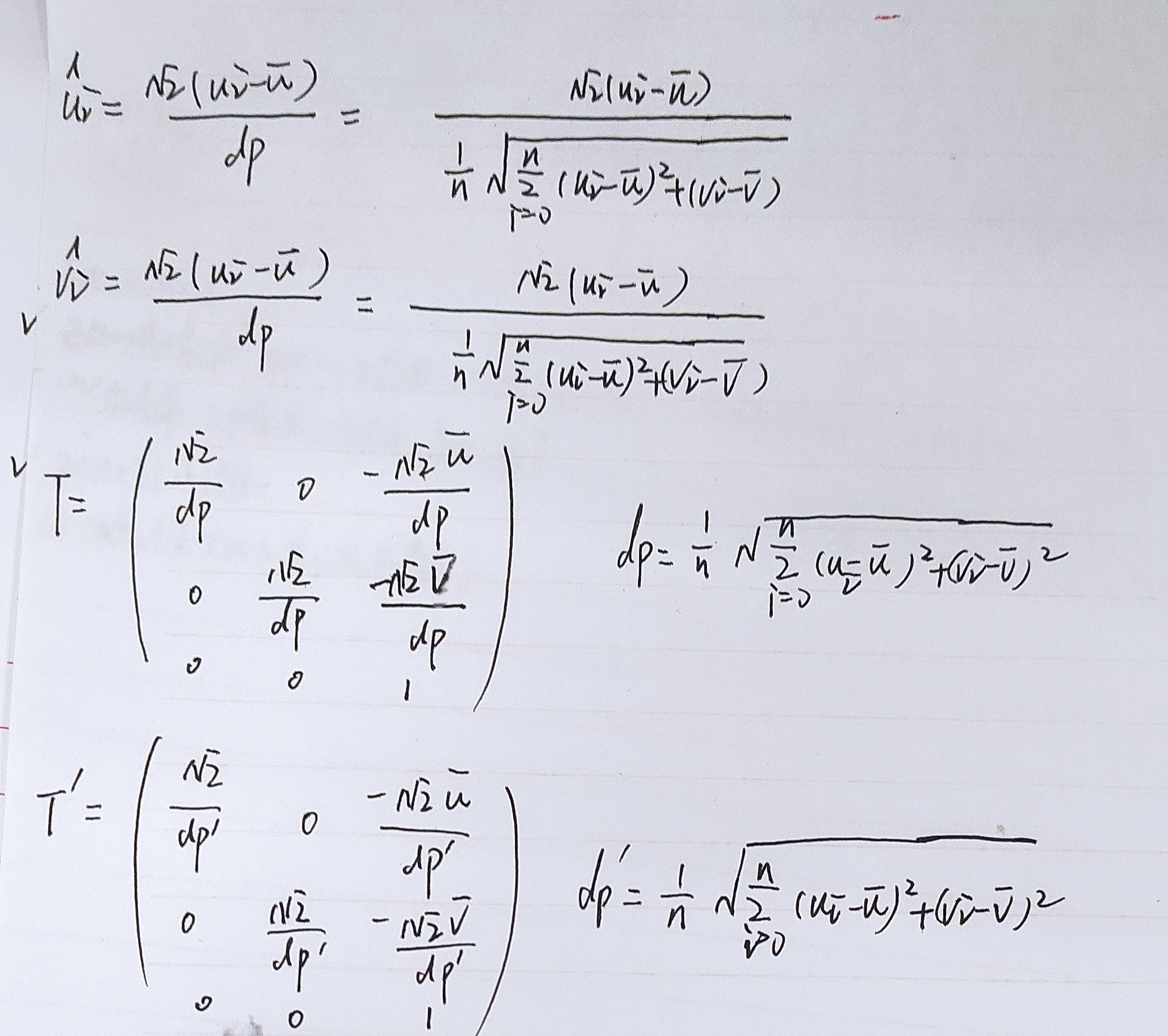
一维归一化是减均值除以方差，二维归一化是是减均值除以平均欧式距离。

参考文章：

In defence of the 8-point algorithm（八点算法的归一化（规则化）详解）基础矩阵_八点算法和归一化八点算法_三眼二郎的博客-CSDN博客

单应矩阵

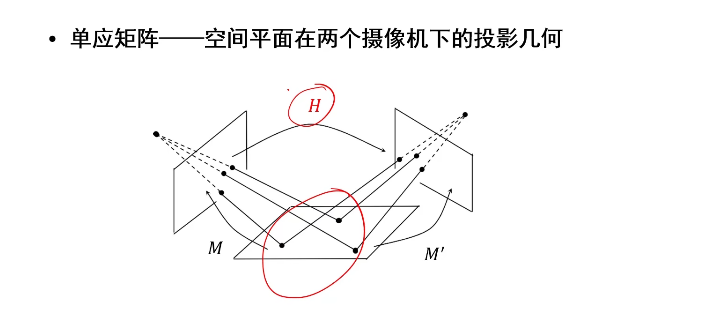
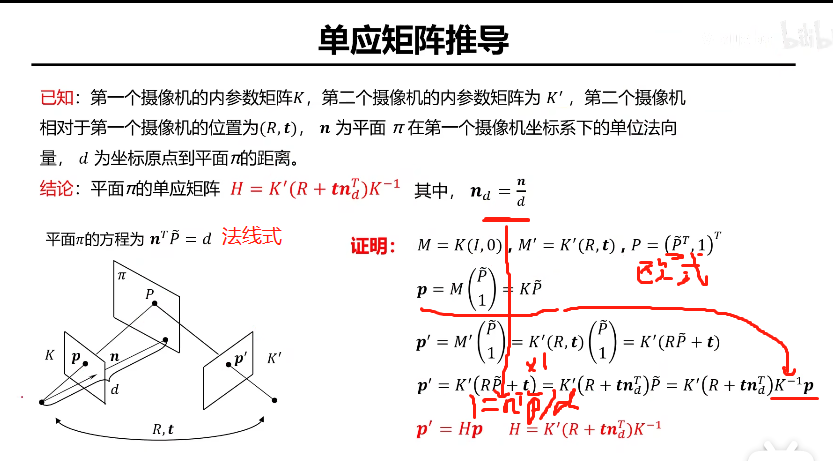
R为第一个相机到第二个相机的旋转矩阵，t为第一个相机到第二个相机的平移矩阵

----------------------------------------------------------------------------------------------------------

备注：

法线式方程：
已知平面在第一个相机坐标系下的一般方程为Ax+By+Cz+D=0

则法向量为(A,B,C)^T，法向量单位化(A,B,C)^T/(A²+B²+C²)^1/2

点到平面的距离公式为

则原点到平面的距离是将x₀=0,y₀=0,z₀=0

----------------------------------------------------------------------------------------------------------

从单应矩阵的表达式可以看出，单应矩阵描述的是真实世界中所有物点在同一平面这个前提下(所有点不在同一平面就没有n_d，因为你连平面都没有了，没有n_d就构不成单应矩阵)两个匹配点的对应关系。

可以先估计出单应矩阵然后可以根据上图的红色表达式求出相机的内外参数

 

单应矩阵的求解

 

本质矩阵基础矩阵与单应矩阵

点与点之间齐次坐标的关系，点与线齐次坐标的关系