图总结

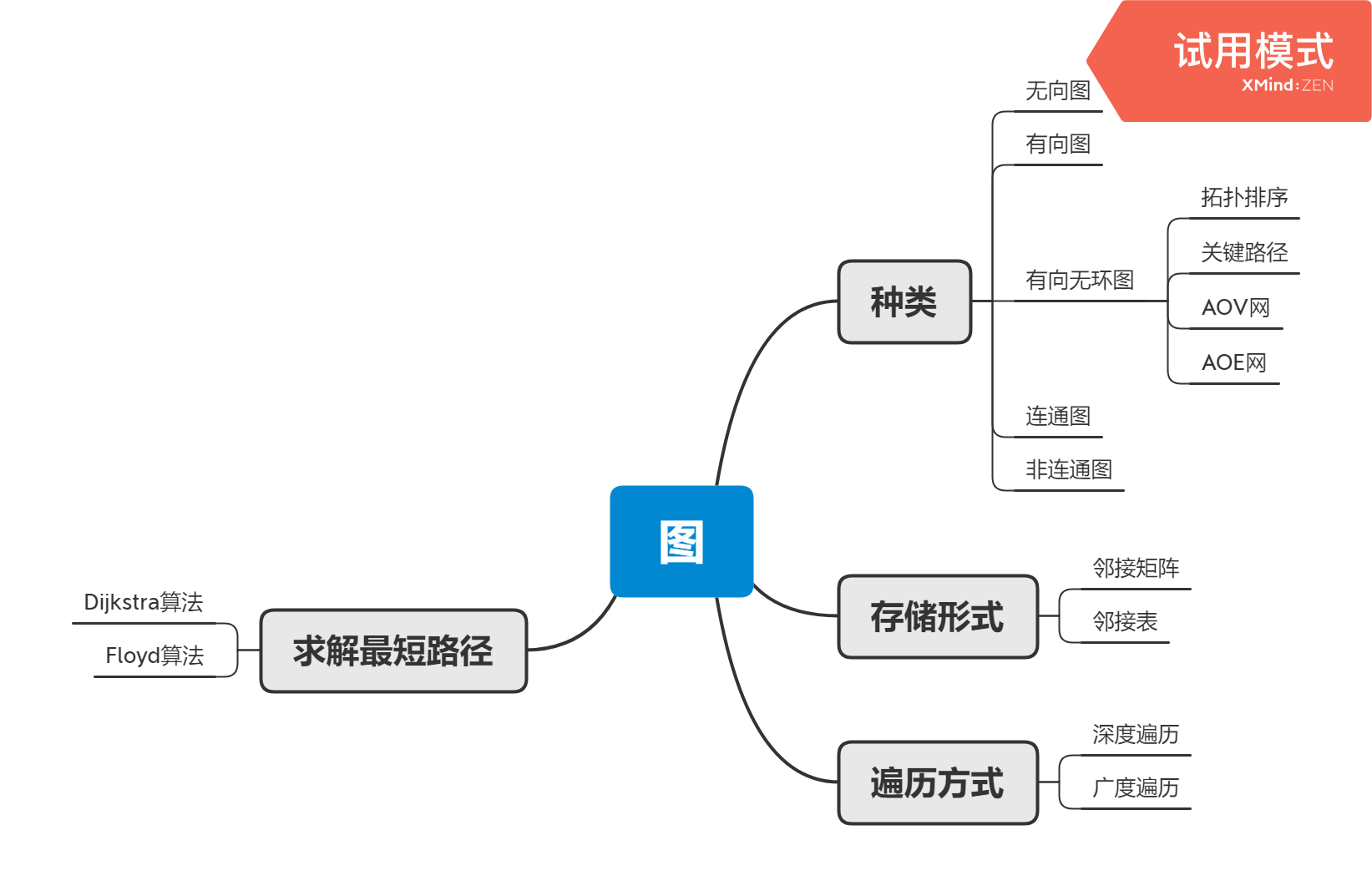
种类

无向图

最多有n（n-1）/2条边，这种无向图被称为完全图
连通图：无向图的任意两点之间都是连通的
连通分量：极大连通子图

有向图

最多有n（n-1）条边，这种有向图被称为有向完全图
强连通图：有向图的任意两点之间都是连通的，各个顶点均可到达
强连通分量：极大连通子图
有向图顶点的度是顶点的入度和出度之和

存储形式

邻接矩阵

无权有向图：出度=i行之和；入度：j列之和
加权邻接矩阵：相连为W，不相连为∞

邻接表

用顶点数组和边表表示图
顶点数组用于存放所有顶点
边表用于记录边的数据和指向点

遍历方式

深度遍历：又称DFS算法，利用堆栈
广度遍历：又称BFS算法，利用队列

求解最短路径

Dijkstra算法：求解一个顶点到其他顶点的最短路径
Floyd算法：求解所有顶点到除自己外的顶点的最短路径

疑难问题及解决方案

问题：如何使Floyd算法在代码上基于Dijkstra算法进行实现
解决方案：在Dijkstra函数在定义一个bool变量，
if(TF == true)//用于Floyd算法
{
for (j = 0; P[j]; j++)//循环得到的Path表
{
if (j == i)//当前顶点==当前Path表元素下标
{
P[0][j] = -1;
}
}
}
再在Floyd函数中循环顶点，将通过Dijkstra算法获得的一维数组Path表赋予二维数组Path表
不过算法时间的复杂度还是只能优化到O（n^3），不过Floyd算法代码长度倒是减短了