[QOJ 8366] 火车旅行

毒瘤边化点，有人说非排列只需要加一些细节，但是这个题毒瘤在于非排列。

statement

给定一个长度为 \(n\) 的序列 \(a_i\)。

对于位置 \(x\) 和 \(y\)：

• 若 \(y < x\) 且 \(max_{y < i < x} a_i < min(a_x, a_y)\) 则位于 \(x\) 的棋子可以花费 \(L_x\) 的代价跳到 \(y\)。
• 若 \(y > x\) 且 \(max_{x < i < y} a_i < min(a_x, a_y)\) 则位于 \(x\) 的棋子可以花费 \(R_x\) 的代价跳到 \(y\)。

\(L_i\) 非严格单调递增，\(R_i\) 非严格单调递减。

\(q\) 组询问，每次给定 \(s\) 和 \(t\)，求一枚棋子从 \(x\) 跳到 \(y\) 的最小代价。

多测，\(\sum n, \sum q \le 3 \times 10^5\)。

solution

直接最短路 \(O(n^2\log n)\)，可以获得 38 pts 的好成绩。

跳棋子问题考虑倍增。

手玩一些样例可以发现，最优解起点到终点路径的高度，有一段非严格单调递增，可能经过一段平台期后，有一段非严格单调递减。

于是只可能跳到中间最大的，或者两边最近的比这个中间最大的数还要大的。

后一段可以逆着做，当成非严格单增。

在 \(0\) 和 \(n+1\) 的位置建立 \(a_i = +\infty\) 的哨兵节点。

设 \(pre_x\) 为 \(x\) 前第一个 \(a_y \ge a_x\) 的 \(y\)，\(nxt_x\) 为 \(x\) 后第一个 \(a_y \ge a_x\) 的 \(y\)。\(pre\) 和 \(nxt\) 构成树形结构。

那么 \(x\) 向上跳到某个目标的高位点，必然是经过 \(pre_x\) 和 \(nxt_x\) 中的一部分。考虑边化点之后倍增。

建边 \((pre_x, x) \rightarrow (pre_x, nxt_x)\)，\((x, nxt_x) \rightarrow (pre_x, nxt_x)\)。

对于边 \((a, b) \rightarrow (c, d)\)，边权为向量 \(( dis(x, a)\ dis(x, b) )\) 转移到 \(( dis(x, c)\ dis(x, d) )\) 的 \((\min, +)\) 转移矩阵。

如果出现一段平的（若干个相等的数中间没有更大的），那么建一个节点，它的左端点为平段的起点，右端点为平段的终点，内部的向它连边。

平段内的节点记录向左/右的前/后缀和，注意此时转移边的细节。

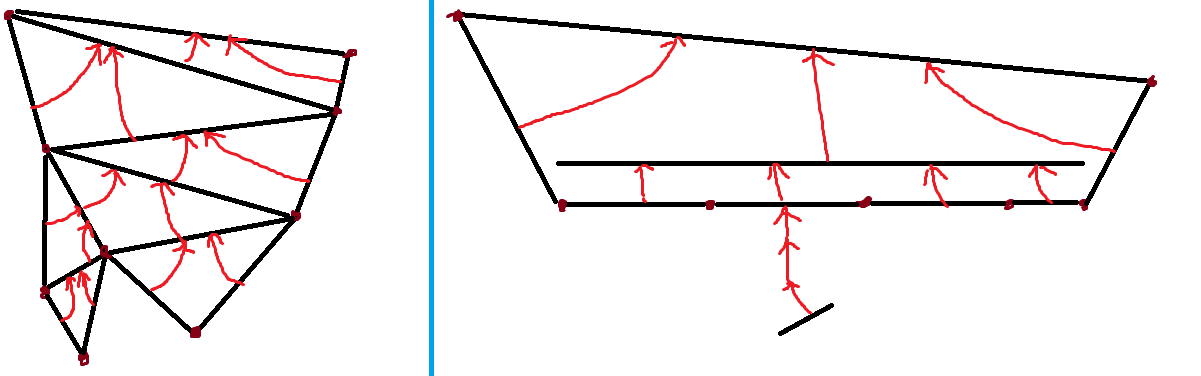
跳的时候，确定目标高度后，一个节点可以向左或者向右跳到离他最近的这一高度的位置。然后同一层的使用前缀和来算。