[深度搜索]n 皇后问题简单做法

八皇后问题

代码

#include <iostream>
using namespace std;

const int N = 14;
int n;
bool col[N], dg[2*N], udg[2*N];
char g[N][N];
int count = 0;
int solve = 0;

inline void dfs(int u) {
	if (u == n) {
		count ++;
		if (solve++ < 3) {
			for (int i = 0; i < n; i++) {
				for (int j = 0; j < n; j++) {
					if (g[i][j] == 'Q') {
						cout << j + 1 << ' ';
					}
				}
			}
			puts("");
		}


		return;
	}

	for (int i = 0; i < n; i++) {
		if (!col[i] && !dg[u + i] && !udg[i - u + n]) {
			col[i] = dg[u + i] = udg[i - u + n] = true;
			g[u][i] = 'Q';
			dfs(u + 1);
			g[u][i] = '.';
			col[i] = dg[u + i] = udg[i - u + n] = false;
		}
	}
}

int main() {
	cin >> n;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			g[i][j] = '.';
		}
	}
	dfs(0);
	cout << count << endl;
}

1.预处理部分

### 变量预处理部分
const int N = 14;
int n;
bool col[N], dg[2*N], udg[2*N];
char g[N][N];
int count = 0;
int solve = 0;

• 测试数据中 n 最大不超过 13
• n: 表示棋盘的大小 n x n
• col: 表示列上是否存在皇后
• dg: 表示一个正对角线上是否存在皇后
• udg: 表示一个反对角线上是否存在皇后
• count: 统计答案总数
• solve: 统计已经输出的答案，方便只输出前三个

cin >> n;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			g[i][j] = '.';
		}
	}

• 初始化棋盘为.表示没有落子的状态

2.搜索皇后部分

inline void dfs(int u) {
	if (u == n) {
		count ++;
		if (solve++ < 3) {
			for (int i = 0; i < n; i++) {
				for (int j = 0; j < n; j++) {
					if (g[i][j] == 'Q') {
						cout << j + 1 << ' ';
					}
				}
			}
			puts("");
		}


		return;
	}

	for (int i = 0; i < n; i++) {
		if (!col[i] && !dg[u + i] && !udg[i - u + n]) {
			col[i] = dg[u + i] = udg[i - u + n] = true;
			g[u][i] = 'Q';
			dfs(u + 1);
			g[u][i] = '.';
			col[i] = dg[u + i] = udg[i - u + n] = false;
		}
	}
}

众所周知，搜索问题可以看作一颗树。

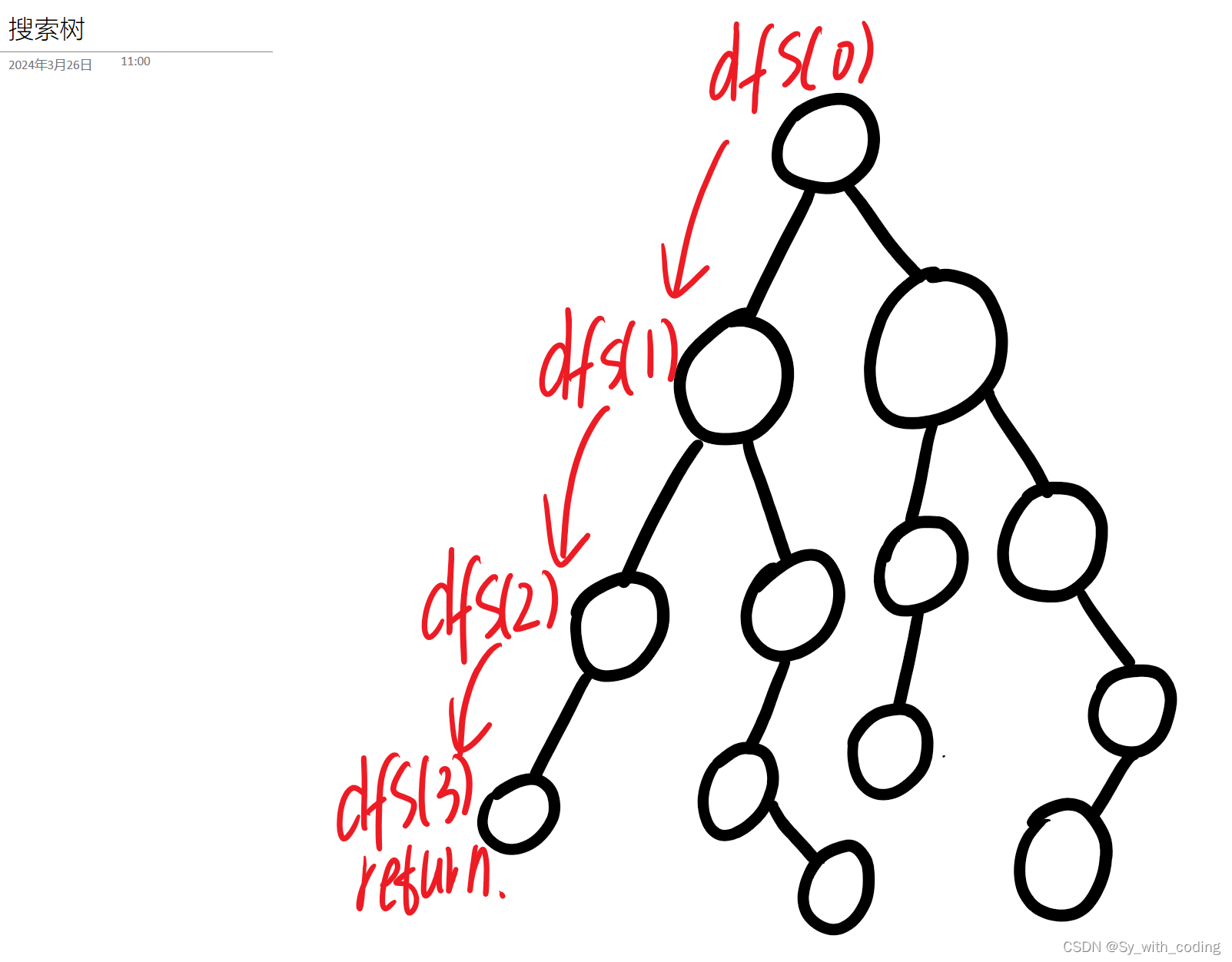
总的来说就是，没有递归到最深处，也就是没有返回的情况，就会进行深度优先遍历，一头扎到死。

所以每一次都只会处理一颗子树。我们回溯的时候将变量恢复成原来的样子，也就是‘恢复现场’，方便进行下一次处理。

表现为代码就是

for (int i = 0; i < n; i++) {
		if (!col[i] && !dg[u + i] && !udg[i - u + n]) {
			col[i] = dg[u + i] = udg[i - u + n] = true;
			g[u][i] = 'Q';
			dfs(u + 1);
			g[u][i] = '.';
			col[i] = dg[u + i] = udg[i - u + n] = false;
		}
	}

这个代码干了什么：

• 对于递归的每一行 u
• 遍历 每一列i : 0 ~ n
• 如果这一列没有皇后，两个对角线没有皇后
• 将这一列以及两个对角线设置成true表示有皇后，更新地图
• 进入下一层
• 回溯的时候当然是从dfs(u + 1)里面跳出来
• ‘恢复现场’即可