3分钟教你弄懂【01背包问题】

背包问题

推荐一个手动运行01背包问题的网站

一步一步手动执行01背包

介绍

将有限物品按找最大价值装进有限体积的背包中去

核心步骤

1.确定状态表示
2.确定边界和遍历顺序
3.找到状态转移方程

先上 Coding

#include <iostream>
using namespace std;

const int N = 300;
int itemSize[N];			//每件物品的大小（体积）
int itemValue[N]; 			//每件物品的价值
int dp[N][N];				//状态表示数组（[物品序号][背包大小]）
int m, n;					//m为背包体积 n为物品数量

int main() {
	cin >> m >> n;

	for (int i = 1; i <= n; i++) {
		cin >> itemSize[i] >> itemValue[i];
		//依次输入每一件物品的体积和价值
	}

	 for (int i = 1; i <= n; i++) {						//n物品数量
		for (int j = 1; j <= m; j++) { 					//m为背包体积
			if (itemSize[i] <= j) {
				//物品体积比j（背包容量）小，可以放进背包，取放和不妨两种情况价值Value的最大值
				dp[i][j] = max(dp[i-1][j], dp[i-1][j-itemSize[i]] + itemValue[i]);
			}
			else {
				//放不进去的情况
				dp[i][j] = dp[i-1][j];
			}
		}
	}

	cout << "dp数组:" << endl;
	for (int i = 0; i <= n; i++) {
		for (int j = 0; j <= m; j++) {
			cout << dp[i][j] << ' ';
		}cout << endl;
	}
}

手动遍历的结果

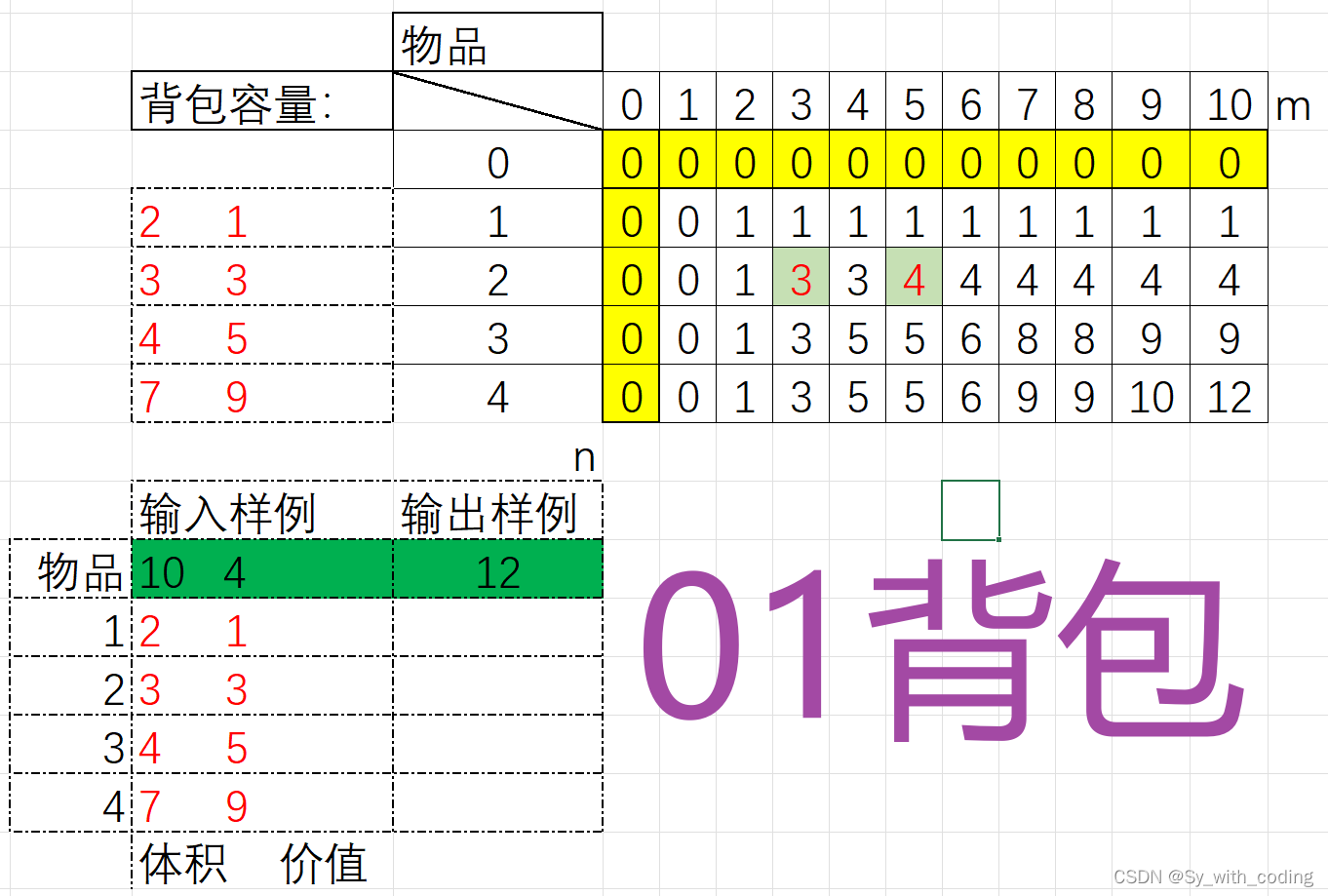
思路

1. 首先遍历每一个物品
2. 对每一个物品，遍历背包的大小
   对于每一种物品都有两种情况

• 当前所遍历的背包大小放得下
• 当前所遍历的背包大小放不下

  注意这里的背包指的是我们分解出来的子状态中的，是对于每一个物品，从0 ~ m（背包的大小），遍历了m+1个背包中的任意一种。

状态表示

dp[i][j]

• i：表示从第1个物品到i个物品这个范围
• j：表示背包大小的一种可能性

边界

满足i==0 && j==0设置为 0

遍历顺序

遍历1~n个物品，对每个物品遍历背包大小

状态转移方程

• 如果拿不下

  dp[i][j] = dp[i-1][j]

• 如果拿得下

  dp[i][j] = max(dp[ i - 1 ][ j ], dp[ i - 1 ] j-size[i]] + value[i])

解释一下这个转移方程中 max 内的两个参数:

• dp[i-1][j] 表示这个除去这个物品(第 i 位物品)以外的0 ~ i-1个物品，也就是拿得下，但是你就是不拿这个物品的情况
• dp[i-1][j - size[i]] + value[i]：这个式子由两个式子相加得来，左边的i-1依旧表示这个物品不拿，0 ~ i-1个物品的情况，j - size[i]表示拿了这个物品之后，剔除这个物品的背包大小的最优解，value[i]就表示这个物品的价值

剥离出来就是

• dp[i-1][j]：除去这个物品，对应背包大小的最优解
• j - size[i]：剔除这个物品的背包大小的最优解
• value[i]：这个物品的价值