[力扣DP]72. 编辑距离

LeetCode 编辑距离

题目描述

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

示例 1：

输入：word1 = “horse”, word2 = “ros”
输出：3
解释：
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)
示例 2：

输入：word1 = “intention”, word2 = “execution”
输出：5
解释：
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)

提示：
0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成

LeetCode 原题链接

参考思路

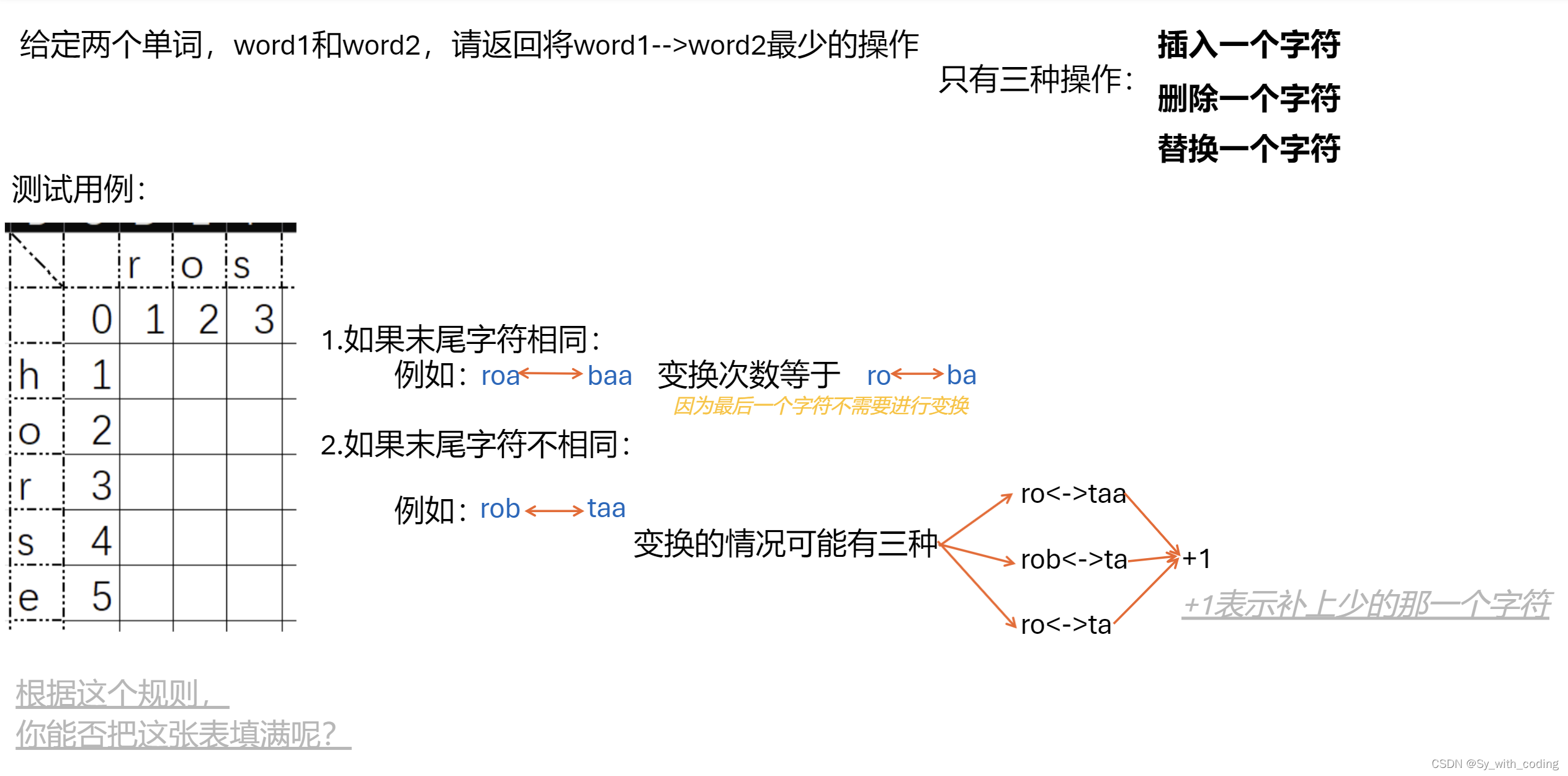
状态表示

dp[i][j] 表示单词1的前i个字母 <–> 单词2的前j个字母的最小路径

动态转移方程

if (word1[i] == word2[j]) {
    dp[i][j] = dp[i-1][j-1];
} else if (word1[i] != word2[j]) {
    dp[i][j] = min({dp[i-1][j-1], dp[i-1][j], dp[i][j-1]}) + 1;
}

边界设置

在dp中的索引为0表示空字符

代码

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.length(), n = word2.length();
        int dp[m+1][n+1];
        for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
                if (i == 0) {
                    dp[i][j] = j;
                } else if (j == 0) {
                    dp[i][j] = i;
                } else if (word1[i-1] == word2[j-1]) {
                    dp[i][j] = dp[i-1][j-1];
                } else if (word1[i-1] != word2[j-1]) {
                    dp[i][j] = min({dp[i-1][j-1], dp[i-1][j], dp[i][j-1]}) + 1;
                }
            }
        }
        for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
                cout << dp[i][j] << ' ';
            }cout << endl;
        }
        return dp[m][n];
    }
};