快速排序算法

快速排序算法

快排算法与归并算法同样是采用的分治的思想，而归并的重点在于归并，快排的重点就在于划分，所以partition算法就很重要，也是很多题目解题的关键

快速排序的基本思想是任取待排序序列的一个元素作为中心元素(可以用第一个，最后一个，也可以是中间任何一个)，习惯将其称为pivot，将所有比枢轴元素小的放在其左边；将所有比它大的放在其右边；
形成左右两个子表；然后对左右两个子表再按照前面的算法进行排序，直到每个子表的元素只剩下一个。

所以快排的算法的递归壳子为：

public static void quickSort(int[] nums) {
    if (nums == null || nums.length < 2) {
        return;
    }
    quickSort(nums, 0, nums.length - 1);
}

public static void quickSort(int[] nums, int start, int end) {
    if (start==end||start>end){
        return;
    }
    //随机取一个数为pivot
    int pivot = start + (int)((end - start + 1) * Math.random());
    swap(nums,pivot,end);
    int[] part = partition(nums,start,end);
    quickSort(nums,start,part[0]-1);
    quickSort(nums,part[1]+1,end );
}

partition算法：

1. 使得数组的最后一个值作为piovt
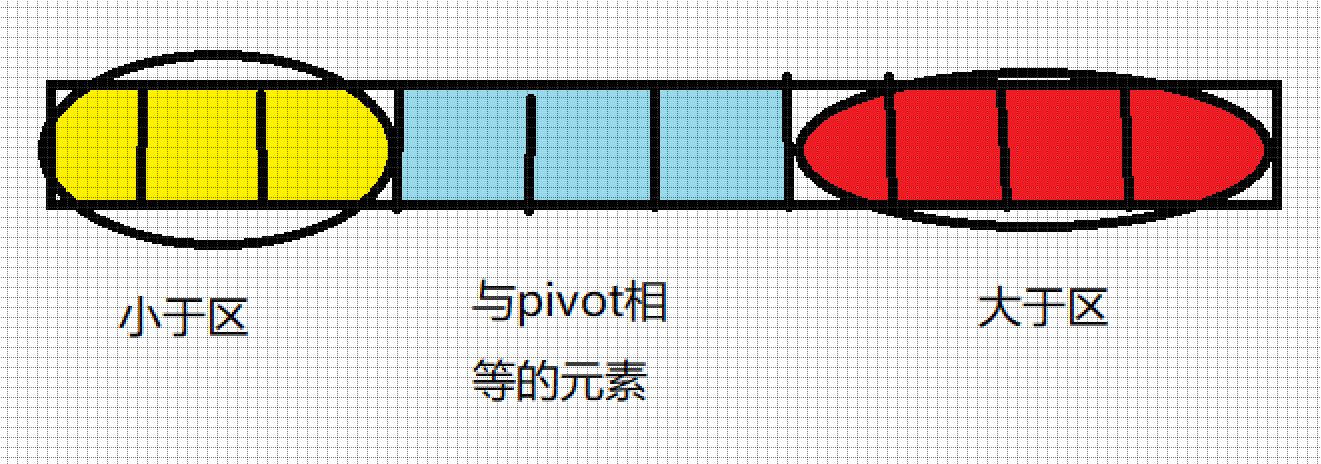
2. 建立小于区，初始位置在数组0位置后面，大于区为数组右边包含piovt，方便比较。
3. 当i值小于piovt时，将i值与小于区前的一个元素交换位置，小于区再向右方扩展一个位置，i++；
4. 当i值等于piovt时，i++；
5. 当i值大于piovt时，将i值与大于区前的一个元素交换位置，大于区再向左方扩展一个位置；
6. 最后当i与大于区相邻时，将piovt与max元素交换，就完成了

partition算法的代码如下：

public static int[] partition(int[] nums,int start,int end){
        int min = start-1;//小于区
        int max = end;//大于区
        int i=start;
        while(i<max){
            if (nums[i]<nums[end]){
                swap(nums,i++,++min);
            }else if (nums[i]>nums[end]){
                swap(nums,i,--max);
            }else{
                i++;
            }
        }